The limit properties diffusion process in a semi-Markov environment
Yaroslav Chabanyuk
,Wojciech Rosa
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE LIMIT PROPERTIES DIFFUSION PROCESS IN A SEMI-MARKOV ENVIRONMENT
Yaroslav Chabanyuk, Wojciech Rosa
Department of Applied Mathematics Lublin
University of Technology
Lublin, Poland
y.chabanyuk@pollub.pl, w.rosa@pollub.pl
Received: 20 December 2017;
Accepted: 23 February 2018
Abstract. In this paper we consider the stochastic diffusion process with semi-Markov switchings in an averaging scheme. We present results and conditions on convergence to the classic diffusion process, in case with semi-Markov process perturbation is uniformly ergodic. We used small parameter scheme to get the main result.
MSC 2010: 60F05, 60J60, 60J70, 93E20.
Keywords: stochastic approximation procedure, compensating operator, asymptotic normality of the stochastic procedure, small parameter, martingale characterization, Markov and semi-Markov processes
1. Introduction
Due to the wide use of stochastic diffusion processes, stability problem arose, especially conditions of stability and control of such systems. The paper [1] contains sufficient conditions of stability of stochastic systems via Lyapunov function properties and obtained estimates of large deviations of linear diffusion systems. Problems of optimal control of diffusion processes are described by stochastic differential equations with acceptable control of dedicated work [2]. This generator uses a diffusion process, Markov property and martingale characterization of the process to test the functions of the Lyapunov type.
On the other hand, asymptotic behavior is important of diffusion processes that are considered in [3] and [4]. For conditions of weak convergence of random processes in the works [5-7] Korolyuk used method of small parameter and singular perturbation problem solution for the construction of the generator limiting process. This method is used in the schemes averaging diffusion approximation and asymptotically small diffusion. In particular in the work [6] Korolyuk and Limnios examined cases of the random evolution of Markov and semi-Markov switching.
Construction of semi-Markov processes and investigation of asymptotic properties of random processes with semi-Markov switching are devoted [8-11].
The initial process is weakly convergent to the solution of the diffusion equation (to the diffusion process). Such convergence is obtained by using averaging scheme [10, 12].
Note [13] work which analyzed the asymptotic properties of semi-Markov processes with a linearly perturbed operator maintainer Markov process through the semi-group property. The latest results were developed in [14]. Classification of solving of the singular perturbation problem for random processes with semi-Markov switching is described at [6] and [15] using of compensating the operator [16]. Through compensating the operator [17] one could obtain sufficient conditions for stability of random evolution of semi-Markov switching to the diffusion process in the balance sheet and the scheme averaging [18].
The results of these studies have been used in various applications [19-22].
2. Problem
In this paper, we consider dynamical system
with semi-Markov switching using a
small series parameter. ![]() is a semi-Markov process in the
standard phase space of states
is a semi-Markov process in the
standard phase space of states ![]() generated by renewal Markov process
generated by renewal Markov process ![]() defined by a semi-Markov kernel:
defined by a semi-Markov kernel:
where the stochastic kernel
defines an embedded Markov chain ![]() at renewal moments:
at renewal moments:
with
intervals ![]() between renewal moments.
between renewal moments. ![]() are defined by the distribution functions
are defined by the distribution functions
A semi-Markov process is defined by the relation
where the counting process ![]() is defined by the formula:
is defined by the formula:
We
consider a semi-Markov process ![]() that is regular and uniformly ergodic
with stationary distribution
that is regular and uniformly ergodic
with stationary distribution ![]()
Here ![]() is a stationary distribution of the Markov chain attached.
is a stationary distribution of the Markov chain attached.
Diffusion process ![]() in an averaging scheme with a
small parameter
in an averaging scheme with a
small parameter ![]() defined by stochastic
differential equation
defined by stochastic
differential equation
| (1) |
where: ![]() -
random evolution in a diffusion process (1) [6, 9, 15, 16];
-
random evolution in a diffusion process (1) [6, 9, 15, 16];
![]() - semi-Markov
process [6, 8, 13, 14];
- semi-Markov
process [6, 8, 13, 14];
![]() - Wiener process
[3-5].
- Wiener process
[3-5].
Semigroup ![]() accompanying
systems
accompanying
systems
| (2) |
defined by the relation
| (3) |
where
| (4) |
and (4) is semigroup property.
Generating operator ![]() semigroup
semigroup
![]() is defined by form
is defined by form
| (5) |
where ![]()
3. Main result
Theorem
1. Let
regression function ![]() and variation
and variation ![]() satisfy the follow-
ing conditions:
satisfy the follow-
ing conditions:
C1: ![]() ,
,
C2: ![]() ,
,
C3: the distribution
functions ![]() satisfy
the Cramer condition uniformly in
satisfy
the Cramer condition uniformly in ![]() ,
,
Then
the solution ![]() of the equation (1) converges weakly to the limit diffusion
process
of the equation (1) converges weakly to the limit diffusion
process ![]() as
as ![]() which is defined by the generator
which is defined by the generator
where
4. Limit operator properties
We introduce advanced Markov renewal process (MRP) [6], by given sequence:
| (6) |
Where ![]() means times of renewal in semi-Markov process
means times of renewal in semi-Markov process ![]() [6] determined by
the distribution function of the time spent in the state x.
[6] determined by
the distribution function of the time spent in the state x.
Definition 1. [6, 17] Compensating operator advanced MRP (6) is defined by the form
| (7) |
Lemma 1. Compensating operator (7) on test-functions ![]() is defined by
formula:
is defined by
formula:
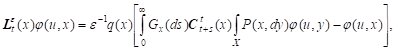 | (8) |
where
Proof. Given point ![]() we
have [6, 16, 18]:
we
have [6, 16, 18]:
Here we have (8).
Lemma 2. Compensating
operator ![]() is defined by form
is defined by form
| (9) |
where ![]()
Proof. From (8) we have
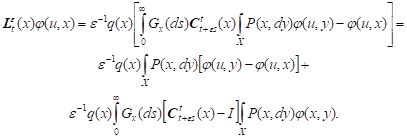 |
Then we obtain (9).
Lemma 3.
Compensating operator ![]() has the asymptotic
representation
has the asymptotic
representation
| (10) |
| (11) |
where
and
where
Proof. We have semigroup equation ![]()
Integrating by parts we have:
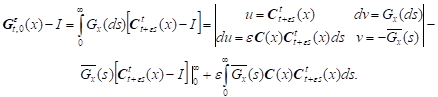 |
Given the Cramer condition we have:
Hence we have (10).
For
integrating by parts we have:
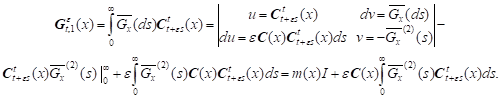 |
Thus we have
Hence:
and
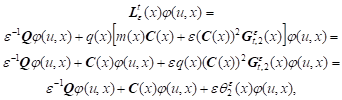 |
where
Lemma 4. Compensating operator ![]() has the asymptotic representation in the function
has the asymptotic representation in the function ![]()
where
Proof. We have
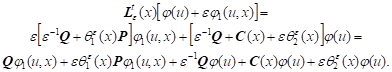 |
Lemma 5. The
given singular perturbation problem [6, 15, 19], limit generator ![]() is defined by formula:
is defined by formula:
Proof. From [6, 19] ![]() we have
we have
Using formula from lemma 3 we have:
where
Hence
| (12) |
Now using statement [6] we get lemma 5.
5. Proof of theorem
Use the following theorem
Theorem. [6] (Pattern limit theorem) If the following conditions holds:
(C1): The
family of embedded Markov renewal process ![]() is rela-
tively compact.
is rela-
tively compact.
(C2): There exists a family of test functions
![]() in
in ![]() , such that
, such that
uniformly on ![]()
(C3): The following convergence holds
uniformly
on ![]() The family of functions
The family of functions ![]() is uniformly bounded and
is uniformly bounded and ![]() and
and ![]() belong to
belong to ![]() .
.
(C4): The convergence of the initial values holds, that is,
and
Then
the weak convergence ![]() takes place. The limit process
takes place. The limit process ![]() with generator
with generator ![]() and is characterized by the
martingale:
and is characterized by the
martingale:
Proof of theorem 1.
Performance conditions (C1) arise from [17]. Performance conditions (C2) arise from ![]() and (12). Performance conditions (C3) arise
from lemma 3 and
lemma 5. It must
show boundaries of
and (12). Performance conditions (C3) arise
from lemma 3 and
lemma 5. It must
show boundaries of ![]() . Consider
. Consider ![]() .
.
With
bounded operators ![]() [3, 5] and sleekness by function
[3, 5] and sleekness by function ![]() followed the limited
followed the limited ![]() . This gives us bound of
. This gives us bound of ![]() .
.
Performance conditions (C4) arise from [15].
Thus we get the assertion of Theorem 1.
Corollary
1. The
diffusion process ![]() is the solution of the stochastic
differential equation:
is the solution of the stochastic
differential equation:
The same result can be obtained for the similar process:
Theorem 2. Let
regression function ![]() and variation
and variation ![]() satisfy the follow-
ing conditions:
satisfy the follow-
ing conditions:
C1: ![]() ,
,
C2: ![]() ,
,
C3: the distribution functions ![]() satisfy
the Cramer condition uniformly in
satisfy
the Cramer condition uniformly in ![]() ,
,
Then the solution ![]() of the equation
of the equation
converges
weakly to the limit diffusion process ![]() as
as ![]() which is
defined by the generator
which is
defined by the generator
where
6. Conclusions
Sufficient conditions were obtained for the convergence of the diffusion process with semi-Markov switching to the classical diffusion process. Two cases were considered here: when the variance is independent of the semi-Markov switching process and when the variance depends on this process. In order to obtain results, the distribution properties are crucial, especially Cramer’s condition. Limit process is an asymptotic approximation of the initial process in the sense of a probabilistic approach. The converge conditions are simple and their determination can be implemented in a computer program. This result can be used in the Poisson Approximation scheme [21-23] for the diffusion process with semi-Markov switching.
References
[1] Blankenship, G.L., & Papanicolaou, G.C. (1978). Stability and control of stochastic systems with wide band noise disturbances. SIAM. Appl. Math, 34, 437-476.
[2] Kushner, H.J. (1978). Optimality conditions for the average cost per unit time problem with a diffusion model. Siam J. Control and Optimization, 16, 2, 330-346.
[3] Skorokhod, A.V. (1989). Asymptotic Methods in the Theory of Stochastic Differential Equations. AMS, 78, Providence.
[4] Stroock, D.W., & Varadhan, S.R.S. (1979). Multidimensional Diffusion Processes. Berlin: Springer- Verlag.
[5] Korolyuk, V.S. (1998). Stability of stochastic systems in the diffusion approximation scheme. Ukrainian Mathematical Journal, 50, 40-54.
[6] Korolyuk, V.S., & Limnios, N. (2005). Stochastic Systems in Merging Phase Space. Singapore: World Scientific.
[7] Korolyuk, V.S. (2010). Problem of large deviations for Markov random evolutions with independent increments in the scheme of asymptotically small. Ukrainian Mathematical Journal, 62, 739-747.
[8] Anisimov, V.V. (1978). Limit theorems for switching processes and their applications. Cybernetics, 14(6), 917-929.
[9] Anisimov, V.V. (1988). Limit theorems for switching processes. Theory Probab. and Math. Statist., 37, 1-5.
[10] Anisimov, V.V. (1995). Switching processes: Averaging principle, diffusion approximation and applications. Acta Applicandae Mathematicae, 40, 95-141.
[11] Anisimov, V.V. (1999). Averaging methods for transient regimes in overloading retrial queuing systems. Mathematical and Computing Modelling, 30(3/4), 65-78.
[12] Anisimov, V.V. (2008). Switching Processes in Queueing Models. London: Wiley, Sons, ISTE.
[13] Korolyuk, V.S., & Swishchuk, A.V. (1994). Random Evolutions. Dordrecht: Kluwer Acad. Publ.
[14] Korolyuk, V.S., & Korolyuk, V.V. (1999). Stochastic Models of Systems. Dordrecht: Kluwer.
[15] Korolyuk, V.S., Korolyuk, V.V., & Limnios, N. (2009). Queueing systems with semi-Markov flow in average and diffusion approximation schemes. Methodol. Comput. Appl. Probab., 11, 201-209.
[16] Sviridenko, M.N. (1986). Martingale approach to limit theorems for semi-Markov processes. Theor. Probab. Appl., 540-545.
[17] Chabanyuk, Ya.M. (2007). Stability of a dynamical system with semi-Markov switchings under conditions of diffusion approximation. Ukrainian Mathematical Journal, 59, 1441-1452.
[18] Korolyuk, V.S., & Chabanyuk, Ya.M. (2002). Stability of a dynamical system with semi-Markov switchings under conditions of stability of the averaged system. Ukrainian Mathematical Journal, 54, 239-252.
[19] Chabanyuk, Ya.M. (2007). Continuous stochastic approximation with semi-Markov switchings in the diffusion approximation scheme. Cybernetics and Systems Analysis, 43, 605-612.
[20] Chabanyuk, Ya.M. (2007). Convergence of a jump procedure in a semi-Markov environment in diffusion-approximation scheme. Cybernetics and Systems Analysis, 43, 866-875.
[21] Korolyuk, V.S., Limnios, N., & Samoilenko, I.V. (2011). Poisson aproximation of recurent process with semi-Markov switching. Stochastic Analisys and Applications, 29, 769-778.
[22] Korolyuk, V.S., Limnios, N., & Samoilenko, I.V. (2010). Poisson aproximation of recurent process with locally independent increments and semi-Markov switching - toward application in reliability. Advances in Degradation Modeling, January, 105-116.
[23] Samoilenko, I.V., Chabanyuk, Y.M., Nikitin, A.V., & Khimka, U.T. (2017). Differential equations with small stochastic additions under poisson approximation conditions. Cybernetics and Systems Analysis, 53, 3, 410-416.

