The limit properties diffusion process in a semi-Markov environment

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Chabanyuk_2018,
   doi = {10.17512/jamcm.2018.1.01},
   url = {https://doi.org/10.17512/jamcm.2018.1.01},
   year = 2018,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {17},
   number = {1},
   pages = {5--14},
   author = {Yaroslav Chabanyuk and  Wojciech Rosa},
   title = {The limit properties diffusion process in a semi-Markov environment},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2018.1.01
UR  - https://doi.org/10.17512/jamcm.2018.1.01
TI  - The limit properties diffusion process in a semi-Markov environment
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Chabanyuk, Yaroslav
AU  - Rosa, Wojciech
PY  - 2018
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 5
EP  - 14
IS  - 1
VL  - 17
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Chabanyuk, Y., & Rosa, W. (2018). The limit properties diffusion process in a semi-Markov environment. Journal of Applied Mathematics and Computational Mechanics, 17(1), 5-14. doi:10.17512/jamcm.2018.1.01

Chabanyuk, Y. & Rosa, W., 2018. The limit properties diffusion process in a semi-Markov environment. Journal of Applied Mathematics and Computational Mechanics, 17(1), pp.5-14. Available at: https://doi.org/10.17512/jamcm.2018.1.01

[1]Y. Chabanyuk and W. Rosa, "The limit properties diffusion process in a semi-Markov environment," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 1, pp. 5-14, 2018.

Chabanyuk, Yaroslav, and Wojciech Rosa. "The limit properties diffusion process in a semi-Markov environment." Journal of Applied Mathematics and Computational Mechanics 17.1 (2018): 5-14. CrossRef. Web.

1. Chabanyuk Y, Rosa W. The limit properties diffusion process in a semi-Markov environment. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(1):5-14. Available from: https://doi.org/10.17512/jamcm.2018.1.01

Chabanyuk, Yaroslav, and Wojciech Rosa. "The limit properties diffusion process in a semi-Markov environment." Journal of Applied Mathematics and Computational Mechanics 17, no. 1 (2018): 5-14. doi:10.17512/jamcm.2018.1.01

THE LIMIT PROPERTIES DIFFUSION PROCESS IN A SEMI-MARKOV ENVIRONMENT

Yaroslav Chabanyuk, Wojciech Rosa

Department of Applied Mathematics Lublin University of Technology
Lublin, Poland
y.chabanyuk@pollub.pl, w.rosa@pollub.pl

Received: 20 December 2017; Accepted: 23 February 2018

Abstract. In this paper we consider the stochastic diffusion process with semi-Markov switchings in an averaging scheme. We present results and conditions on convergence to the classic diffusion process, in case with semi-Markov process perturbation is uniformly ergodic. We used small parameter scheme to get the main result.

MSC 2010: 60F05, 60J60, 60J70, 93E20.

Keywords: stochastic approximation procedure, compensating operator, asymptotic normality of the stochastic procedure, small parameter, martingale characterization, Markov and semi-Markov processes

1. Introduction

Due to the wide use of stochastic diffusion processes, stability problem arose, especially conditions of stability and control of such systems. The paper [1] contains sufficient conditions of stability of stochastic systems via Lyapunov function properties and obtained estimates of large deviations of linear diffusion systems. Problems of optimal control of diffusion processes are described by stochastic differential equations with acceptable control of dedicated work [2]. This generator uses a diffusion process, Markov property and martingale characterization of the process to test the functions of the Lyapunov type.

On the other hand, asymptotic behavior is important of diffusion processes that are considered in [3] and [4]. For conditions of weak convergence of random processes in the works [5-7] Korolyuk used method of small parameter and singular perturbation problem solution for the construction of the generator limiting process. This method is used in the schemes averaging diffusion approximation and asymptotically small diffusion. In particular in the work [6] Korolyuk and Limnios examined cases of the random evolution of Markov and semi-Markov switching.

Construction of semi-Markov processes and investigation of asymptotic properties of random processes with semi-Markov switching are devoted [8-11].

The initial process is weakly convergent to the solution of the diffusion equation (to the diffusion process). Such convergence is obtained by using averaging scheme [10, 12].

Note [13] work which analyzed the asymptotic properties of semi-Markov processes with a linearly perturbed operator maintainer Markov process through the semi-group property. The latest results were developed in [14]. Classification of solving of the singular perturbation problem for random processes with semi-Markov switching is described at [6] and [15] using of compensating the operator [16]. Through compensating the operator [17] one could obtain sufficient conditions for stability of random evolution of semi-Markov switching to the diffusion process in the balance sheet and the scheme averaging [18].

The results of these studies have been used in various applications [19-22].

2. Problem

In this paper, we consider dynamical system with semi-Markov switching using a small series parameter. is a semi-Markov process in the standard phase space of states generated by renewal Markov process defined by a semi-Markov kernel:

where the stochastic kernel

defines an embedded Markov chain at renewal moments:

with intervals between renewal moments. are defined by the distribution functions

A semi-Markov process is defined by the relation

where the counting process is defined by the formula:

We consider a semi-Markov process that is regular and uniformly ergodic with stationary distribution

Here is a stationary distribution of the Markov chain attached.

Diffusion process in an averaging scheme with a small parameter defined by stochastic differential equation

(1)

where: - random evolution in a diffusion process (1) [6, 9, 15, 16];

- semi-Markov process [6, 8, 13, 14];

- Wiener process [3-5].

Semigroup accompanying systems

(2)

defined by the relation

(3)

where

.

(4)

and (4) is semigroup property.

Generating operator semigroup is defined by form

(5)

where

3. Main result

Theorem 1. Let regression function and variation satisfy the follow- ing conditions:

C1: ,

C2: ,

C3: the distribution functions satisfy the Cramer condition uniformly in ,

Then the solution of the equation (1) converges weakly to the limit diffusion process as which is defined by the generator

where

4. Limit operator properties

We introduce advanced Markov renewal process (MRP) [6], by given sequence:

(6)

Where means times of renewal in semi-Markov process [6] determined by the distribution function of the time spent in the state x.

Definition 1. [6, 17] Compensating operator advanced MRP (6) is defined by the form

(7)

Lemma 1. Compensating operator (7) on test-functions is defined by formula:

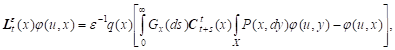(8)

where

Proof. Given point we have [6, 16, 18]:

Here we have (8).

Lemma 2. Compensating operator is defined by form

(9)

where

Proof. From (8) we have

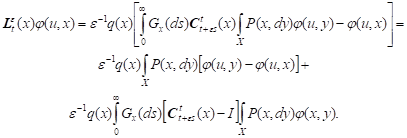Then we obtain (9).

Lemma 3. Compensating operator has the asymptotic representation

(10)

(11)

where

and

where

Proof. We have semigroup equation

Integrating by parts we have:

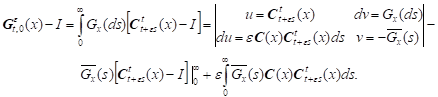Given the Cramer condition we have:

Hence we have (10).

For

integrating by parts we have:

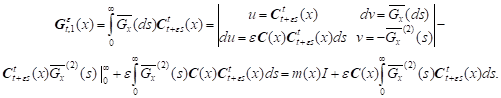Thus we have

Hence:

and

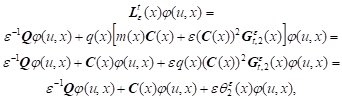where

Lemma 4. Compensating operator has the asymptotic representation in the function

where

Proof. We have

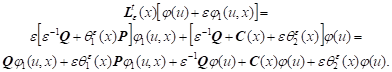Lemma 5. The given singular perturbation problem [6, 15, 19], limit generator is defined by formula:

Proof. From [6, 19] we have

Using formula from lemma 3 we have:

where

Hence

(12)

Now using statement [6] we get lemma 5.

5. Proof of theorem

Use the following theorem

Theorem. [6] (Pattern limit theorem) If the following conditions holds:

(C1): The family of embedded Markov renewal process is rela- tively compact.

(C2): There exists a family of test functions in , such that

uniformly on

(C3): The following convergence holds

uniformly on The family of functions is uniformly bounded and and belong to .

(C4): The convergence of the initial values holds, that is,

and

Then the weak convergence takes place. The limit process with generator and is characterized by the martingale:

Proof of theorem 1.

Performance conditions (C1) arise from [17]. Performance conditions (C2) arise from and (12). Performance conditions (C3) arise from lemma 3 and lemma 5. It must show boundaries of . Consider .

With bounded operators [3, 5] and sleekness by function followed the limited . This gives us bound of .

Performance conditions (C4) arise from [15].

Thus we get the assertion of Theorem 1.

Corollary 1. The diffusion process is the solution of the stochastic differential equation:

The same result can be obtained for the similar process:

Theorem 2. Let regression function and variation satisfy the follow- ing conditions:

C1: ,

C2: ,

C3: the distribution functions satisfy the Cramer condition uniformly in ,

Then the solution of the equation

converges weakly to the limit diffusion process as which is defined by the generator

where

6. Conclusions

Sufficient conditions were obtained for the convergence of the diffusion process with semi-Markov switching to the classical diffusion process. Two cases were considered here: when the variance is independent of the semi-Markov switching process and when the variance depends on this process. In order to obtain results, the distribution properties are crucial, especially Cramer’s condition. Limit process is an asymptotic approximation of the initial process in the sense of a probabilistic approach. The converge conditions are simple and their determination can be implemented in a computer program. This result can be used in the Poisson Approximation scheme [21-23] for the diffusion process with semi-Markov switching.

References

[1] Blankenship, G.L., & Papanicolaou, G.C. (1978). Stability and control of stochastic systems with wide band noise disturbances. SIAM. Appl. Math, 34, 437-476.

[2] Kushner, H.J. (1978). Optimality conditions for the average cost per unit time problem with a diffusion model. Siam J. Control and Optimization, 16, 2, 330-346.

[3] Skorokhod, A.V. (1989). Asymptotic Methods in the Theory of Stochastic Differential Equations. AMS, 78, Providence.

[4] Stroock, D.W., & Varadhan, S.R.S. (1979). Multidimensional Diffusion Processes. Berlin: Springer- Verlag.

[5] Korolyuk, V.S. (1998). Stability of stochastic systems in the diffusion approximation scheme. Ukrainian Mathematical Journal, 50, 40-54.

[6] Korolyuk, V.S., & Limnios, N. (2005). Stochastic Systems in Merging Phase Space. Singapore: World Scientific.

[7] Korolyuk, V.S. (2010). Problem of large deviations for Markov random evolutions with independent increments in the scheme of asymptotically small. Ukrainian Mathematical Journal, 62, 739-747.

[8] Anisimov, V.V. (1978). Limit theorems for switching processes and their applications. Cybernetics, 14(6), 917-929.

[9] Anisimov, V.V. (1988). Limit theorems for switching processes. Theory Probab. and Math. Statist., 37, 1-5.

[10] Anisimov, V.V. (1995). Switching processes: Averaging principle, diffusion approximation and applications. Acta Applicandae Mathematicae, 40, 95-141.

[11] Anisimov, V.V. (1999). Averaging methods for transient regimes in overloading retrial queuing systems. Mathematical and Computing Modelling, 30(3/4), 65-78.

[12] Anisimov, V.V. (2008). Switching Processes in Queueing Models. London: Wiley, Sons, ISTE.

[13] Korolyuk, V.S., & Swishchuk, A.V. (1994). Random Evolutions. Dordrecht: Kluwer Acad. Publ.

[14] Korolyuk, V.S., & Korolyuk, V.V. (1999). Stochastic Models of Systems. Dordrecht: Kluwer.

[15] Korolyuk, V.S., Korolyuk, V.V., & Limnios, N. (2009). Queueing systems with semi-Markov flow in average and diffusion approximation schemes. Methodol. Comput. Appl. Probab., 11, 201-209.

[16] Sviridenko, M.N. (1986). Martingale approach to limit theorems for semi-Markov processes. Theor. Probab. Appl., 540-545.

[17] Chabanyuk, Ya.M. (2007). Stability of a dynamical system with semi-Markov switchings under conditions of diffusion approximation. Ukrainian Mathematical Journal, 59, 1441-1452.

[18] Korolyuk, V.S., & Chabanyuk, Ya.M. (2002). Stability of a dynamical system with semi-Markov switchings under conditions of stability of the averaged system. Ukrainian Mathematical Journal, 54, 239-252.

[19] Chabanyuk, Ya.M. (2007). Continuous stochastic approximation with semi-Markov switchings in the diffusion approximation scheme. Cybernetics and Systems Analysis, 43, 605-612.

[20] Chabanyuk, Ya.M. (2007). Convergence of a jump procedure in a semi-Markov environment in diffusion-approximation scheme. Cybernetics and Systems Analysis, 43, 866-875.

[21] Korolyuk, V.S., Limnios, N., & Samoilenko, I.V. (2011). Poisson aproximation of recurent process with semi-Markov switching. Stochastic Analisys and Applications, 29, 769-778.

[22] Korolyuk, V.S., Limnios, N., & Samoilenko, I.V. (2010). Poisson aproximation of recurent process with locally independent increments and semi-Markov switching - toward application in reliability. Advances in Degradation Modeling, January, 105-116.

[23] Samoilenko, I.V., Chabanyuk, Y.M., Nikitin, A.V., & Khimka, U.T. (2017). Differential equations with small stochastic additions under poisson approximation conditions. Cybernetics and Systems Analysis, 53, 3, 410-416.