O-species and tensor algebras
Nadiya Gubareni
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
O-SPECIES and TENSOR ALGEBRAS
Nadiya Gubareni
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
nadiya.gubareni@yahoo.com
Abstract. In this paper we consider O-species and their representations. These O-species are a type of a generalization of a species introduced by Gabriel. We also consider the tensor algebras of such O-species. It is proved that the category of all representations of an O-species and the category of all right modules over the corresponding tensor algebra are naturally equivalent.
Keywords: species, O-species, representations of O-species, tensor algebra, O-species of bounded representation type, diagram of O-species
1. Introduction
In this paper we consider O-species, which generalize the notion of species introduced by Gabriel in [1]. Recall this definition:
Definition 1.1. (Gabriel [1]). Let I be a finite index set. A species L = (Fi, iMj)i,j Î I is a finite family (Fi)i Î I of division rings together with a family (iMj)i,j Î I of (Fi, Fj)-bimodules.
We say that (Fi, iMj)i,j Î I is a K-species if all Fi are finite dimensional and central over the common commutative subfield K which acts centrally on iMj, i.e. lm = ml for all l Î K and all m Î iMj. We also assume that each bimodule iMj is a finite dimensional vector space over K. K-species is a K-quiver if Fi = K for each i.
Definition 1.2. A representation (Vi, jji) of a species L = (Fi, iMj)i,j Î I (or an L-representation) is a family of right Fi-modules Vi and Fj-linear mappings:
| (1.3) |
for each i, j Î I. Such a representation is called finite dimensional, provided all the spaces Vi are finite dimensional vector spaces.
Let V = (Vi, jji ) and W = (Wi,![]() ) be two L-representations. An L-morphism Y: V ® W is a
set of Fi-linear maps ai : Vi ® Wi such that
) be two L-representations. An L-morphism Y: V ® W is a
set of Fi-linear maps ai : Vi ® Wi such that
| (1.4) |
Two representations (Vi, jji) and W = (Wi, jyi) are called equivalent if there is a set of isomorphisms ai from the Fi-module Vi to the Fi-module Wi such that the (1.4) holds for all i,j Î I.
A representation (Vi, jji) is called indecomposable, if there are no non-zero sets of subspaces (Ui) and (Wi) such that Vi = Ui Å Wi and jji = jyi Å jti , where
| (1.5) |
| (1.6) |
One defines the direct sum of two L-representations in the obvious way.
Denote by Rep(L) the category of all L-representations, and by rep(L) the category of finite dimensional L-representations, whose objects are L-representations and whose morphisms are as defined above.
Definition 1.7. [2] A species L = (Fi, iMj)i,jÎI is said to be of finite type, if the number of indecomposable non-isomorphic finite dimensional representations is finite.
A species L = (Fi, iMj)i,jÎI is said to be of strongly unbounded type if it possesses the following three properties:
1. L has indecomposable objects of arbitrary large finite dimension.
2. If L contains a finite dimensional object with an infinite endomorphism ring, then there is an infinite number of (finite) dimensions d such that, for each d, the species L has infinitely many (non-isomorphic) indecomposable objects of dimension d.
3. L has indecomposable objects of infinite dimension.
Dlab and Ringel proved in [2, Theorem E] that any K-species is either of finite or of strongly unbounded type.
With any species L = (Fi, iMj)i,jÎI one can define the tensor algebra in the
following way. Let ![]() , and let
, and let ![]() . Then B is a ring and M
naturally
becomes a (B, B)-bimodule. The tensor algebra of the
(B, B)-bimodule M is the graded ring
. Then B is a ring and M
naturally
becomes a (B, B)-bimodule. The tensor algebra of the
(B, B)-bimodule M is the graded ring
| (1.8) |
with component-wise addition and the multiplication induced by taking tensor products.
If L is a K-species, then T(L) is a finite dimensional K-algebra.
Theorem 1.9. (Dlab, Ringel [2, Proposition 10.1]). Let L be a K-species. Then the category Rep(L) of all representations of L and the category Modr(T(L)) of all right T(L)-modules are equivalent.
2. O-species and their representations
In this section we consider the notion of O-species, which generalizes the notion of species considered in [1].
Let {Oi} be a family of discrete valuation rings (not necessarily commutative) Oi with radicals Ri and skew fields of fractions Di, for i = 1, 2, ..., k, and let {Dj}, for j = k + 1, ..., n, be a family of skew fields. Let (n1, n2, ..., nk) be a set of natural numbers. Write
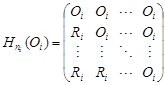 , , |
which is a subring in the matrix ring ![]() . It is easy to
see that each
. It is easy to
see that each ![]() is a Noetherian serial prime hereditary ring. Write Fi =
is a Noetherian serial prime hereditary ring. Write Fi = ![]() for i = 1, 2, ..., k,
and Fj = Dj for j = k + 1,
..., n. Then, by the Goldie theorem, there exists a classical ring of
fractions
for i = 1, 2, ..., k,
and Fj = Dj for j = k + 1,
..., n. Then, by the Goldie theorem, there exists a classical ring of
fractions ![]() for i =1,2, ..., n.
for i =1,2, ..., n.
Consider the following generalization of a species.
Definition 2.1. An O-species is a set W = (Fi, iMj)i,j
Î I, where Fi = ![]() for
i = 1, 2, ..., k, and Fj = Dj
for j = k + 1, ..., n, and moreover iMj
is an
for
i = 1, 2, ..., k, and Fj = Dj
for j = k + 1, ..., n, and moreover iMj
is an ![]() -bimodule, which is finite dimensional
as a right Dj-vector space and as a left
Di -vector space.
-bimodule, which is finite dimensional
as a right Dj-vector space and as a left
Di -vector space.
An O-species W is called a (D, O)-species if all Oi have a common skew field of fractions D, i.e. all Di are equal to a fixed skew field D and
| (2.2) |
for some natural number nij (i = 1, 2, ..., n).
An O-species W is called a (K, O)-species, if all Di (i = 1, 2, ..., n) contain a common central subfield K of finite index in such a way that lm = ml for all l Î K and all m Î iMj (moreover, each bimodule iMj is a finite dimensional vector space over K). It is a (K, O)-quiver if moreover Di = D for each i.
Everywhere in this paper we will consider O-species
without oriented cycles and loops, i.e. we will assume that iMi
= 0, and if iMj ≠ 0, then jMi
= 0. A vertex i
is said to be marked if Fi
= ![]() .
.
We will also assume that all marked vertices
are minimal, i.e. jMi = 0 if
Fi = ![]() , and that iMj
= jMi = 0 if i, j are
marked vertices.
, and that iMj
= jMi = 0 if i, j are
marked vertices.
Definition 2.3. The diagram of an O-species W = {Fi, iMj}i,jÎI is defined in the following way:
1. The set of vertices is a finite set I = {1, 2, ..., n}.
2. The finite subset I0 = {1, 2, ..., k} of I is a set of marked points.
3. The vertex i connects with the vertex j by tij arrows, where
moreover, we assume that ni = 1 if Fi = Di.
Similar to species we can define representations of O-species in the following way.
Definition 2.4. A representation (Mi, Vr, jji, jyr) of an O-species W = {Fi, iMj}i,jÎI is a family of right Fi-modules Mi (i = 1, 2, ..., k), a set of right vector spaces Vr over Dr (r = k +1, k +1, ..., n) and Dj-linear maps:
for each i = 1, 2, ..., k; j = k +1, k +2, ..., n; and
for each r, j = k +1, k +2, ..., n.
Definition 2.5.
Two representations M = (Mi, Vr, jji, jyr) and ![]() are called equivalent if there
is a set of isomorphisms ai of Fi-modules
from Mi to
are called equivalent if there
is a set of isomorphisms ai of Fi-modules
from Mi to ![]() and a set of
isomorphisms br of Dr-vector
spaces from Vr to
and a set of
isomorphisms br of Dr-vector
spaces from Vr to ![]() such
that for each i = 1, 2, ..., k; r, j = k + 1,
k + 2, ..., n the following equalities hold:
such
that for each i = 1, 2, ..., k; r, j = k + 1,
k + 2, ..., n the following equalities hold:
| (2.6) |
| (2.7) |
In a natural way one can define the notions of a direct sum of representations and of an indecomposable representation.
The set of all representations of an O-species
W =
(Fi, iMj)i,jÎI can be turned
into a category R(W), whose objects are representations M = (Mi, Vr, jji, jyr), and
a morphism from object M = (Mi, Vr, jji, jyr) to object ![]() is
a set of homomorphisms ai of
is
a set of homomorphisms ai of ![]() - modules Mi to
- modules Mi to ![]() , and a set of homo-
morphisms br of Dr
- vector spaces from Vr to
, and a set of homo-
morphisms br of Dr
- vector spaces from Vr to ![]() such
that for each i = 1,2, ..., k;
r, j = k + 1, k + 2, ..., n the equalities
(2.6) and (2.7) hold.
such
that for each i = 1,2, ..., k;
r, j = k + 1, k + 2, ..., n the equalities
(2.6) and (2.7) hold.
3. Tensor algebra of O-species
For any O-species W = (Fi, iMj)i,j
Î I one can construct a tensor
algebra of bimodules T(W). Let ![]() ,
, ![]() . Then
B is an (A, A) - bimodule and we can define a tensor
algebra TA(B) of the bimodule B over the ring A
in the following way:
. Then
B is an (A, A) - bimodule and we can define a tensor
algebra TA(B) of the bimodule B over the ring A
in the following way:
| TA(B) = A Å B Å B2 Å ... Å Bn Å ... | (3.1) |
is a graded ring, where Bn = B ÄA Bn‒1 for n > 1, and multiplication in TA(B) is given by the natural A-bilinear map:
| Bn ´ Bm ® Bn ÄA Bm = Bn+m | (3.2) |
Then T(W) = TA(B) is the tensor algebra corresponding to an O-species W.
Proposition 3.3. Let
W be
an O-species. Then the category ![]() (W) of all
representations of W and the category Modr T(W) of all right T(W)-modules are
naturally equivalent.
(W) of all
representations of W and the category Modr T(W) of all right T(W)-modules are
naturally equivalent.
Proof. Form two functors R: Modr T(W) ® ![]() (W) and P:
(W) and P: ![]() (W) ® Modr T(W)
in the following way. Let XT(W) be a right T(W)-module. Since A is a subring
in T(W), X can be considered as a right A-module. Then
(W) ® Modr T(W)
in the following way. Let XT(W) be a right T(W)-module. Since A is a subring
in T(W), X can be considered as a right A-module. Then
| (3.4) |
where Mi
is an ![]() -module, and Vr
is a Dr-vector space; moreover,
-module, and Vr
is a Dr-vector space; moreover, ![]() for i ≠ j, and VrDs
= 0 for r ≠ s. Since B is an (A, A)-bimodule,
one can define an A-homomorphism j : X Ä A B ® XA.
Taking into account that
Mi Ä A sMj = 0 for i
≠ s, the map j is defined in the following way:
for i ≠ j, and VrDs
= 0 for r ≠ s. Since B is an (A, A)-bimodule,
one can define an A-homomorphism j : X Ä A B ® XA.
Taking into account that
Mi Ä A sMj = 0 for i
≠ s, the map j is defined in the following way:
| (3.5) |
Since Mi Ä A iMj is mapping into Vj, and Vr Ä A rMj is mapping into Vj, j defines a set of Dj-homomorphisms:
| (3.6) |
| (3.7) |
for i = 1, 2, ..., k; r, j = k + 1, ..., n.
Now one can define R(XT(W)) = (Mi, Vr, jji, jyr). Let
X, Y be two right
T(W)-modules, let a: X ® Y be a homomorphism, and let R(X) = (Mi,
Vr, jji, jyr), R(Y) = ![]() . Let's define a morphism from R(X) to R(Y).
Since a
is an A-homomorphism, a(Mi) Í Ni,
a(Vr) Í Wr,
i.e., a defines a family of
. Let's define a morphism from R(X) to R(Y).
Since a
is an A-homomorphism, a(Mi) Í Ni,
a(Vr) Í Wr,
i.e., a defines a family of ![]() -homomorphisms ai: Mi ® Ni and a
family of Dr-homomorphisms br:
Vr ® Wr,
which are the restrictions of a to Mi and Vr. Therefore one can
set
R(a) = {(ai), (br)}. Since a is a T(W)-homomorphism,
-homomorphisms ai: Mi ® Ni and a
family of Dr-homomorphisms br:
Vr ® Wr,
which are the restrictions of a to Mi and Vr. Therefore one can
set
R(a) = {(ai), (br)}. Since a is a T(W)-homomorphism,
| (3.8) |
and
| (3.9) |
for i = 1, 2, ..., k; r, j = k + 1, ..., n. Therefore R(a) is a morphism in the category R(W).
Conversely, let W = (Fi, iMj)i,jÎI and there is given a representation M = (Mi, Vr, jji, jyr). Then one can define P(M) in the following way:
| (3.10) |
We define an action of
| (3.11) |
on Mi
by means of the projection A ® ![]() and an action of A on Vr
by means of the projection A ® Dr.
We define an action of Bn on X by induction of
j (n) : X ÄA Bn ® X as follows:
and an action of A on Vr
by means of the projection A ® Dr.
We define an action of Bn on X by induction of
j (n) : X ÄA Bn ® X as follows:
If a = {{ai}, {br}} is a morphism of a
representation M = (Mi, Vr, jji, jyr) to
a representation ![]() , X = P(M),
Y = P(
, X = P(M),
Y = P(![]() ), then
), then
| (3.12) |
is a T(W)-homomorphism and therefore P(a) = j.
It is not difficult to show that R, P
are mutually inverse functors and they give an equivalence of categories Modr
T(W) and ![]() (W).
(W).
Recall that an Artinian ring A is of finite representation type if A has only a finite number of indecomposable finitely generated right A-modules up to isomorphism.
A ring A is of (right) bounded representation type (see [3, 4]) if there is an upper bound on the number of generators required for indecomposable finitely presented right A-modules.
Denote by
m(Mi)
the minimal number of generators of an ![]() -module
Mi, and denote by dr =
-module
Mi, and denote by dr = ![]() the dimension of vector space Vr over Dr.
The dimension of a representation M = (Mi, Vr,
jji, jyr) is the number
the dimension of vector space Vr over Dr.
The dimension of a representation M = (Mi, Vr,
jji, jyr) is the number
| (3.13) |
Definition 3.14. An O-species W is said to be of bounded representation type if the dimensions of its indecomposable finite dimensional representations have an upper bound.
Corollary 3.15. An O-species W is of bounded representation type if and only if the tensor algebra T(W) is of bounded representation type.
Proof. If W is an O-species of bounded representation type, then there exists N > 0 such that dimM < N for any indecomposable finite dimensional representation M. Then for any finitely generated T(W)-module X we have m(X) < N1, where N1 is some fixed number depending on N, i.e. T(W) is a ring of bounded representation type. The converse also holds: if T(W) is a ring of bounded representation type, then W is an O-species of bounded representation type.
Corollary 3.16. Let W1 be a D-species, which is a subspecies of a (D, O)-species W. If W is of bounded representation type, then W1 is of finite type.
Proof. Since W is of bounded representation type, each of its subspecies is of bounded representation type as well. So W1 is of bounded representation type, and, by corollary 3.15, its tensor algebra is of bounded representation type, as well. Since W1 is a D-species, its tensor algebra is an Artinian ring. So it is of finite representation type, by [5]. Therefore, W1 is also of finite representation type.
3. Conclusion
In this paper we introduced O-species and the tensor algebras corresponding to them. These O-species are some generalizations of species first introduced by Gabriel in [1]. We consider the notion of a representation of an O-species. In this paper we prove that the category of all representations of O-species W and the category of all right modules over a tensor algebra T(W) are naturally equivalent.
References
[1] Gabriel P., Indecomposable representations I, Manuscripta Math. 1972, 6, 71-103.
[2] Dlab V., Ringel C.M., On algebras of finite representation type, Journal of Algebra 1975, 33, 306-394.
[3] Warfield R.B., Serial rings and finitely presented modules, Journal of Algebra 1975, 37, 2, 187-222.
[4] Gubareni N., On right hereditary SPSD-rings of bounded representation type I, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 57-70.
[5] Auslander M., Representation theory of Artin algebras II, Comm. Algebra 1974, 1, 269-310.

