About one method of finding expected incomes in HM-queueing network with positive customers and signals
Mikhail Matalytski
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Matalytski_2016,
doi = {10.17512/jamcm.2016.1.09},
url = {https://doi.org/10.17512/jamcm.2016.1.09},
year = 2016,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {15},
number = {1},
pages = {87--98},
author = {Mikhail Matalytski},
title = {About one method of finding expected incomes in HM-queueing network with positive customers and signals},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2016.1.09 UR - https://doi.org/10.17512/jamcm.2016.1.09 TI - About one method of finding expected incomes in HM-queueing network with positive customers and signals T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Matalytski, Mikhail PY - 2016 PB - The Publishing Office of Czestochowa University of Technology SP - 87 EP - 98 IS - 1 VL - 15 SN - 2299-9965 SN - 2353-0588 ER -
Matalytski, M. (2016). About one method of finding expected incomes in HM-queueing network with positive customers and signals. Journal of Applied Mathematics and Computational Mechanics, 15(1), 87-98. doi:10.17512/jamcm.2016.1.09
Matalytski, M., 2016. About one method of finding expected incomes in HM-queueing network with positive customers and signals. Journal of Applied Mathematics and Computational Mechanics, 15(1), pp.87-98. Available at: https://doi.org/10.17512/jamcm.2016.1.09
[1]M. Matalytski, "About one method of finding expected incomes in HM-queueing network with positive customers and signals," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 1, pp. 87-98, 2016.
Matalytski, Mikhail. "About one method of finding expected incomes in HM-queueing network with positive customers and signals." Journal of Applied Mathematics and Computational Mechanics 15.1 (2016): 87-98. CrossRef. Web.
1. Matalytski M. About one method of finding expected incomes in HM-queueing network with positive customers and signals. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(1):87-98. Available from: https://doi.org/10.17512/jamcm.2016.1.09
Matalytski, Mikhail. "About one method of finding expected incomes in HM-queueing network with positive customers and signals." Journal of Applied Mathematics and Computational Mechanics 15, no. 1 (2016): 87-98. doi:10.17512/jamcm.2016.1.09
ABOUT ONE METHOD OF FINDING EXPECTED INCOMES IN HM-QUEUEING NETWORK WITH POSITIVE CUSTOMERS AND SIGNALS
Mikhail Matalytski
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
m.matalytski@gmail.com
Abstract. In the paper an open Markov HM(Howard-Matalytski)-Queueing Network (QN) with incomes, positive customers and signals (G(Gelenbe)-QN with signals) is investigated. The case is researched, when incomes from the transitions between the states of the network are random variables (RV) with given mean values. In the main part of the paper a description is given of G-network with signals and incomes, all kinds of transition probabilities and incomes from the transitions between the states of the network. The method of finding expected incomes of the researched network was proposed, which is based on using of found approximate and exact expressions for the mean values of random incomes. The variances of incomes of queueing systems (QS) was also found. A calculation example, which illustrates the differences of expected incomes of HM-networks with negative customers and QN without them and also with signals, has been given. The practical significance of these results consist of that they can be used at forecasting incomes in computer systems and networks (CSN) taking into account virus penetration into it and also at load control in such networks.
Keywords: HM-queueing network, positive and negative customers, signals, expected incomes, transient regime
1. Introduction
For the first time Markov nets with positive customers and signals were introduced and investigated at the non-stationary behavior by E. Gelenbe, see [1]. The action of the signal consists of instantaneous movement of positive customers of this system to some other network system. The signal may work as a trigger, which doesn’t destroy the customers, but only moves them instantly with a given probability of a given system to another network system.
In developing models of computer viruses we can use negative customers. And for load control in the network can be inputted signals (triggers). When viruses penetrate into computers in the information system, it suffers costs or losses due to the loss of information or CSN distortion. The accounting of the losses in CSN can be realized with the help of a Markov QN model with incomes (HM-networks), positive and negative customers and signals.
In this paper, an open Markov HM-network with positive and negative customers, signals, when the incomes from the transitions between the states of the network are random variables (RV) with time-dependent customer servicing in the systems has been carried out. The expressions for the variances of incomes of queueing systems (QS) was also obtained.
A description of the network is given in [2, 3].
Signal, coming in an empty
system ![]() (in which there are no positive
customers), does not have any impact
on the network and immediately disappeared from it.
Otherwise, if the system
(in which there are no positive
customers), does not have any impact
on the network and immediately disappeared from it.
Otherwise, if the system ![]() is not empty, when it receives a signal, the following events may
occur: incoming signal instantly moves the positive customer from the system
is not empty, when it receives a signal, the following events may
occur: incoming signal instantly moves the positive customer from the system ![]() into the system
into the system
![]() with probability
with probability ![]() in this case, signal is referred
to as a trigger; or with
probability
in this case, signal is referred
to as a trigger; or with
probability ![]() signal is triggered by a
negative customer and destroys in QS
signal is triggered by a
negative customer and destroys in QS ![]() positive customer. The state
of the network meaning the vector
positive customer. The state
of the network meaning the vector ![]() where
where ![]() - the number of customers
at the moment
of time
- the number of customers
at the moment
of time ![]() at the system
at the system ![]() ,
, ![]() .
.
2. Description of incomes from the transitions between the states of the network
Let ![]() -
time of customers service in the system
-
time of customers service in the system ![]() with
the distribution function (DF)
with
the distribution function (DF) ![]() ,
, ![]() . Consider the dynamics of income
changes of
a network system
. Consider the dynamics of income
changes of
a network system ![]() ,
, ![]() . Let at the initial moment of time the income of
this QS be equal to
. Let at the initial moment of time the income of
this QS be equal to ![]() . We are interested
in income
. We are interested
in income ![]() at time t. The income of its QS
at moment time
at time t. The income of its QS
at moment time ![]() can be represented in the
form
can be represented in the
form ![]() , where
, where ![]() -
income changes of the system
-
income changes of the system ![]() at the time interval
at the time interval
![]() ,
, ![]() .
.
To find the income of the system ![]() we write the conditional probabilities
of the events that may occur during
we write the conditional probabilities
of the events that may occur during ![]() . The following cases
are possible:
. The following cases
are possible:
1) with
probability ![]() to the system
to the system ![]() from the external environment
a positive customer will arrive, which will bring an income in the amount of
from the external environment
a positive customer will arrive, which will bring an income in the amount of ![]() , where
, where ![]() - RV with expectation (E) of
which equals
- RV with expectation (E) of
which equals ![]() ,
, ![]() ;
;
2) with probability ![]() in the QS
in the QS ![]() from the external environment
a signal will arrive, which will bring an income (loss) in the amount of signal
is triggered by a negative customer and destroys in QS
from the external environment
a signal will arrive, which will bring an income (loss) in the amount of signal
is triggered by a negative customer and destroys in QS ![]() positive customer, which will bring a
loss in the amount of
positive customer, which will bring a
loss in the amount of ![]() ,
where
,
where ![]() - RV with E
- RV with E ![]() ,
, ![]() ;
;
3) the incoming
signal instantly moves the positive customer from the system ![]() into the system
into the system ![]() probability
of this event equals
probability
of this event equals ![]()
![]() ,
, ![]() by this transition the income of
by this transition the income of ![]() is reduced by the amount
is reduced by the amount ![]() , and income of
, and income of ![]() is
increased by this amount, where,
is
increased by this amount, where, ![]() - RV with E
- RV with E ![]() ,
, ![]() ;
;
4) with probability ![]() a positive customer will depart from
the network to the external environment, while the total amount of income of QS
a positive customer will depart from
the network to the external environment, while the total amount of income of QS
![]() is reduced by an amount which is equal
to
is reduced by an amount which is equal
to ![]() , where
, where ![]() - RV with E
- RV with E
![]() ,
, ![]() ;
;
5) with probability ![]() a customer from the
system
a customer from the
system ![]() transit to the system
transit to the system ![]() as a signal, if in it there were no
customers, and the income of
as a signal, if in it there were no
customers, and the income of ![]() is reduced by the
amount
is reduced by the
amount ![]() , where
, where ![]() - RV with E
- RV with E
![]() ,
, ![]() ;
;
6) a customer from
the QS ![]() transit to the system
transit to the system ![]() with probability
with probability ![]()
![]() ,
, ![]() by such a transition the income of
system
by such a transition the income of
system ![]() is reduced by the amount
is reduced by the amount ![]() and the income of system
and the income of system ![]() is
increased by this amount,
is
increased by this amount, ![]()
![]() ,
, ![]() ,
, ![]()
7) with probability ![]() positive customer transit from the
system
positive customer transit from the
system ![]() to the system
to the system ![]() , wherein the income of the QS
, wherein the income of the QS ![]() will increase
by the value of
will increase
by the value of ![]() , and the income of
, and the income of ![]() is reduced by this amount,
is reduced by this amount, ![]() ,
, ![]() ,
, ![]()
8) after
finishing servicing of a positive customer in QS ![]() it
is sent to
it
is sent to ![]() as
a signal, which is triggered by a negative customer and destroyed in QS
as
a signal, which is triggered by a negative customer and destroyed in QS ![]() positive customer; the probability of
this event equals
positive customer; the probability of
this event equals ![]() ; wherein the income of the QS
; wherein the income of the QS
![]() will reduce by value
will reduce by value ![]() , and the income of
, and the income of ![]() is reduced also by the amount,
is reduced also by the amount, ![]() ,
, ![]() ,
, ![]()
9) after finishing
servicing of positive customer in QS ![]() , it is sent to
, it is sent to ![]() as
a signal, which instantly moves the
positive customer from the system
as
a signal, which instantly moves the
positive customer from the system ![]() into the system
into the system ![]() the probability of this
event equals
the probability of this
event equals ![]() ,
, ![]() ,
, ![]() ,
, ![]() by such a
transition the income of system
by such a
transition the income of system ![]() and
and ![]() reduced
by the amount
reduced
by the amount ![]() , and income of system
, and income of system ![]() is increased by
this amount respectively, where
is increased by
this amount respectively, where ![]() - RV with
the E
- RV with
the E ![]() ,
, ![]() ,
, ![]()
![]()
10) with probability ![]() on time interval
on time interval ![]() network state will not change;
network state will not change;
11) for every small time interval ![]() system
system
![]() because of customers’ presence
in it increases its income by the amount of
because of customers’ presence
in it increases its income by the amount of ![]() ,
where
,
where ![]() - RV with the E
- RV with the E ![]() ,
, ![]() .
.
3. Finding the expected incomes of the network systems
Income changes of the QS ![]() on interval
on interval ![]() can
be written as:
can
be written as:
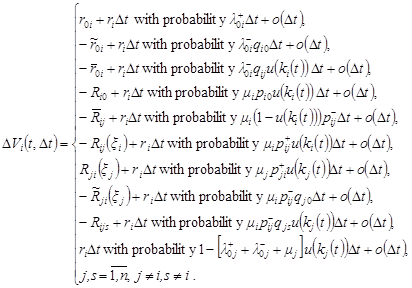 | (1) |
Let us find the expression for the expected
income of the system ![]() in time
in time ![]() suppose, all the network systems
operate under heavy-traffic regime, i.e.
suppose, all the network systems
operate under heavy-traffic regime, i.e. ![]()
![]()
![]() Taking into account (1) for the E
or income changes we can write:
Taking into account (1) for the E
or income changes we can write:
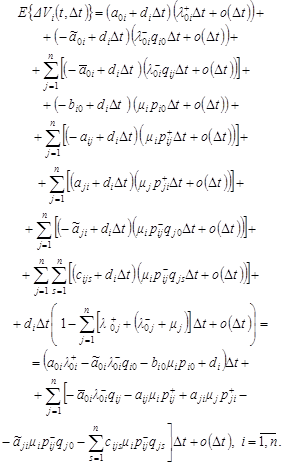 |
Then, similarly as in [3], we obtain
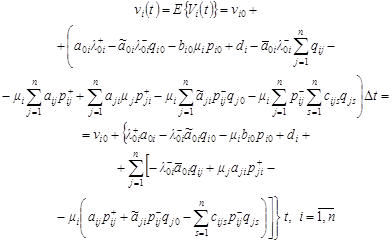 | (2) |
4. Finding variances of the incomes of the network systems
As in
[4], system income ![]() can be presented in form
can be presented in form ![]() , where
, where ![]() - count of partitions of the interval
- count of partitions of the interval ![]() by equal parts,
by equal parts, ![]() ;
;
![]() - income changes i-th
QS on l-th time interval,
- income changes i-th
QS on l-th time interval, ![]() ,
, ![]() . To calculate the variance of the
system income in the network, we introduce the following designations:
. To calculate the variance of the
system income in the network, we introduce the following designations:
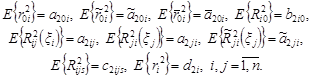 |
Let us consider the square of the difference ![]()
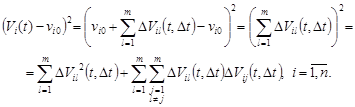 | (3) |
Let us find the expectations of summands in
the right side of the last equality. For
this we write support equalities considering that RV and functions of RV
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() pairwise independent from
pairwise independent from ![]() ,
, ![]() . Then
. Then
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Considering (4)-(11), we have:
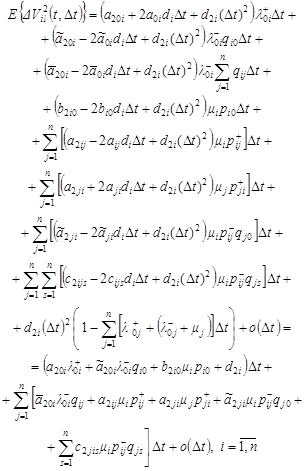 | (12) |
Insofar
as the values ![]() and
and ![]() are independent at
are independent at ![]() using (12)
one can find
using (12)
one can find
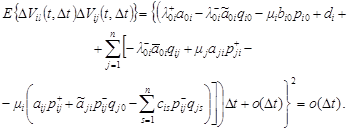 | (13) |
Then, further, passing to the limit ![]() from (3),
(12), (13) and also, that
from (3),
(12), (13) and also, that ![]() obtain
obtain
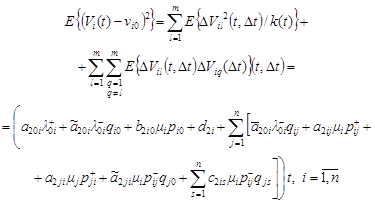 | (14) |
Now let us find an expression for ![]() , using (2):
, using (2):
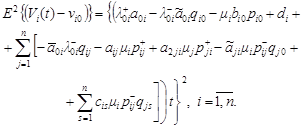 | (15) |
In this way, the variance of income of i-th QS, considering (14), (15), can be written in the form
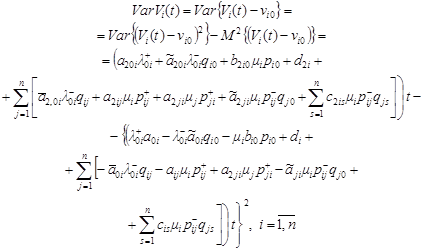 | (16) |
5. Numerical example
As is
known (see [5]), relation for the expected income of the system ![]() in the case,
where there are no negative customers in the network and all systems operate in
a heavy-traffic regime, has the form:
in the case,
where there are no negative customers in the network and all systems operate in
a heavy-traffic regime, has the form:
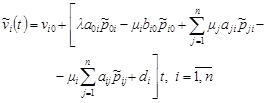 | (17) |
where: ![]() - input rate
of customers;
- input rate
of customers; ![]() - probability of a
customer arriving to the system
- probability of a
customer arriving to the system ![]() ,
, ![]() ,
, ![]() ;
; ![]() - probability that the customer
which finished servicing in i-th QS move to j-th QS,
- probability that the customer
which finished servicing in i-th QS move to j-th QS, ![]() ,
, ![]() ;
; ![]() - probability of the
departure of a customer,
- probability of the
departure of a customer, ![]()
![]() . Relation for the expected income of
the system
. Relation for the expected income of
the system ![]() with negative customers but without
considering input signals, can be written as [6]:
with negative customers but without
considering input signals, can be written as [6]:
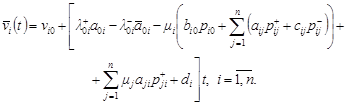 | (18) |
Let n = 10; input rates of
positive customers and signals ![]() and
and ![]() respectively equal
respectively equal ![]() ,
, ![]() ,
, ![]() . Service rates of customers
. Service rates of customers ![]() equal
equal ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Let
us transition probabilities of positive customers
. Let
us transition probabilities of positive customers ![]() respectively
equal:
respectively
equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , other equal zero. Probabilities, that
were serviced in
, other equal zero. Probabilities, that
were serviced in ![]() , move to
, move to ![]() as
negative, equal:
as
negative, equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
other equal zero. Departure probabilities equal
,
other equal zero. Departure probabilities equal ![]() ,
, ![]() . Probabilities of a signal
arriving, which are instantly moves the positive customer from the system
. Probabilities of a signal
arriving, which are instantly moves the positive customer from the system ![]() to the system
to the system ![]() respectively equal:
respectively equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
other equal zero. Probabilities that signal is triggered as a negative customer
and destroys
in QS positive customer equal:
,
other equal zero. Probabilities that signal is triggered as a negative customer
and destroys
in QS positive customer equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Let us set values for the required
expectations: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
other equal zero.
,
other equal zero.
Expectations
for the random system of incomes has been calculated. Their values have the form: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Let us suppose that income at the initial time equals ![]()
![]() .
Consider the length of the time interval of 10 hours,
.
Consider the length of the time interval of 10 hours, ![]() ,
,
![]() . Then using formulas (2), (17), (18)
analytical expressions have been found for the expected system
incomes of the networks.
. Then using formulas (2), (17), (18)
analytical expressions have been found for the expected system
incomes of the networks.
In Figure 1, income changes is shown of the QS ![]() for HM-network with
negative customers and without them, and also with
signals. One can see that
the negative customers reduce
expected income of the system
for HM-network with
negative customers and without them, and also with
signals. One can see that
the negative customers reduce
expected income of the system ![]() Signals inputting also influence the income changes, reducing it.
Signals inputting also influence the income changes, reducing it.
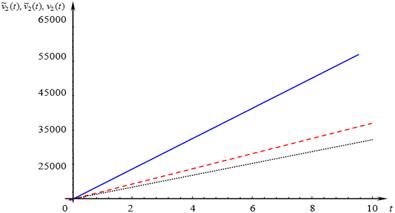
Fig. 1. Income changes of the S2 QS, solid line - a case without negative customers, dashed - a case with negative customers, dotted - taking into account the signals
6. Conclusions
In this paper a method was proposed for finding expected incomes in HM-network systems with positive and negative customers and also with signals. Incomes from the transitions between the states of the network are RV with given mean values. This method is based on the using of found approximate and exact expressions for the mean values of the random incomes. An example was calculated. The expres- sions for the variances of incomes of QS was obtained. The obtained results can be used in modeling income changes in various CSN, the virus penetration into it, and also to load control in CSN.
References
[1] Gelenbe E., G-networks with triggered customer movement, Journal of Applied Probability 1993, 30, 742-748.
[2] Matalytski M., Naumenko V., Investigation of G-network with signals at transient behavior, Journal of Applied Mathematics and Computational Mechanics 2014, 13(1), 75-86.
[3] Naumenko V., Matalytski M., Finding the expected incomes in the Markov G-network with signals, Vestnik of GrSU. A Series of Mathematics, Physics, Computer Science, Computer Facilities and Management 2014, 2, 134-143.
[4] Naumenko V., Matalytski M., Investigation and application of G-networks with incomes and signals with random time activation Vestnik of GrSU. A Series of Mathematics, Physics, Computer Science, Computer Facilities and Management 2014, 3, 142-152.
[5] Matalytski M., On some results in analysis and optimization of Markov networks with incomes and their application, Automation and Remote Control 2009, 70(10), 1683-1697.
[6] Naumenko V., Matalytski M., Analysis of Markov net with incomes, positive and negative customers, Informatics 2014, 1, 5-14.


