Recurrence relations for two-channel queueing systems with Erlangian service times and hysteretic strategy of random dropping of customers
Yuriy Zhernovyi
,Bohdan Kopytko
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
RECURRENCE RELATIONS FOR TWO-CHANNEL QUEUEING SYSTEMS WITH ERLANGIAN SERVICE TIMES AND HYSTERETIC STRATEGY OF RANDOM DROPPING OF CUSTOMERS
Yuriy Zhernovyi 1, Bohdan Kopytko 2
1 Ivan
Franko National University of Lviv, Lviv, Ukraine
2 Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
yu.zhernovyi@lnu.edu.ua, bohdan.kopytko@im.pcz.pl
Received: 2 May 2018; Accepted: 18 June 2018
Abstract. This article proposes a method of study the M/Es/2/m and M/Es/2/∞ queueing systems with a hysteretic strategy of random dropping of customers. Recurrence relations are obtained to compute the stationary distribution of the number of customers and steady-state characteristics. The constructed algorithms were tested on examples with the use of simulation models constructed with the help of GPSS World.
MSC 2010: 60G10, 60J28, 60K25, 93B40
Keywords: two-channel queueing system, Erlangian service times, random dropping of customers, fictitious phase method, hysteretic strategy, recurrence relations, steady-state characteristics
1. Introduction
For investigating queueing systems with
Erlang distributions and, in particular, the M/Es/n/∞ system,
the fictitious phase method developed by A.K. Erlang [1]
is used. For the Erlang distribution of the sth order of service time,
it is supposed that each customer sequentially passes through ![]() phases of service whose
durations are distributed by exponential
laws with parameters
phases of service whose
durations are distributed by exponential
laws with parameters ![]() respectively.
respectively.
Accounting for phases requires the fixation of the corresponding states and leads to the increase in the cumbersomeness of the description of a queuing system with phase-type distributions. The direct solution of a system of equations for steady-state probabilities of states can result in being impossible in view of a large size of the coefficient matrix of a system. The algorithmic approach is most expedient since it presumes the obtaining of a solution to systems of equations in the form of recursive formulas or in the form of matrix recurrence relations and algorithms [2-10]. The method proposed in [7-10] is based on the use of direct recurrence relations following immediately from system equations for steady-state probabilities. It does not contain iterations and it does not presume preliminary transformations of the system of equations being solved.
The objective of this article is the
construction of recurrent algorithms with the help of the fictitious phase
method to compute the steady-state distribution of the number of customers in the M/Es/2/m
and M/Es/2/∞ queuing system, where ![]() with hysteretic strategy of the random
dropping of customers. The random dropping of customers is used in queuing
systems with a view for preventing overloads when each arriving customer can be
discarded with a definite probability dependent on the queue length at the
moment of arrival of a customer even if the buffer
is not completely filled [11-13].
with hysteretic strategy of the random
dropping of customers. The random dropping of customers is used in queuing
systems with a view for preventing overloads when each arriving customer can be
discarded with a definite probability dependent on the queue length at the
moment of arrival of a customer even if the buffer
is not completely filled [11-13].
2. The M/Es/2/m system with hysteretic strategy of random dropping of customers
Let us consider the M/Es/2/m system, where ![]() and
and
![]() is the maximum number of customers who
can simultaneously be in the queue. The input flow
of customers is Poisson, i.e., the time intervals between the moments of
arrival
of customers adjacent in time are independent random variables exponentially
distributed with the parameter
is the maximum number of customers who
can simultaneously be in the queue. The input flow
of customers is Poisson, i.e., the time intervals between the moments of
arrival
of customers adjacent in time are independent random variables exponentially
distributed with the parameter ![]() The service time of
each customer is distributed according to the generalized Erlang law, of the
order
The service time of
each customer is distributed according to the generalized Erlang law, of the
order ![]() so the service time is the sum of
so the service time is the sum of ![]() independent random variables
exponentially distributed with parameters
independent random variables
exponentially distributed with parameters ![]() respectively.
respectively.
We consider the random dropping of customers
that is implemented according to the following rule: if, at the moment of
arrival of a customer, the number
of customers in the system is equal to ![]() (without
making allowance for the arrived one),
then the customer is accepted for service with probability
(without
making allowance for the arrived one),
then the customer is accepted for service with probability ![]()
![]() and is refused
(discarded) with probability
and is refused
(discarded) with probability ![]()
We consider a hysteretic strategy of the
random dropping of customers with two thresholds ![]() and
and ![]() (
(![]() ) and with two operating modes, namely,
basic and dropping mode. Assume that
) and with two operating modes, namely,
basic and dropping mode. Assume that ![]() when
when ![]() for the basic mode and
for the basic mode and ![]() when
when ![]() for the dropping mode. The dropping mode
continues from the moment when the number of customers in the system achieves the value of
for the dropping mode. The dropping mode
continues from the moment when the number of customers in the system achieves the value of ![]() up to the moment when the number of customers is re-
duced to the value of
up to the moment when the number of customers is re-
duced to the value of ![]() If, at the moment of arrival of
a customer, the condition
If, at the moment of arrival of
a customer, the condition ![]() is satisfied, then the mode is not
changed. The rate of the simplest flow of customers accepted for service in the dropping mode is equal to
is satisfied, then the mode is not
changed. The rate of the simplest flow of customers accepted for service in the dropping mode is equal to ![]() In a partial case of the hysteretic
strategy, assuming that
In a partial case of the hysteretic
strategy, assuming that ![]() for all
for all ![]() in the dropping mode. If
in the dropping mode. If ![]() then
then ![]() where
where ![]()
The M/Es/2/m
system with the hysteretic strategy of the random dropping of customers we
denote by M(h1,h2)/Es/2/m.
We introduce the following designations for system states in the basic mode: ![]() signifies that customers are absent in the system;
signifies that customers are absent in the system; ![]() signifies that k customers are present in the system
signifies that k customers are present in the system ![]() and that two customers are at
the ith phase of
service and at the jth one
and that two customers are at
the ith phase of
service and at the jth one ![]() respectively. The states
respectively. The states ![]() correspond to one working channel and jth phase of
service. We
denote the steady-state probabilities of staying the system at the states
correspond to one working channel and jth phase of
service. We
denote the steady-state probabilities of staying the system at the states ![]() and
and ![]() by
by ![]() and
and ![]() respectively.
Let
respectively.
Let ![]() be the state similar to
be the state similar to ![]() in the dropping mode and
in the dropping mode and ![]() be
the steady-
state probability of staying the system at the state
be
the steady-
state probability of staying the system at the state ![]()
![]()
![]() We assume that
We assume that ![]()
![]()
To determine steady-state probabilities, we obtain the system of homogeneous algebraic equations with normalization condition
| (1) |
Introducing the notation
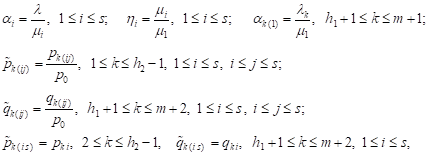 |
and using the system of algebraic equations, we find:
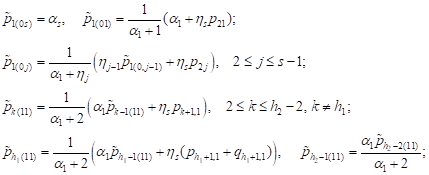 |
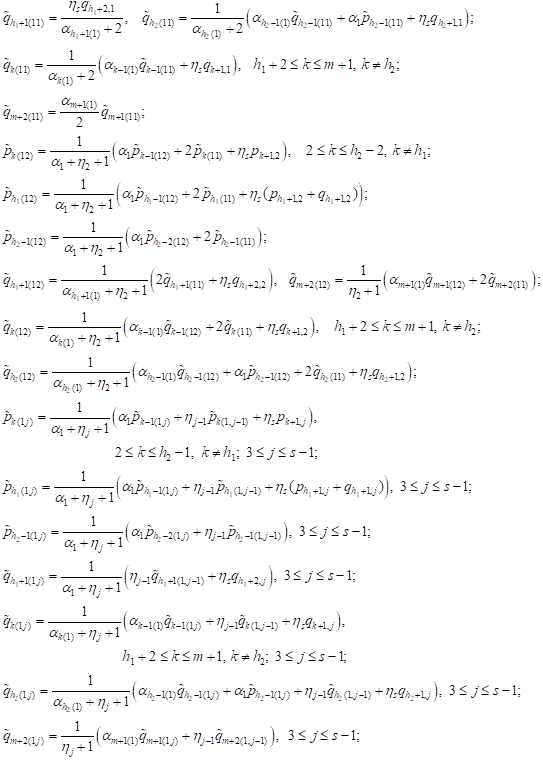
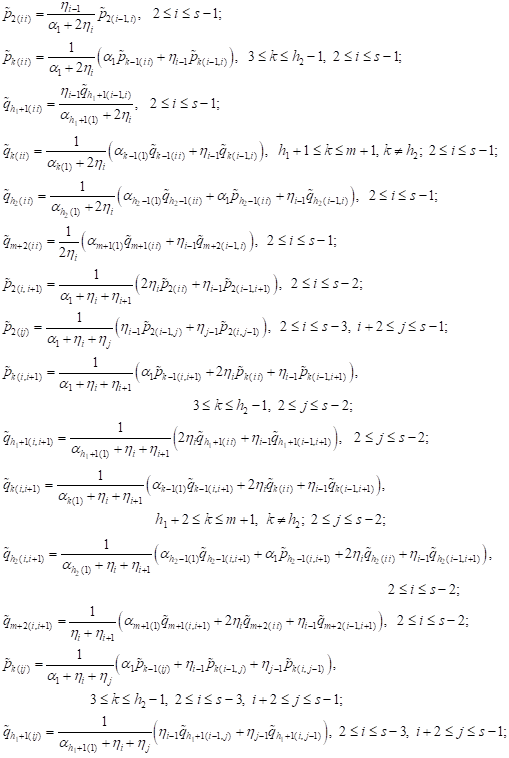
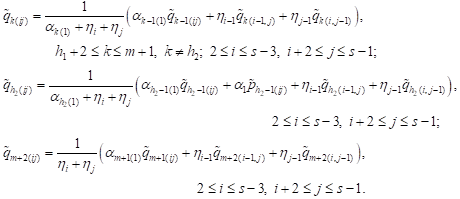 | (2) |
Recurrence
relations (2) allow one to compute ![]() and
and ![]() as linear func-
tions of the unknown parameters
as linear func-
tions of the unknown parameters ![]() and
and ![]()
![]() in
the following order:
in
the following order:

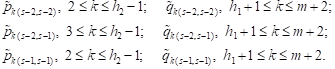 |
To
determine unknown parameters ![]() and
and ![]()
![]() we use the system that consists of
we use the system that consists of ![]() equations
that have not been involved in obtaining recurrence
relations (2),
equations
that have not been involved in obtaining recurrence
relations (2),
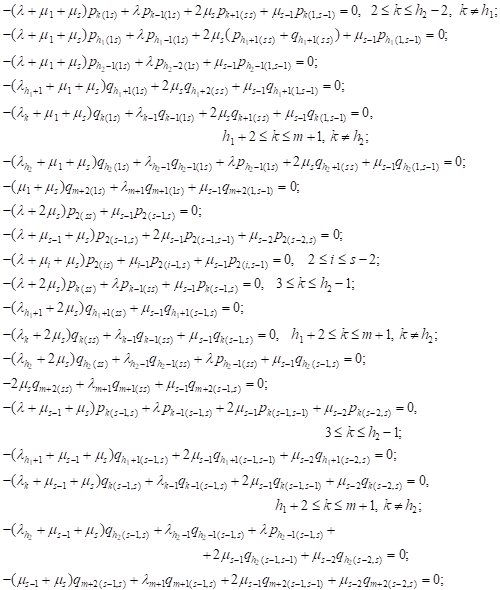
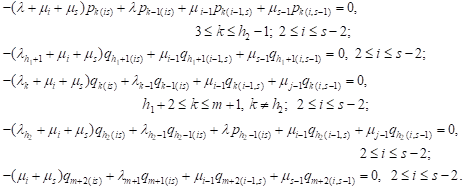 |
We use normalization condition (1) and determine the steady-state probabilities by the formulas
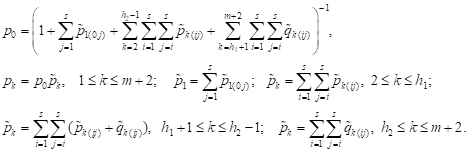 |
Here ![]() is steady-state
probability of presence
is steady-state
probability of presence ![]() customers in the
system.
customers in the
system.
We calculate the steady-state characteristics
- the average number of customers in
the system ![]() the average queue length
the average queue length ![]() average waiting time
average waiting time ![]() and service probability
and service probability ![]() - by the formulas
- by the formulas
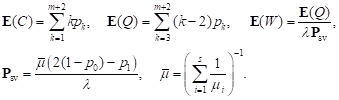 |
3. The system without restrictions on the queue length
For the M(h1,h2)/Es/2/∞
system, any constraint on the queue length is absent and, for the existence of
stationary distribution of the number of customers in the system, the condition ![]() must be satisfied. Determining approximate values of steady-state
probabilities
must be satisfied. Determining approximate values of steady-state
probabilities ![]() is reduced to the use of
recurrence relations (2) for large values of m.
We choose the number
is reduced to the use of
recurrence relations (2) for large values of m.
We choose the number ![]() so large that one of
the conditions (or each of these conditions) specifying the accuracy of
determining steady-state probabilities is
fulfilled. These conditions
can be specified, for example,
in the form
so large that one of
the conditions (or each of these conditions) specifying the accuracy of
determining steady-state probabilities is
fulfilled. These conditions
can be specified, for example,
in the form
| (3) |
Here ![]() and
and ![]() are positive numbers specifying the
required accuracy of computa-
tions;
are positive numbers specifying the
required accuracy of computa-
tions; ![]() and
and ![]() are approximate values of steady-state characteristics
are approximate values of steady-state characteristics ![]() and
and ![]() computed using steady-state probabilities
computed using steady-state probabilities ![]()
![]() is an approximate value of a
steady-state probability
is an approximate value of a
steady-state probability ![]() which is obtained
as a result of truncation of an infinite system of equations for
steady-state
probabilities.
which is obtained
as a result of truncation of an infinite system of equations for
steady-state
probabilities.
4. Numerical examples
Let us consider examples of determining
steady-state characteristics of
the M(h1,h2)/E5/2/∞
queuing system for different values of the thresholds ![]() and
and ![]()
![]() Let
Let ![]()
![]() the probabilities
the probabilities ![]() for the dropping
mode be set according to the rule:
for the dropping
mode be set according to the rule: ![]() for
for ![]() For comparison, we calculate the stationary character-
istics of the M/E5/2/43 system, which does not
apply the random dropping of
customers.
For comparison, we calculate the stationary character-
istics of the M/E5/2/43 system, which does not
apply the random dropping of
customers.
The
values of the steady-state probabilities ![]() and stationary characteristics of the M(h1,h2)/E5/2/∞ system
for cases 1-3, found using the recurrence relations
obtained in this paper, as well as of the M/E5/2/43 system, are presented in Tables 1 and 2. In order to
verify the obtained values, Table 2 contains the computing results
evaluated by the GPSS World simulation system [14] for the simulation time value
and stationary characteristics of the M(h1,h2)/E5/2/∞ system
for cases 1-3, found using the recurrence relations
obtained in this paper, as well as of the M/E5/2/43 system, are presented in Tables 1 and 2. In order to
verify the obtained values, Table 2 contains the computing results
evaluated by the GPSS World simulation system [14] for the simulation time value ![]()
In computing approximate values of steady-state
probabilities ![]() , the value of
, the value of ![]() was selected so large that conditions
(3) were satisfied when
was selected so large that conditions
(3) were satisfied when ![]() The obtained
minimal values of
The obtained
minimal values of ![]() for cases 1-3 are equal to 45, 45 and 47 respectively.
for cases 1-3 are equal to 45, 45 and 47 respectively.
Analyzing the results, presented in Table 2,
we see that the control of the input flow rate with the help of random dropping
of customers makes it possible to
considerably reduce the average queue length with an insignificant decrease in
the system throughput. Thus, the decrease in the average queue length in the M(h1,h2)/E5/2/∞ system (the case of ![]() ) in comparison with the M/E5/2/43 system amounts to 81.6%, with a decrease
in the relative throughput by 5.3%.
If the value of the threshold
) in comparison with the M/E5/2/43 system amounts to 81.6%, with a decrease
in the relative throughput by 5.3%.
If the value of the threshold ![]() increases, leaving the same value of
increases, leaving the same value of ![]() then
then ![]() and
and ![]() increase.
increase.
Table 1
Stationary distribution of the number of customers in the systems
|
|
Values of the
steady-state probabilities |
|||
|
M/E5/2/43 |
M(h1,h2)/E5/2/∞,
|
M(h1,h2)/E5/2/∞,
|
M(h1,h2)/E5/2/∞,
|
|
|
0 |
0.006270 |
0.030479 |
0.027564 |
0.025071 |
|
1 |
0.014577 |
0.070856 |
0.064078 |
0.058284 |
|
2 |
0.019569 |
0.095119 |
0.086020 |
0.078242 |
|
3 |
0.021658 |
0.105274 |
0.095203 |
0.086595 |
|
4 |
0.022351 |
0.108637 |
0.098247 |
0.089366 |
|
5 |
0.022544 |
0.109648 |
0.099131 |
0.090157 |
|
6 |
0.022589 |
0.107500 |
0.097400 |
0.088673 |
|
7 |
0.022597 |
0.101170 |
0.096390 |
0.088693 |
|
8 |
0.022598 |
0.080393 |
0.087893 |
0.083804 |
|
9 |
0.022598 |
0.058035 |
0.072205 |
0.075011 |
|
10 |
0.022598 |
0.040450 |
0.052594 |
0.063798 |
|
11 |
0.022598 |
0.028147 |
0.037520 |
0.050642 |
|
12 |
0.022598 |
0.019577 |
0.026111 |
0.036400 |
|
13 |
0.022598 |
0.013616 |
0.018162 |
0.025953 |
|
14 |
0.022598 |
0.009470 |
0.012632 |
0.018059 |
|
15 |
0.022598 |
0.006586 |
0.008785 |
0.012561 |
|
20 |
0.022598 |
0.001072 |
0.001430 |
0.002044 |
|
30 |
0.022598 |
0.000028 |
0.000038 |
0.000054 |
|
40 |
0.022598 |
7.517∙10-7 |
1.003·10-6 |
1.434·10-6 |
|
45 |
0.013559 |
8.236∙10-8 |
1.099·10-7 |
2.354·10-7 |
Table 2
Stationary characteristics of the systems
|
System |
Method |
Values of the stationary characteristics |
|||
|
|
|
|
|
||
|
M/E5/2/43 |
Recurrence |
22.88257 |
20.90968 |
21.19709 |
0.98644 |
|
GPSS World |
22.896 |
20.923 |
21.212 |
0.986 |
|
|
M(h1.h2)/E5/2/∞,
|
Recurrence |
5.71082 |
3.84263 |
4.11376 |
0.93409 |
|
GPSS World |
5.717 |
3.848 |
4.118 |
0.935 |
|
|
M(h1,h2)/E5/2/∞,
|
Recurrence |
6.18609 |
4.30530 |
4.57817 |
0.94040 |
|
GPSS World |
6.179 |
4.299 |
4.571 |
0.941 |
|
|
M(h1,h2)/E5/2/∞,
|
Recurrence |
6.71627 |
4.82469 |
5.10125 |
0.94579 |
|
GPSS World |
6.712 |
4.821 |
5.097 |
0.946 |
|
5. Conclusions
Using the method of fictitious phases, an
algorithm for calculating the stationary distribution of the number of
customers in the M/Es/2/m
systems with hysteretic strategy of the random dropping
of customers, inclusive of the case ![]() is constructed. The obtained recurrence
relations are used for the direct computation of the
solutions of the algebraic system for the steady-state
probabilities, which makes it possible to reduce the
amount of computations in comparison with the direct
or iterative classical methods. Using the obtained recurrence relations makes
it
possible to
reduce the number of solved equations from
is constructed. The obtained recurrence
relations are used for the direct computation of the
solutions of the algebraic system for the steady-state
probabilities, which makes it possible to reduce the
amount of computations in comparison with the direct
or iterative classical methods. Using the obtained recurrence relations makes
it
possible to
reduce the number of solved equations from ![]() to
to ![]()
References
[1] Brockmeyer, E., Halstrøm, H.L., & Jensen, A. (1948). The Life and Works of A.K. Erlang. Copenhagen: Danish Academy of Technical Sciences.
[2] Neuts, M.F. (1981). Matrix-geometric Solutions in Stochastic Models. Baltimore: The John’s Hopkins University Press.
[3] Bocharov, P.P., & Litvin, V.G. (1986). Methods of analysis and calculation of queuing systems with distributions of phase type, Avtomatika i Telemekhanika, 5, 5-23 (in Russian).
[4] Takahashi, Y., & Takami, Y. (1976). A numerical method for the steady-state probabilities of a GI/G/c queueing system in a general class. J. Oper. Res. Soc. Japan, 19, 2, 147-157.
[5] Ryzhikov, Yu.I. (1985). Recurrent calculation of multi-channel queueing systems with unlimited queue. Avtomatika i Telemekhanika, 6, 88-93 (in Russian).
[6] Ryzhikov, Yu.I. (1980). Algorithm for calculating a multichannel system with Erlang service. Avtomatika i Telemekhanika, 5, 30-37 (in Russian).
[7] Zhernovyi, K.Yu. (2017). Determining stationary characteristics of two-channel queueing systems with Erlangian distribution of service time. Cybernetics and Systems Analysis, 53, 1, 92-104.
[8] Zhernovyi, Yu.V., & Zhernovyi K.Yu. (2017). Determination of steady-state characteristics of three-channel queuing systems with Erlangian service times. Cybernetics and Systems Analysis, 53, 2, 280-292.
[9] Zhernovyi, Yu.V. (2017). Determining steady-state characteristics of some queuing systems with Erlangian distributions. Cybernetics and Systems Analysis, 53, 5, 776-784.
[10] Kopytko, B., & Zhernovyi, K. (2016). Steady-state characteristics of three-channel queueing systems with Erlangian service times. JAMCM, 15(3), 75-87.
[11] Chydziński, A. (2013). Nowe modele kolejkowe dla węzłów sieci pakietowych. Gliwice: Pracownia Komputerowa Jacka Skalmierskiego.
[12] Tikhonenko, O., & Kempa, W.M. (2013). Queue-size distribution in M/G/1-type system with bounded capacity and packet dropping. Communications in Computer and Information Science, 356, 177-186.
[13] Zhernovyi, Yu., Kopytko, B., & Zhernovyi K. (2014). On characteristics of the Mθ/G/1/m and Mθ/G/1 queues with queue-size based packet dropping. JAMCM, 13, 4, 163-175.
[14] Zhernovyi, Yu. (2015). Creating Models of Queueing Systems Using GPSS World. Saarbrücken: LAP Lambert Academic Publishing.

