Application of HM-networks with unreliable systems for finding the memory capacity in the information systems



APPLICATION OF HM-NETWORKS WITH UNRELIABLE SYSTEMS FOR FINDING THE MEMORY CAPACITY IN THE INFORMATION SYSTEMS

Mikhail Matalytski ¹, Pawel Zajac ², Dmitry Kopats ³

^1,2 Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
³ Faculty of Mathematics and Computer Science, Grodno State University
Grodno, Belarus
m.matalytski@gmail.com, pawel_zajac@vp.pl, dk80395@mail.ru

Received: 13 November 2017; Accepted: 22 May 2018

Abstract. To solve the problem of determining the memory capacity of the information systems (IS), it was proposed to use a stochastic model, based on the use of HM (Howard- -Matalytski) - queueing networks with incomes. This model takes into account the servicing of requests along with their volumes, the ability to change the volumes of the requests over time and the possibility of damaging IS nodes and their repairs, so servicing of demands can be interrupted randomly. The expressions are generated for the mean (expected) values of total requests volumes in the IS nodes.

MSC 2010: 60K20, 60K25, 68M20, 90B22

Keywords: HM-network, information systems, unreliable service, volumes of requests

1. Introduction

In IS, the total volume of memory is limited to a certain value, which is usually called memory capacity [1]. When designing systems, the main task is to find the expected volume of memory to take into account the conditions that limit the share of lost information. One of the methods for solving problems of IS design is the use of HM-queueing networks (QN) [2]. According to IS, we will continue to understand systems as information transformation objects, delivered in the form of messages (requests) [1]. HM-networks can be used to determine the volume of a buffer storage of systems that are representing processing IS nodes and transferring demands. Note that this problem is crucial, for example in the design of hubs or communication centers in information networks. The following model can also be used to solve an important problem that recently appeared in the IS, i.e., the problem of excessive buffering (the problem of determining the required memory volume) [3]. Bufferbloat - a phenomenon that occurs in packet communication networks, when the buffering causes an excessive increase in the time of the packets and packet delay variation, and the resulting decrease in the throughput volume of IS.

Neglect time dependence of requests processing of their volumes can lead to serious errors in finding the buffer memory in IS. The solution in the general case of the above problems can be based on the use of HM-networks with incomes. In such networks, the request during the transition from one queueing system (QS) to another brings some income last (which is equal to the volume of this request), and the income (volume) of the first QS is reduced by this amount.

Note that the method of finding non-stationary probabilities of states and finding average network characteristics with systems of medium unreliable network systems, operating under high load with the help of multidimensional generating functions are described in the monograph [4], the HM-network with unreliable service [4, 5]. For the first time, the use of HM-networks to estimate the volume in IS has been described in [6]. In [7, 8], a proposed method of finding the expected volume of homogeneous requests in open network systems with limited waiting times in queues systems, and in [9] - in the HM-network with limited sojourn times of requests.

2. Finding the expected volumes of requests in the case, when is known only first moments other incomes the transitions between the network states

Let’s look at QN with unreliable QS. Suppose S₀ handles are reliable, and in other systems S₁,...,S_n lines can be damaged. The state of the system S_i is described by the vector , where are the number of requests and undamaged lines in the system S_i at time t, respectively, Next, let’s specify the vector as the state of the network. Assume that the servicing times, the line operating times, and line repair times are independent random variables (RV). The servicing time for IS requests has an exponential distribution with a parameter ; the operation time of each line without damage in this system has an exponential distribution with the parameter After the damage of the line immediately begins repairing it, the repair time also has an exponential distribution with the parameter . Assume that if the line receives a damage while servicing the call, the request servicing will continue after the line has been repaired. We assume that the discipline of servicing requests in all systems is FIFO. Then at the time interval , the request can be handled on every line of the system S_i with the probability , the line with the probability may be damaged or corrected with the probability Let us denote by p_ij - the probability of passing the request after serving in the S_i system to the S_j system, matrix is a matrix of transition probabilities of the irreducible Markov chain.

Let’s look at the dynamics of the change in the expected volume of requests in some S_i network systems. Let be the volume at time t, and at the beginning of time the system has the volume Then this volume at the given QS at time Δt can be expressed by the formula

,

(1)

where - a change in the volume of requests in the system S_i in the time interval . To find this value, you need to find the probabilities of events that may occur at time and volume changes in the S_i system associated with these events.

1. With probability

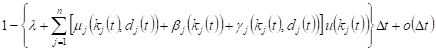in the time interval the change in system state S_i will not take place, the volume of requests in that system increases by , where , .

2. With probability a request after servicing in S_i , goes to the external environment, the volume of requests in system S_i decreases by the value of , where , .

3. With probability , a request from the outside environment enters the system S_i and increases the volume of requests to the size , , .

4. With probability a request, after servicing in the S_i system, goes to the system S_j ; the volume of requests in system S_i changes by the value , where , , .

5. With probability a request, after servicing in system S_j goes to the system S_i ; the total volume of requests in the system S_i will increase by the value of , where , , .

6. With probability a number of active lines in system S_j decreases by 1, the volume of requests in the system S_i will increase by the value , .

The following cases are possible.

7. The number of operating lines in the system S_j will decrease by 1, the request after servicing in the system S_i will go to the external environment, .

8. The service line in the system S_j is damaged, the request enters the system S_i from the outside environment, .

9. The number of service lines in the system S_s will be reduced by 1, the request after servicing in the system S_i will go to the system S_j, , .

10. The number of service lines in the system S_s will decrease by 1, the request after servicing in the system S_j will go to S_i, , .

The probabilities of the corresponding events in cases 7-10 are equal , for example, in case 7 for this probability we have

.

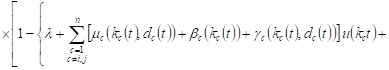
Changes in the volume of expected requests in the system S_i :

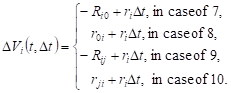11. With probability , a number of service lines in system S_j will increase by 1, and the total volume of requests in the system S_i by , , .

12. With probability one line of service is being repaired in the system S_i , the total volume of applications will decrease by , where , - RV with distribution function - repair fee for the service line in the system S_i ,.

In addition, the following cases are possible.

13. There will be a repair of the service line in the system, the request after servicing in the system S_j will go to the external environment; , .

14. The service line will be repaired in the system S_i , system S_i will go to the outside environment; .

15. The service line will be repaired in the system S_j , the system enters a request from the outside environment; .

16. There will be repair of the service line in the system S_i , and in this system is entering a request from the outside environment, .

17. There will be repair of the service line in the system S_s , the request after servicing in the system S_i will go to system S_j , , , .

18. The system S_i will repair the service line, the request after the servicing system goes to S_j , , .

19. There will be repair of the service line in the system S_s , the request after servicing system S_j goes to S_i , , , .

20. There will be repair of the service line in the system S_i , the request after the servicing system S_j goes to S_i , , .

21. The system S_c will repair the service line, the system will be damaged and the status of the other QS will not change,, .

22. The service line will be repaired in the system S_i , the service line will be damaged in the system S_s and will not change states of other QS, .

The probabilities of events taking place in 13-22 cases will be equal , because, for example, in case 13 we will have

.

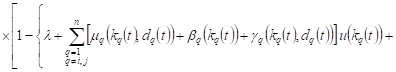
Changes in the expected volume of requests in the system S_i in cases 13-22 are as follows:

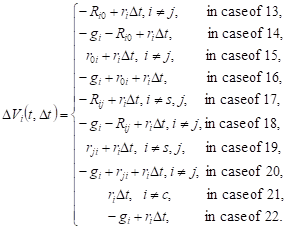The following cases are possible:

23. The service line will be repaired in the system S_c , the service line will be damaged in the system S_s , will not change states of other QS, and after the operation in the system will go to the outside environment, , .

24. The service line will be repaired in the system S_i , the service line will be damaged in the system S_s , the request after servicing system goes to the outside environment, .

25. The service line will be repaired in the system S_c , the service line will be damaged in the system S_s , the request goes into the system from the outside environment, , .

26. The service line will be repaired in the system S_i , the service line will be damaged in the system S_s , the request goes into the S_i system from the outside environments, .

27. The service line will be repaired in the system S_c , the service line will be damaged in the system S_s , the request after servicing in system S_i goes into the S_j , , , .

28. The service line will be repaired in the system S_i , the service line will be damaged in the system S_s , the request after servicing in system S_s goes into the S_j , , .

29. The service line will be repaired in the system S_c , the service line will be damaged in the system S_s , the request after servicing in system S_j goes into the S_i , , , .

30. The service line will be repaired in the system S_i and the service line will be damaged in the system S_s . The request after servicing in system goes into the S_i , , .

In appropriate cases, the probability of 23-30 events are equal For example, in case 23, the probability will be equal

.

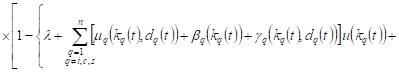
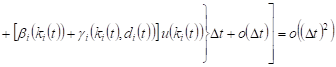We will assume that RV , , , , , are independent, , . The changes of the volumes of requests in the system S_i in cases 23-30 are equal to:

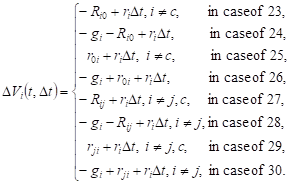With constant execution of the process with can be written

, .

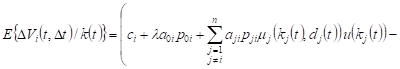
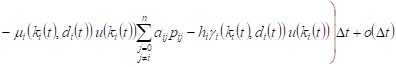Averaging after , taking into account the condition of normalization , we will obtain the change in the expected volume of the system S_i

, .

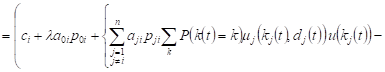
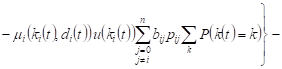
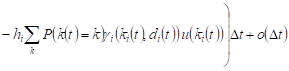Let the system S_i at the time t have , . In each of them, the servicing time, the work time and the repair time of damaged lines have an exponential distribution with parameters, , and respectively, . Assume that the intensity of request servicing and the intensity of repair of damaged lines in the system S_i depends linearly on the number of requests and the number of damaged lines.

, .

We will also assume that the averaging of the expression of is , i.e. .

In addition, , where , respectively mean the number of requests (waiting and servicing) and the average number of lines operating in the system S_i at the time t, . Given these assumptions, we obtain the approximate

.

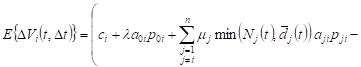
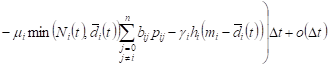(2)

Because the operating times and repair lines in the system S_i have an exponential distribution, - the average number of service lines repaired over time in the system S_i , - the average number of service lines in the system S_i damaged over time , . Therefore , , where , we get a linear differential equation , , and with the initial condition we have:

, .

(3)

The equation for the average number of requests in the QS network has the form

, .

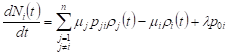(4)

It is moved in the same way as in [4] for networks with another feature. The average number of occupied service lines in the system S_i can be approximated by an expression . Then the system of equations (4) has the form

, ,

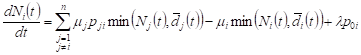(5)

This is a system of regular linear differential equations with discrete right sides, which can be solved by dividing the phase spaces into a number of areas and finding solutions in each of them.

From (1), (2) it follows

.

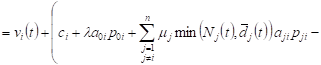
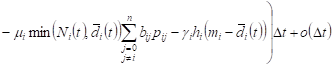When , we have heterogeneous first order linear equations

, .

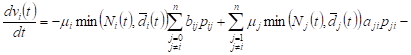
(6)

By setting up the initial conditions , , you can find the expected volume of network systems.

If the network is functioning in such a way that on average there are no queues in it, ie. , , the formulas (5) (6) will have the form:

, ,

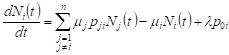(7)

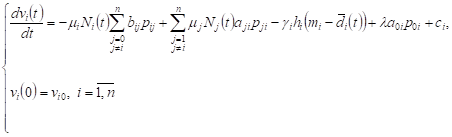(8)

3. Expected volumes of requests in central network system

Let’s consider a closed network with a central QS. Let peripheral networks do not have queues on average, ie , , and the central system operates in high load conditions, ie . The system (5) in this case can be rewritten as

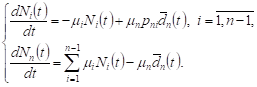(9)

The general solution of the system (9) having (3) at the initial conditions, , , is equal

, , ,

where , , , - number of requests in the network. For those , , the system (8) for the expected volume of requests in network systems takes the form

, , .

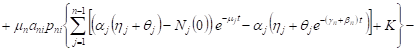
By integrating these systems with initial conditions, , , we have

, ,

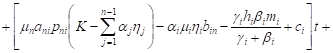
(10)

.

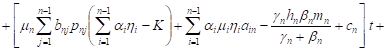
(11)

4. Conclusions

The article received approximate expressions for finding expected revenues in HM-network systems. These systems can be used when finding the expected memory space in information systems. Further research in this direction may be related to the analysis of arbitrary (non-Markov) random volume registrations and Markov chains applications with other peculiarities, such as limited queue time and faulty service systems.

References

[1] Tikhonenko, O. (2006). Metody personalistyczne analizy systemów informacyjnych. Akademicka Oficyna Wydawnicza EXIT.

[2] Matalytski, M., Tikhonenko, O., & Koluzaeva, E. (2011). Systems and queueing networks: analysis and application [In Russian: Sistemy i seti massovogo obsluzhivanija: analiz i primenenija]. GrSU.

[3] Bufferbloat [Electronic resource]: Wikipedia: http://en.wikipedia.org/wiki/Bufferbloat.

[4] Matalytski, M., & Statkevich, S. (2014). Stochastic network with bounded waiting time of claims and unrealiable service. [In Russian: Stohasticheskie seti s ogranichennym vremenem ozhidanija zajavok i nenadjozhnym obsluzhivaniem]. GrSU.

[5] Matalytski, M. (2015). Analysis and forecasting of expected incomes in Markov network with bounded waiting time for the claims. Automation and Remote Control, 76(6), 1005-1017.

[6] Matalytski, M., & Naumenko V. (2015). Zastosowanie HM-sieci kolejkowych dla wyznaczenia objętości pamięci systemów informacyjnych. Studia Informatica, 35(3), 63-69.

[7] Matalytski, M., & Zajac, P. (2016). Finding of expected volumes of request in systems of the queueing network with limited amount of spaces of expectations. Studia Informatica, 36(1), 89-104.

[8] Matalytski, M., & Zajac, P. (2017). Expected volumes of requests in systems of the queueing network with a limited number of waiting places. Scientific Issues Jan Długosz University in Częstochowa Mathematics XXII, 141-160.

[9] Matalytski M., & Zajac, P. (2017). Application of HM-networks with impatient claims in finding the memory capacity in the information systems. Journal of Applied Mathematics and Computational Mechanics, 16(3), 47-59.