Analysis of thermal cycles and phase transformations during multi-pass arc weld surfacing of steel casts taking into account heat of the weld
Jerzy Winczek
,Marek Gucwa
,Krzysztof Makles
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
ANALYSIS OF THERMAL CYCLES AND PHASE TRANSFORMATIONS DURING MULTI-PASS ARC WELD SURFACING OF STEEL CASTS TAKING INTO ACCOUNT HEAT OF THE WELD
Jerzy Winczek, Marek Gucwa, Krzysztof Makles
Institute of
Mechanical Technology, Czestochowa University of Technology
Czestochowa, Poland
winczek@imipkm.pcz.czest.pl, mgucwa@spaw.pcz.pl,
krzymakles@gmail.com
Received: 2 January 2018;
Accepted: 14 February 2018
Abstract. In this work, a model of phase transformations during multipass weld surfaced steel casts is presented. In the temperature field calculation algorithm, the influence of the heat of overlaying beads and a self-cooling of previously overlayed beads have been taken into account. The fusion area, full and part transformation zones, by solidus, A1 and A3 and A1 temperatures has been determined, respectively. The temperatures of the beginning and the end of the phase changes during cooling were determined on the basis of the time-temperature-transformation welding diagram. In the phase change kinetic description, the JMAK law and KM formula were used. Theoretical considerations are illustrated by example of volume share calculations of particular structural components during the weld surfaced 230-450 W steel cast. The results of computation in the graphical forms are presented: welding thermal cycle diagrams and structural share change histories at selected points, as well as temperature and the phase share distributions in cross section.
MSC 2010: 74F05, 74A50, 80A20
Keywords: surface treatment, temperature field, phase transformations, welding, surfacing
1. Introduction
Regeneration of machine parts that undergo intense wear during exploitation, especially within heavy working machines, are carried out mainly by welding technology. Modeling of thermo-mechanical states in the surfacing or rebuilding by welding requires the calculations of temperature field, the calculation of the structural shares as a result of phase transformations, as well as temporary and residual stresses. A repair or regeneration of castings is often performed by the use of welding techniques. In this scope, intense research on overlaying welding (rebuilding, hard surfacing) is carried out. In the modeling of these processes, the analysis of thermo-mechanical states of castings is also considered.
In most analytical and numerical solutions of the differential heat conduction equation, the single-distributed heat source model is adopted [1-12]. The use of such a heat source model does not allow one to get the irregular shape of the fusion line. There are few works completely modeling thermo-mechanical phenomena during multi-pass welding that take into account changeable temperature field phase transformations using FEM [13-19]. In a few works [20-23] only results of experimental investigation have been presented.
During multi-pass welding (rebuilding, hard surfacing), subsequent electrode transitions heat up previously made welds and also melt them. Multiple welding thermal cycles often cause several phase transformations, which result in structural differentiation of the material in the heat affected zone.
2. The model of temperature field
In the calculation of the temperature field, the bimodal heat source model has been applied. The heat density distribution of this source is the sum of the heat distributions caused by the following models: the heat source model of the melted electrode and the heat source model of heat induced by direct action of the electric arc. The total amount of heat generated in the process is the sum of heat transferred through the molten electrode and emitted by an electric arc, which can be recorded as follows:
| (1) |
where: ΔTa(x,y,z,t) - the temperature increase caused by heat emitted by an electric arc, ΔTw(x,y,z,t) - the temperature increase caused by the heat transferred through molten electrode to reinforcement.
Temperature field description caused by the Gaussian heat source model of the electric arc impact is shown in [24]. The heat source model of the melted electrode and the temperature field induced by action of this heat source are described in [25].
In the temperature field calculation during multi-pass weld surfacing, the heating up from previously made welds and cooling of previously heated areas have been taken into account. The temperature field of multi-pass overlaying welding (Fig. 1) during the overlaying of the k-th pad weld is expressed by the relationship:
| (2) |
where: DTjC - a increase in temperature caused by already previously overlayed j-th bead, DTjH - temperature increase during padding of the k-th bead.
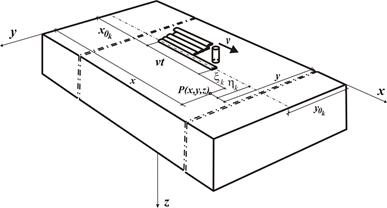
Fig. 1. The multi-pass overlaying welding scheme
Whereas after application of all beads, the relationship for the temperature calculation is as follows:
| (3) |
3. Kinetics of phase transformation in solid state
In quantification, the progress of phase transformations in steel during the thermal welding cycle is described by Johnson-Mehl-Avrami’s and Kolomogorov’s (JMAK) formula [26, 27] for diffusive transformation and Koistinen-Marburger (KM) rule for martensitic transformation [28]. During heating, the phase transformations of the initial structure into austenite occur after exceeding the critical temperature A1, and end at the temperature A3. The volume participation of austenite jA created during heating is calculated in relation to the temperature of the process in to the temperatures A1 and A3. The amount of created austenite is defined by the JMAK rule [26]:
| (4) |
where jj0 denotes initial volumetric share (j º F - ferrite, j º P - pearlite, j º B - bainite), jA0 denotes the amount of residual austenite remaining from the previous welding thermal cycle. The constant bj and nj are determined depending on the values A1 and A3:
| (5) |
| (6) |
In multi-pass welding, the volume shares of particular structures during cooling, the temperature, cooling rate, and the share of austenite (incomplete autenitization 0 £ jA £ 1) are dependent. To describe the kinetics of the transformation of austenite into ferrite, pearlite or bainite during cooling, the principle of additivity can be applied, and then the volume fraction of the newly formed phase jj is expressed by [27]:
| (7) |
where: jj0 - volume share of j-th structural constituent, which earlier has not been transformed into austenite, φjmax - the maximum volume fraction of phase j-th dependent on cooling rate, determined on the basis of the TTT - diagram (Fig. 2). The sum of structural constituent shares equals:
| (8) |
and k - the number of structural constituents.
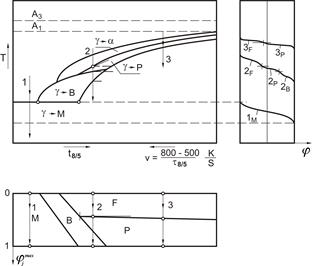
Fig. 2. Diagram of phase transformations of supercooled austenite depending on the cooling rate within temperature between 800-500°C
The quantitative description of material structure dependence on temperature and transformation time of supercooled austenite is made on the basis of a time-temperature-transformation welding diagram for continuous cooling (TTT - welding diagram). In this diagram, the progress of the phase transformation depends on the process temperature and the cooling time t8/5 (material time between 500°C and 800°C) or the cooling rate v8/5, which is the material cooling velocity between 500°C and 800°C (v8/5 = (800-500)/t8/5). The temperatures of the beginning and end of the austenite transformation into cooling structures, as well as the t8/5 can also be determined by means of analytical dependiences [29]. Replacing the time t in the equation (7) by the new variable - the temperature T [30], the equation for volume share of constituent will be written as follows:
| (9) |
where
| (10) |
| (11) |
jj - volume share of the created structural constituent, j º F - ferrite, j º P - pearlite, j º B - bainite), Tjs = Tjs(v8/5) and Tjf = Tjf(v8/5) - start and final temperature of the transformation of this constituent, respectively, jjmax - the maximal contribution of the structural constituent j, which will be created from the supercooled austenite for specified v8/5.
The volume share of martensite jM formed from austenite for process temperature T below Ms (initial temperature of martensitic transformation) is calculated using the Koistinen-Marburger rule [28]:
| (12) |
where
| (13) |
where: Mf - temperature of the end of martensitic
transformation, ![]() .
.
4. Tempearature field and phase share calculations
Numerical simulations of the temporary temperature field and phase changes are conducted for the prismatic 230-450 W steel cast of length 0.5 m, width 0.2 m, thickness 0.03 m.
In the simulation, 6 welds are applied in the middle part of a welded element (the coordinate of weld beginning x0 = 0.15 m) of length l = 0.5 m. The surfaced area on the top surface of the plate with a sequence of the weld padding is presented in Figure 3, where a horizontal dashed line denotes the location of a cross section, at which the analysis of the temperature distribution, welding thermal cycles and phase shares was performed.
In the calculations, the following are assumed: welding speed v = 0.042 m/min, electrode wire diameter d = 1.2 mm, wire speed ve = 7.8 m/min, the electrode wire temperature Te = 100°C (which is equal to the temperature of the welding head) and TL = 2500°C - temperature at which a drop of molten material is detached from the electrode. The shape of the weld face was determined by a parabola [31] with height hw = 2.77 and width of the reinforcement ww = 11.93 mm. A welding overlap was obtained assuming the distance between axes of beads equal to 8 mm.
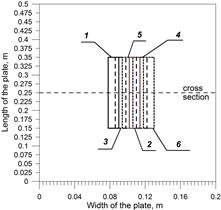
Fig. 3. The scheme of the weld surfaced plate top with the weld padding sequence
In numerical simulation the heat source power 3500 W is used, which corresponds to the welding parameters: voltage U = 24.3 V, current I = 232 A at the efficiency coefficient h = 0.6. In the model of a heat source with the Gaussian distribution corresponding to the action of the electric arc, the following values were adopted: t0 = 0.001 s and z0 = 0.0062 m. The maximum temperature isotherms achieved in the cross-section (x = 0.25 m) during the entire welding process are shown in Figure 4. Isotherms of solidus, A3 and A1 allow one to determine characteristic heat affected zones (Fig. 5). Solidus temperature of 1493°C determines the fusion line, and the temperatures A1 = 720°C and A3 = 835°C determine austenitic transformation zones: partial (between A1 and A3) and full (above A3) - Figure 5. In the figure, the selected cross section points were marked, for which an analysis of the welding thermal cycles and phase transformations were performed.
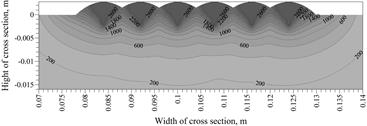
Fig. 4. Maximum temperature field
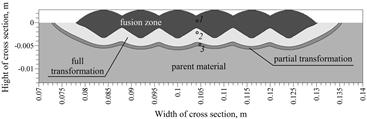
Fig. 5. Cross section with determined heat affected zones
Figures 6-8 present heat cycles in points 1, 2 and 3. In all of the drawings, the peaks illustrate maximum temperatures during subsequent weld beads. In point 1, the temperature of the cast material exceeds the austenitizing temperature during the second and fifth weld beads, and then the material is melted twice during application of these beads.
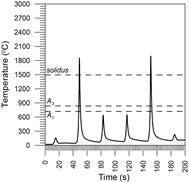
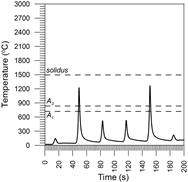
Fig. 6. Thermal welding cycles at point 1 Fig. 7. Thermal welding cycles at point 2
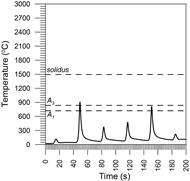
Fig. 8. Thermal welding cycles at point 3
In point 2, the temperature while applying these welds exceeds twice the full austenitizing temperature. In point 3, the material is not melted, but when making a second weld bead, it exceeds the temperature of full austenitization. In weld bead 4, the temperature exceeds the temperature A1 but does not exceed the temperature A3, which leads to incomplete austenite conversion during the fifth weld bead.
The phase transformations kinetics during heating are limited by the temperatures A1 of the beginning and A3 the end of the austenite transformation. In the case of iron and steel casts, mainly continuous cooling diagrams are made, starting slightly above the temperature of A3 and in which the cooling rate is not constant in the range of 800-500°C. A TTT-welding diagram for steel cast 230-450 W is difficult to find. In the calculations, the TTT diagram for S235 steel (Fig. 9) [32] has been adopted, the chemical composition of which is the closest to the 230-450 W cast steel. The initial and end temperatures of phase transformations during cooling on the basis of this diagram have been determined.
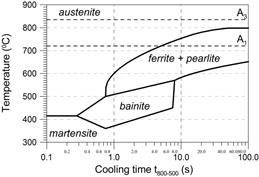
Fig. 9. TTT-welding diagram for S235 steel
The applied computational model allows one to determine the shares of partic-ular phases at any point of the element for any chosen time. After completion of the surfacing process (the material cools) the calculated percentage of bainite in the weld area ranges from 63 to 100% (Fig. 10). The largest share of bainite was determined in areas where single austenitization occurred. In the zones where the secondary austenitization occurred when making subsequent weld beads, the share of bainite amounts to between 60 to 70%.

Fig. 10. Volume fraction of bainite after surfacing
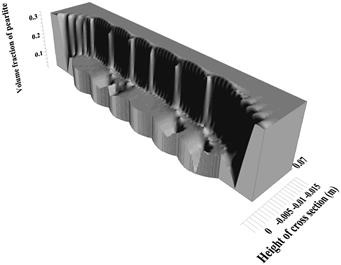
Fig. 11. Volume fraction of pearlite after surfacing

Fig. 12. Volume fraction of ferrite after surfacing
The share of pearlite in the complete transformation zone and fusion zone is 12% and grows to the value of 30% in the incomplete transformation zone in the area of parent material (Fig. 11) and the share of ferrite from 28% in the weld to 70% in the area of parent material (Fig. 12). The changes in phase shares at selected points of the cross section (comp. Fig. 5) are presented in Figures 13-15.
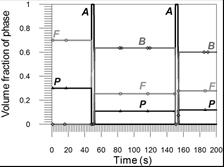
Fig. 13. Volume phase fractions at point 1
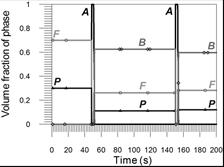
Fig. 14. Volume phase fractions at point 2
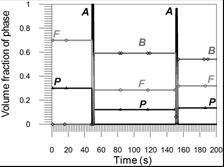
Fig. 15. Volume phase fractions at point 3
5. Conclusions
Overlaying welding is a process during which the melted electrode material is applied to the surface of the welded object constituting a supplementary heat source to the electric arc. This additional heat source must be taken into account in the calculation of the temperature field. In the article, the description of the temperature field in the massive body during the weld surfacing is presented. The total heat source was determined by summing up the thermal radiation of the electric arc and the heat of the molten electrode transferred to the padding weld.
The presented analytical approaches allow for the computation of the volumetric participation of the structural phases during multipass GMAW surfacing or rebuilding of the steel cast. The consequent applied model allows for the determination of HAZ (including full and partial transformation zones, fusion zone), welding thermal cycles, the change of volume phase participations of the structural components, the size and the structural composition of the material in HAZ, the effect of the temperature field on the structural composition during the deposition process at any point of GMAW surfaced object.
The presented model of temperature field and phase change calculation can be used for further analysis of thermal and mechanical states of multi-pass surfaced, hard faced and built up steel casts, amount of other strains, deformations and stresses.
References
[1] Chen, J., Schwenk, C., Wu, C.S., & Rethmeier, M. (2012). Predicting the influence angle on heat transfer and fluid flow for new gas metal arc processes. Int. J. Heat Mass Transf., 55, 102-111.
[2] Fachinotti, V.D., Anca, A.A., & Cardona, A. (2011). Analytical solutions of the thermal field induced by moving double-ellipsoidal and double elliptical heat sources in a semi-infinite body. Int. J. Num. Meth. Biomech. Eng., 27, 595-607.
[3] Heinze, C., Schwenk, C., & Rethmeier, M. (2012). Numerical calculation of residual stress development of multi-pass gas metal arc welding under high restraint conditions. Mat. Design, 35, 201-209.
[4] Joshi, S., Hildebrand, J., Aloraier, A.S., & Rabczuk, T. (2013). Characterization of material properties and heat source parameters in welding simulation of two overlapping beads on a substrate plate. Comp. Mater. Sci., 69, 559-565.
[5] Antonakakis, T., Maglioni, C., & Vlachoudis, V. (2013). Closed form solutions of the heat diffusion equation with Gaussian source. Int. J. Heat Mass Transf., 62, 314-322.
[6] Ghosh, A., Barman, N., Chattopadhyay, H., & Hloch, S. (2013). A study of thermal behaviour during submerged arc welding. Strojniški vestnik - J. Mech. Eng., 59, 333-338.
[7] Fu, G., Lourenco, M.I., Duan, M., & Estefen, S.F. (2014). Effect of boundary conditions on residual stress and distortion in T-joint welds. J. Constr. Steel Res., 102, 121-135.
[8] Franko, A., Romoli, L., & Musacchio, A. (2014). Modelling for predicting seam geometry in laser beam welding of stainless steel. Int. J. Thermal Sci., 79, 194-205.
[9] Salimi, S., Bahemmat, P., & Haghpanahi, M. (2014). A 3D transient analytical solution to the temperature field during dissimilar welding processes. Int. J. Mechn. Sci., 79, 66-74.
[10] Kant, M.A., & Rohr, P.P. (2016). Determination of surface heat flux distributions by using surface temperature measurements and applying inverse techniques. Int. J. Heat Mass Tranf., 99, 1-9.
[11] Kulawik, A., Sczygiol, N., & Wróbel, J. (2016). Determination of stresses in the steel pipe during the superficial heat treatment process with helical path. J. Appl. Math. Comput. Mech., 15(1), 79-86.
[12] Ghosh, A., Yadav, A., & Kumar, A. (2017). Modelling and experimental validation of moving tilted volumetric heat source in gas metal arc welding processes. J. Mater. Process. Tech., 239, 52-65.
[13] Lindgren, L.E., Runnemalm, H., & Näsström, M.O. (1999). Simulation of multipass welding of a thick plate. Int. J. Numer. Meth. Engng., 44, 1301-1316.
[14] Börjesson, L., & Lindgren, L.E. (2001). Simulation of multipass welding with simultaneous computation of material properties. Trans. ASME, 123, 106-111.
[15] Lindgren, L.E., & Hedblom, E. (2001). Modelling of addition of filler material in large deformation analysis of multipass welding. Commun. Numer. Meth. Eng., 17, 647-657.
[16] Deng, D., & Murakawa, H. (2006). Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci., 37, 269-277.
[17] Ramjaun, T.I., Stone, H.J., Karlsson, L., Gharghouri, M., Dalaei, K., Moat, R., & Bhadeshia, H.K.D.H. (2014). Surface residual stresses in multipass welds produced using low transformation temperature filler alloys. Sci. Technol. Weld. Joining, 19, 623-630.
[18] Novotný, L., Abreu, H.F.G., Miranda, H.C., & Béreš, M. (2016). Simulations in multipass welds using low transformation temperature filler material. Sci. Technol. Weld. Join., 21, 680-687.
[19] Sladek, A., Patek, M., & Mician, M. (2017). Behavior of steel branch connections during fatigue loading. Arch. Metal. Mater., 62(3), 1597-1601.
[20] Wang, X.L., Payzant, E.A., Taljat, B., Hubbard, C.R., Keiser, J.R., & Jirinec, M.J. (1997). Experimental determination of the residual stresses in a spiral weld overlay tube. Mater. Sci. Eng., A232, 31-38.
[21] Wojnowski, D., Oh, U.K., & Indacochea, J.E. (2000). Metallurgical assessment of the softened HAZ region during multipass welding. Trans. ASME, 122, 310-315.
[22] Murugan, S., Sanjai, K., Kumar, P.V., Jayakumar, T., Raj, B., & Bose, M.S.C. (2001). Temperature distribution and residual stresses due to multipass welding in type 304 stainless steel and low carbon steel weld pads. Int. J. Pres. Ves. Pip., 78, 307-317.
[23] Kolhe, K.P., & Datta, C.K. (2008). Prediction of microstructure and mechanical of multipass SAW. J. Mater. Process. Techn., 197, 241-249.
[24] Winczek, J. (2010). Analytical solution to transient temperature field in a half-infinite body caused by moving volumetric heat source. Int. J. Heat Mass Transf., 53, 5774-5781.
[25] Winczek, J. (2011). New approach to modeling of temperature field in surfaced steel elements. Int. J. Heat Mass Transf., 54, 4702-4709.
[26] Avrami, M. (1939). Kinetics of phase change. I. General theory. J. Chem. Phys., 7, 1103-1112.
[27] Piekarska, W., Kubiak, M., & Bokota, A. (2011). Numerical simulation of thermal phenomena and phase transformations in laser-arc hybrid welded joint. Arch. Metal. Mater., 56, 409-421.
[28] Koistinen, D.P., & Marburger, R.E. (1959). A general equation prescribing the extent of the auste- nite-martensite transformation in pure iron-carbon alloys and plain carbon steels. Acta. Metal., 7, 59-60.
[29] Piekarska, W., Goszczyńska, D., & Saternus, Z. (2015). Application of analytical methods for predicting the structures of steel phase transformations in welded joints. J. Appl. Math. Comput. Mech., 14(2), 61-72.
[30] Winczek, J., Makles, K., Gucwa, M., Gnatowska, R., & Hatala, M. (2017). Modelling of strains during SAW surfacing taking into heat of the weld in temperature field description and phase transformations. IOP Conf. Series: Materials Science and Engineering (225) 012038 doi:10.1088/1757-899X/225/1/012038.
[31] Hrabe, P., Choteborsky, R., & Navratilova, M. (2009). Influence of welding parameters on geometry of weld deposit bead. In: Int. Conf. Economic Eng. Manufacturing Systems, Brasov, 26-27 November, Regent 10 3(27) 291-294.
[32] Brózda, J., Pilarczyk, J., & Zeman, M. (1983). TTT-welding Diagrams Transformation of Auste- nite. Katowice: Śląsk (in Polish).

