Finding the expected revenues in Markov networks with positive and negative customers at a stationary regime

FINDING THE EXPECTED REVENUES IN MARKOV NETWORKS WITH POSITIVE AND NEGATIVE CUSTOMERS AT A STATIONARY REGIME

Mikhail Matalytski ¹, Dmitry Kopats ²

¹ Institute of Mathematics, Czestochowa University of Technology
Czestochowa, Poland
² Faculty of Mathematics and Computer Science, Grodno State University
Grodno, Belarus
m.matalytski@gmail.com, dk80395@mail.ru

Received: 1 October 2017; Accepted: 1 February 2018

Abstract. Finding the expected revenues in the queueing systems (QS) of open Markov G-networks of two types, with positive and negative customers and with positive customers and signals, has been described in the paper. A negative customer arriving to the system destroys one positive customer if at least one is available in the system, thus reducing the number of positive customers in the system by one. The signal, coming into an empty system (where there are no positive customers), does not have any impact on the network and immediately disappears from it. Otherwise, if the system is not empty, when it receives a signal, the following events can occur: the incoming signal instantly moves the positive customer from one QS into another with a certain probability, or with the other probability, the signal is triggered as a negative customer.

MSC 2010: 60-08, 60J20, 60J25, 60J27, 60K10

Keywords: G-network, positive and negative customers, signals, expected revenues, stationary regime

1. Introduction

Queueing systems with revenues at a stationary regime were introduced into consideration in [1], but networks were introduced in [2]. The review of the results obtained by the systems and queueing networks (QN) at a stationary regime are contained in [3]. They are devoted to finding the mean revenues in the network systems that depend only on their states and do not depend on the time and solved the problem of finding the optimal service rates of customers in QS by the dynamic programming method. Revenues from transitions between network states were not considered. QN, with revenues at a non-stationary regime, have been studied in [4, 5]. In such a network, in the transition of a positive customer of QS to another, the last customer gets some generally random revenue, and the revenue of the first QS is reduced accordingly by that amount. Revenues from transitions between network states were either depending on the QN state and time, or were a random variable (RV) with specified moments of the first and second orders. In review paper [6] in the monograph [7], the results of research, optimization and selection of the optimal management strategies in Markov networks with the revenues are presented, various applications of management strategies as probability forecasting models of the expected revenues in information and telecommunication systems and networks (for instance, when service requests on the server brings revenue to service company), insurance companies, logistics transportation systems, industrial systems and other facilities are described.

As it is known, any Markov QN functioning can be described by the Markov chain with continuous time and with a larger or countable number of states. The sim- plest case of Markov chain with a small number of states and constant revenues from the transitions between states has been considered in the monograph [8].

In recent years, attention has been paid to the study of Markov chains with revenues and various features: with bounded waiting time of claims and unreliable QS [9-11]. Time-dependent expressions for the expected revenues have been obtained. However, this was done with one important limitation: QS should have been able to operate in a heavy-traffic regime, i.e. at any time in the QS it should serve at least one customer. The current paper covers a Markov network with revenues, positive and negative customers, as well as with signals, in the case when revenues from transitions between network states are random variables (RV) with given mean values; this restriction was removed. Expressions for finding expected revenues in the network systems in a unit time at a stationary regime have been derived.

It should be noted that Markov QN with positive and negative customers (without revenues) were introduced by E. Gelenbe [12] as models of behavior of computer viruses in the information and telecommunication systems and networks and are called G-networks. In the same paper, the condition of existence of a stationary regime is presented. The paper shows that, as for almost all Markov chains, the stationary distribution of probabilities has a multiplicative form.

Markov networks with positive customers and signals were introduced in [13] and investigated at a stationary regime. The action of signals consists in immediately moving a positive customer with a specified probability of the system into some other network system.

The signal can work as a trigger, which does not destroy the customer, but only moves it immediately with a given probability from one system to another network system as a negative customer. Signals (triggers) are used to control the load in the network.

Consider an open queueing G-network with single-line QSs. An incoming flow of positive (regular) customers with rate (intensity) and Poisson flow of negative customers with rate , are coming into QS from the out- side (from QS ). All flows of customers entering the network are independent. The service time of the positive customers in the QS is exponentially distributed with the rate , . A negative customer, arriving to some QS in which there is at least one positive customer, instantly destroys (deletes, removes from the network) one of customers. On the assumption of an exponential distribution of service time of positive customers, we would not care about what exact customer is destroyed [13]. After that, positive customer immediately leaves out the network without any servicing by the QS. Thus, each QS of the network can serve only regular customers.

The positive customer, serviced by at moment time , with the probability is sent to QS as a positive customer, with probability - as a nega- tive customer, and with probability the customer leaves the network to the external environment (QS ), . By the network state we mean a vector of dimension , where - the count of customers in the system at time t, . Processes , , , are Markov chains with continuous time and a countable number of states. We will assume that Markov chain is ergodic, having a stationary distribution,

2. Analysis of the expected revenues in a network with positive and negative customers when the revenues from the network transitions between the states are given random variables with given mean values

Let RV - service time of the customer by the system , distributed expo- nentially with the distribution function Let’s consider the dynamics of revenue changes of the i-th system. Let at the initial time the revenue of QS is equal to ; - revenue of the i-th QS at time t, if at the initial time the network was at state k. The revenue of its QS at moment time can be represented as

.

(1)

To find the revenues of QS , specify the conditional probabilities of the events that may occur during , . The following cases are possible:

1) a positive customer will come to the i-th QS from the external environment with probability , it will bring a revenue of the amount , where - RV with expected value (E) , ;

2) a negative customer will come to QS from the external environment with probability , it will bring a loss of the amount , - RV with , ;

3) a positive customer after servicing by the i-th system will come out of the network to the external environment with probability , a revenue of the i-th QS will decrease by an amount , where - RV with , - Heaviside function,;

4) a positive customer will move from the i-th QS to the j-th QS with probability , , ; a revenue of the i-th QS will decrease by an amount , and revenue of the j-th QS will increase by this amount, , ;

5) a positive customer will move to the i-th QS with probability , a revenue of the i-th QS will increase by an amount , and revenue of the j-th QS will decrease by this amount, , , ;

6) a positive customer, after finishing the service by the i-th QS, will move to the j-th QS as a negative customer with probability , by such a transition, a revenue of the i-th QS will decrease by an amount , - RV with ,

7) no state changes of the i-th system will happen on the time interval with probability , , ;

8) the i-th system at each small time interval will increase its revenue by the amount of (due to servicing some customers), - RV with , .

From the aforesaid follows

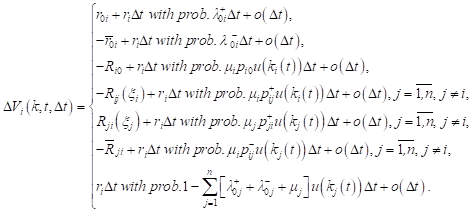(2)

We find the expression for the change of expected revenue in i-th QS at time t. According to (2), the following can be written for the expected value:

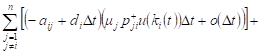
(3)

Therefore, as it follows from (1), (3),

(4)

Integrating both sides of (4) from 0 to t:

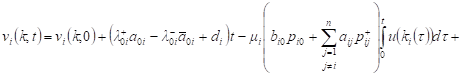
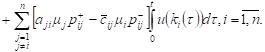(5)

Obviously, - total time during which on the interval of time customers count in the i-th QS is more than zero. Because the is an ergodic stationary random process, is also ergodic process as a real measur- able function of an ergodic process [14]. Therefore

,

(6)

where - customers count in the i-th QS at a stationary regime.

Value characterizes the expected revenue of the i-th QS at a unit of time at a stationary regime. Then, dividing both sides of (5) by t, tends t to infinity, and because of (6) we shall have:

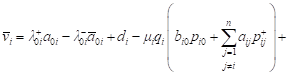
(7)

The E. Gelenbe paper [12] shows that values are found by solving the following system of nonlinear equations:

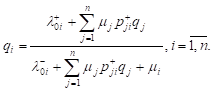(8)

For comparison, we give the relation for the value of revenue (7) of the i-th QS in the case when in the network there are no negative customers [6, 7], which we denote by :

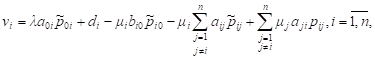
where: - the intensity of the incoming simplest flow of customers (arriving rate) to the network; - arrive probability to the i-th QS, - probability that a positive customer, served by , moves to QS as a positive customer, - probability that, a customer leaves the network to the external environment,

Let’s find the difference Note that and Taking into account the expressions for we obtain

.

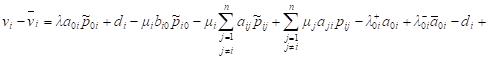
i.e. presence of the negative customers reduces the revenues of QS by this amount.

3. Analysis of the expected revenues in a network with positive customers and signals

Consider now a G-network with positive customers and signals [13, 15]. Network description is given in [2, 3]. The signal, coming in an empty system (in which there are no positive customers), does not have any impact on the network and immediately disappears from it. Otherwise, if the system is not empty, when it receives a signal, the following events can occur: incoming signal instantly moves the positive customer from the system into the system with probability , in this case, the signal is referred to as a trigger; or with probability the signal is triggered by a negative customer and destroys in QS the positive customer. The state of the network defined by the vector , where - the customers count at the moment of time at the system , .

To find the revenues of the i-th QS, we write the conditional probabilities of the events that may occur during , . The following cases are possible:

– a signal will arrive to the i-th QS from the external environment with probability ; it will trigger as a negative customer and will destroy a positive customer in QS , that will bring a loss in an amount , - RV with , ;

– signal arriving to QS will immediately move a positive customer from system to system with probability, , ; by such a transition a revenue of the i-th QS will decrease by an amount , revenue of the j-th QS will increase by this amount, where - RV with , ;

– a customer from system will move to QS as signal, if there were no customers, with probability , by such a transition a revenue of the i-th QS will decrease by an amount , - RV with , ;

– a positive customer after finishing the service in QS will move to QS as a signal, which is triggered as negative customer, will destroy in QS a positive customer; the probability of this event is ; by such a transition a revenue of will decrease by an amount , and a revenue of will decrease by this amount, , , ;

– a positive customer after finishing the service by QS will move to QS as a signal, which will immediately move a positive customer from system to system ; the probability of this event is , , ,; by such a transition a revenue of the i-th QS and system will decrease by an amount , and for the system will increase by this amount, where – RV with , , , ;

– the network state will not change on the interval with probability .

The revenue changes of on the interval may be written as

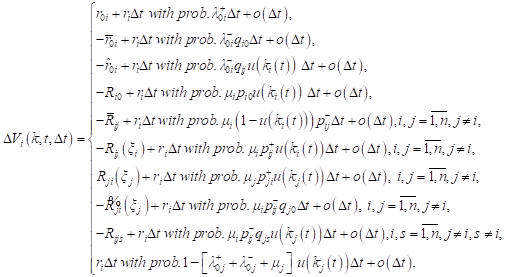(9)

Taking into account (9), for the expected value of the revenue changes can be written:

, .

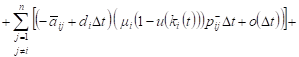
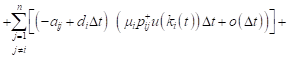
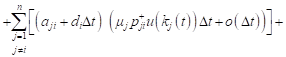
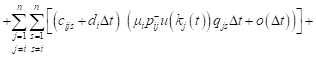
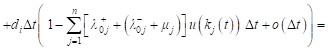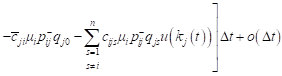Then, similarly as in (4), for the expected revenue of the system S_i with positive customers and signals, we obtain

,

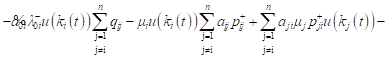
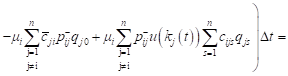
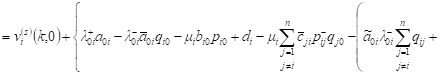
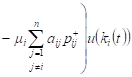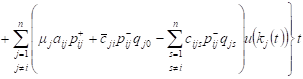(10)

Having integrated both sides (10) from 0 to t we obtain:

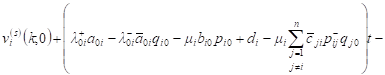
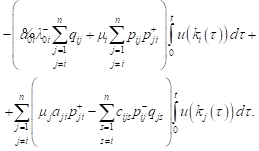Dividing both sides of expression by t and using the relation , where , similarly as in the preparation of equality (6), but only for the network with positive customers and signals - this is stationary probability that the i-th QS is not empty, can obtain relation for the expected revenue of the i-th QS of the considered network per unit time at a stationary regime:

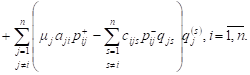Finding the stationary probabilities , has been described in [13, 15].

Similarly, as previously, differences could be found, which show how much the existence of signals reduces network revenues.

4. Conclusions

A Markov queueing network with revenues, positive and negative customers, and also signals, in the case when revenues from transitions between network states are RV with given mean values, has been carried out. Relations for finding the expected revenues in the network systems per unit time at a stationary regime have been derived.

Further investigations may be related to finding network systems revenue variances, and also clarifying for what revenue functions, expected revenues will take similar values. It is also possible to generalize obtained results for the case when arrival rates of positive and negative customers, service rates of positive customers, depend on network states and time.

References

[1] Crabill, T. (1972). Optimal control of a service facility with variable exponential service times and constant arrival rate. Management Science, 18, 560-566.

[2] Foschini, G. (1977). On heavy traffic diffusion analysis and routing in packet switched networks. Computer Performance, 9, 499-514.

[3] Stidham, S., & Weber, R. (1993). A survey of Markov decision models for control of networks of queue. Queueing Systems, 3, 291-314.

[4] Matalytski, M., & Pankov, A. (2003). Analysis of stochastic model of the changing of incomes in the open banking network. Vestnik GrSU, 3, 5, 19-29.

[5] Matalytski, M., & Pankov, A. (2003). Incomes probabilistic models of banking network. Scientific Research of the Institute of Mathematics and Computer Science of Czestochowa University of Technology, 11, 2, 99-104.

[6] Matalytski, M. (2009). On some results in analysis and optimization of Markov networks with incomes and their application. Automation and Remote Control, 70, 10, 1683-1697.

[7] Koluzaeva, E., & Matalytski, M. (2011). Analysis and Optimization of Queueing Networks. Saarbrucken: LAPLAMBERT Academic Publishing.

[8] Howard, R. (1964). Dynamic Programming and Markov Processes. Moscow: Soviet Radio.

[9] Matalytski, M. (2015). Analysis and forecasting of expected incomes in Markov network with bounded waiting time for the claims. Automation and Remote Control, 76, 6, 1005-1017.

[10] Matalytski, M. (2015). Analysis and forecasting of expected incomes in Markov network with unreliable servicing systems. Automation and Remote Control, 15, 11, 2179-2189.

[11] Matalytski, M., & Naumenko, V. (2016). Stochastic Networks with Non-Standard Customers Movement. Grodno: GrSU.

[12] Gelenbe, E. (1991). Product form queuing networks with negative and positive customers. Journal of Applied Probability, 28, 656-663.

[13] Gelenbe, E. (1993). G-networks with triggered customer movement. Journal of Applied Probability, 30, 742-748.

[14] Prokhorov, Y.V., & Rozanov, U.A. (1973). The Theory of Probability. Moscow: Science.

[15] Bocharov, P.P., & Vishnevsky, V.M. (2003). G-networks: the development of the theory of multiplicative network. Automation and Remote Control, 5, 46-74.