Recurrence relations for two-channel closed queueing systems with Erlangian service times
Bohdan Kopytko
,Kostiantyn Zhernovyi
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
RECURRENCE RELATIONS FOR TWO-CHANNEL CLOSED QUEUEING SYSTEMS WITH ERLANGIAN SERVICE TIMES
Bohdan Kopytko 1, Kostiantyn Zhernovyi 2
1
Institute of Mathematics, Czestochowa University of Technology
Czestochowa, Poland
2 Educational and Scientific Institute, Banking University, Lviv,
Ukraine
bohdan.kopytko@im.pcz.pl, k.zhernovyi@yahoo.com
Received: 12 December 2017;
Accepted: 26 January 2018
Abstract. This paper proposes a method for determining the steady-state characteristics of two-channel closed queueing systems with an exponential distribution of the time generation of service requests and the Erlang distributions of the service times. Recurrence relations for computing the steady-state distribution of the number of customers in the system are deduced. The obtained algorithms are tested on examples using simulation models in the GPSS World environment.
MSC 2010: 60G10, 60J28, 60K25, 93B40
Keywords: two-channel closed queueing system, Erlangian service times, fictitious phase method, recurrence relations
1. Introduction
Closed queueing systems are widely used as models to evaluate characteristics of the information systems, data networks and queueing processes in production, transport, trade, logistics and service systems [1]. The closed system is also called the system with a finite number of sources or the Engset system.
Suppose that a two-channel queueing system
receives service requests from ![]() identical sources.
Each source is alternately on and off. A source is off when it has a service
request being served, otherwise the source is on. A source in the on-state
generates a new service request after an exponentially distributed time (the
genera-
tion time) with mean
identical sources.
Each source is alternately on and off. A source is off when it has a service
request being served, otherwise the source is on. A source in the on-state
generates a new service request after an exponentially distributed time (the
genera-
tion time) with mean ![]() The sources act independently of each
other. The service time of a service request has the Erlang
distribution. A service request, that is
generated when two channels are occupied, waits in the queue.
The sources act independently of each
other. The service time of a service request has the Erlang
distribution. A service request, that is
generated when two channels are occupied, waits in the queue.
To investigate the systems with Erlangian
service times, in particular the M/En/1/∞ system
[2], the method of fictitious phases, developed by A.K. Erlang [3], was
applied. The Erlangian service times of the order ![]() means
that each
customer runs sequentially
means
that each
customer runs sequentially ![]() service phases, the
duration of which is distributed
exponentially with parameters
service phases, the
duration of which is distributed
exponentially with parameters ![]() respectively.
respectively.
The objective of this work is the
construction with the help of fictitious phase method recursive algorithms for
computing the steady-state distribution of the number of customers in two-channel closed
queueing systems with an exponential distribution of
the time generation of service requests and Erlangian service times of the order ![]() and
and ![]() A similar approach is used in [4, 5], where recur-
sive algorithms are developed for the systems M/E2/2/m,
M/E2/2/∞, M/E2/3/m
and M/E2/3/∞ as well as
for the systems of the same types with threshold and hysteretic strategies of
the random dropping of customers.
A similar approach is used in [4, 5], where recur-
sive algorithms are developed for the systems M/E2/2/m,
M/E2/2/∞, M/E2/3/m
and M/E2/3/∞ as well as
for the systems of the same types with threshold and hysteretic strategies of
the random dropping of customers.
2. The system with Erlangian service times of the second order
Suppose that the service time of each
customer is distributed under the generalized Erlang law of the order ![]() , that is, the service time is the sum
of
, that is, the service time is the sum
of ![]() independ-
ent random variables exponentially
distributed with parameters
independ-
ent random variables exponentially
distributed with parameters ![]() respectively.
respectively.
Let ![]() denote the number of customers in the system and let
denote the number of customers in the system and let ![]() be the number of busy channels. In accordance with the
method of phases, let us enumerate the system’s states as follows:
be the number of busy channels. In accordance with the
method of phases, let us enumerate the system’s states as follows: ![]() corresponds to the empty system;
corresponds to the empty system; ![]() is the state, when
is the state, when ![]() and the service occurs in the phase
and the service occurs in the phase ![]() ;
; ![]() is the state, when
is the state, when ![]() and the services occur in the phase
and the services occur in the phase ![]() and
and ![]() respectively. We denote by
respectively. We denote by ![]() and
and ![]() respectively, steady-state probabilities that the system is
in the each of these states. Assuming that
respectively, steady-state probabilities that the system is
in the each of these states. Assuming that ![]() and
and ![]() to calculate the steady-state
probabilities, in the case of
to calculate the steady-state
probabilities, in the case of ![]() we obtain the system
of equations:
we obtain the system
of equations:
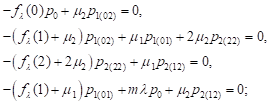 | (1) |
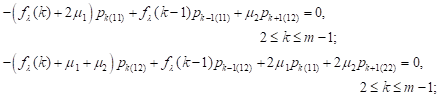 | (2) |
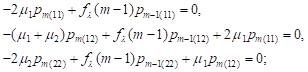 | (3) |
| (4) |
Introducing the notation
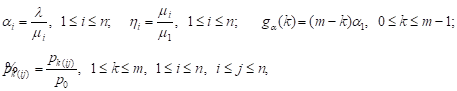 |
and using equations (1), we find:
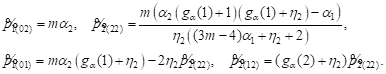 | (5) |
From equations (2), we obtain the recurrence relations:
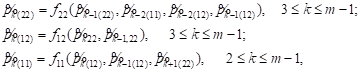 | (6) |
where:
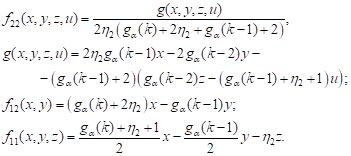 |
Using equations (3) we find:
 | (7) |
Recurrence
relations (5)-(7) allow us to consistently calculate ![]()
![]() and
and ![]() Using the normalization condition (4),
we find steady-state probabilities by the
formulas
Using the normalization condition (4),
we find steady-state probabilities by the
formulas
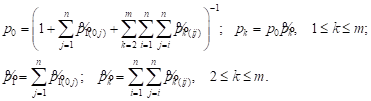 | (8) |
Here ![]() and
and ![]() is the steady-state probability that
is the steady-state probability that ![]() We calculate the steady-state
characteristics - the average number of customers in the system
We calculate the steady-state
characteristics - the average number of customers in the system ![]() the average queue length
the average queue length ![]() and average waiting time
and average waiting time ![]() - by the formulas
- by the formulas
Here ![]() is a steady-state value of the arrival rate of customers,
defined by the equality
is a steady-state value of the arrival rate of customers,
defined by the equality
The
parameter ![]() is a characteristic of the system
capacity, because for the steady-state regime we have the equality of the
intensities of flows of customers
arriving and served.
is a characteristic of the system
capacity, because for the steady-state regime we have the equality of the
intensities of flows of customers
arriving and served.
3. The system with Erlangian service times of the third order
To calculate the steady-state probabilities,
in the case of ![]() we obtain the system of
equations:
we obtain the system of
equations:
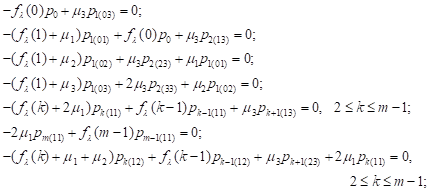
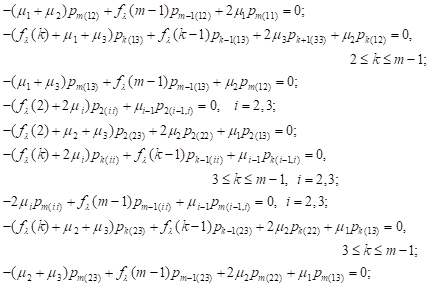 | (9) |
| (10) |
Introducing the notation ![]() and using equations (9) we find:
and using equations (9) we find:
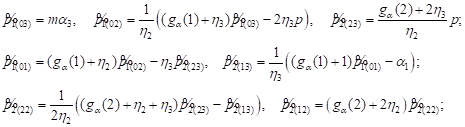
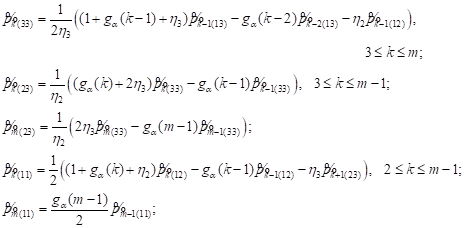
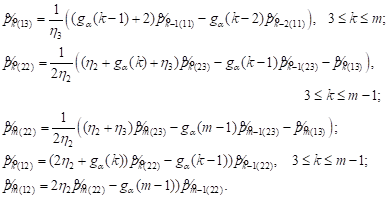 | (11) |
Recurrence
relations (11) allow us to calculate ![]() and consistently obtain
the expression for
and consistently obtain
the expression for ![]()
![]() and
and ![]() as linear functions of the
unknown parameter
as linear functions of the
unknown parameter ![]() To find
To find ![]() we use any of the equations
we use any of the equations
| (12) |
Equations (12) were not involved in obtaining (11). Using the normalization condition (10), we find the steady-state probabilities by (8).
4. The system with Erlangian service times of n-th order
To calculate the steady-state probabilities
in the case of ![]() , we obtain
the system of equations:
, we obtain
the system of equations:
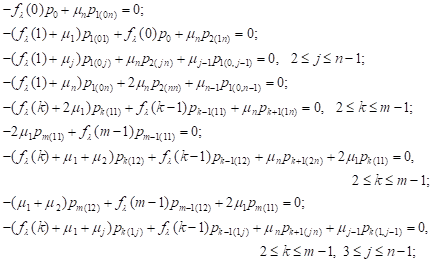 (13) (13)
 |
| (14) |
Introducing the notation ![]() and using equations (13) we find:
and using equations (13) we find:
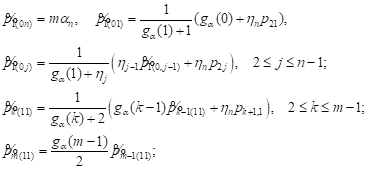
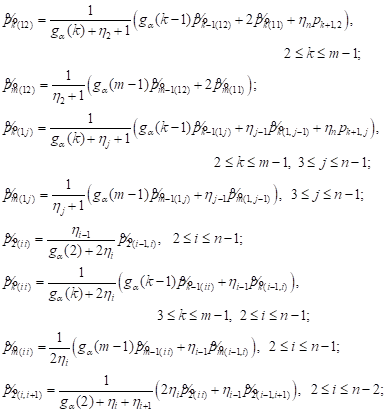 |
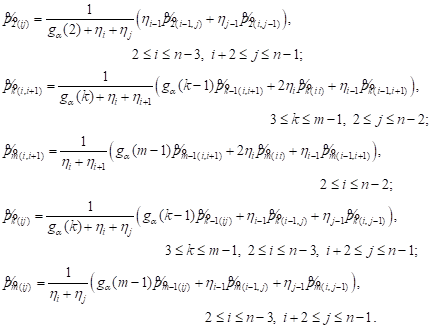 | (15) |
Recurrence relations (15) allow us to calculate ![]() and consistently obtain
the expression for
and consistently obtain
the expression for
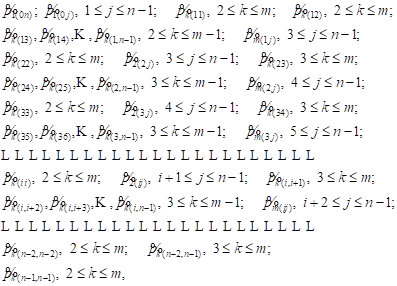 |
as linear
functions of the unknown parameters ![]() To deter-
mine
To deter-
mine ![]() we use system of
we use system of ![]() equations
equations
 (16) (16)
|
Equations (16) as well as the equation
were not involved in obtaining (15). Using the normalization condition (14), we find the steady-state probabilities by (8).
5. Numerical example
Consider a two-channel closed queueing system with an exponential distribution of the time generation of service
requests and Erlangian service times of
the order ![]() for the following values of the
parameters:
for the following values of the
parameters: ![]()
![]()
![]()
![]()
The values of the steady-state
characteristics of the system, found using
the recurrence relations obtained in this paper, are presented in Tables 1
and 2.
In order to verify the obtained values, the tables contain the computing
results
obtained with the help of the GPSS World simulation system [6] for the time
value ![]()
Table 1
Stationary distribution of the number of customers in the system
|
k |
Values of the steady-state probabilities pk |
|
|
Recurrence method |
GPSS World |
|
|
0 |
0.000004 |
0.000004 |
|
1 |
0.000055 |
0.000053 |
|
2 |
0.000440 |
0.000461 |
|
3 |
0.002605 |
0.002620 |
|
4 |
0.011830 |
0.011963 |
|
5 |
0.040833 |
0.040495 |
|
6 |
0.105048 |
0.104882 |
|
7 |
0.196206 |
0.196322 |
|
8 |
0.256876 |
0.256441 |
|
9 |
0.224423 |
0.224365 |
|
10 |
0.121478 |
0.122119 |
|
11 |
0.035863 |
0.036016 |
|
12 |
0.004340 |
0.004259 |
Table 2
Stationary characteristics of the system
|
Method |
E(nc) |
E(Q) |
E(W) |
λav |
|
Recurrence |
8.000127 |
6.000191 |
1.500095 |
3.999873 |
|
GPSS World |
8.002 |
6.001 |
1.500 |
– |
6. Conclusions
The numerical algorithm for solving a system
of equations for steady-state probabilities, developed in this article, is
based on the presence of three or four
unknowns in most equations. The constructed recurrence relations are used for
the direct calculation of the steady-state probabilities, that allows us to
reduce
the amount of calculations in comparison with the case of application of the
direct or iterative classical methods. Using the obtained recurrence relations
makes it
possible in the case of ![]() to directly
calculate the steady-state probabilities,
in the case of
to directly
calculate the steady-state probabilities,
in the case of ![]() to reduce the system of
equations for the steady-state probabilities for a single linear equation for the unknown parameter
to reduce the system of
equations for the steady-state probabilities for a single linear equation for the unknown parameter ![]() and in the case of
and in the case of ![]() to reduce the number of solved equations
from
to reduce the number of solved equations
from ![]() to
to ![]()
References
[1] Nesterov, Yu.G. (2014). Analysis of characteristics of a closed queuing system with relative priorities. Nauka i Obrazovanie. MGTU im. N. Baumana, 3, 242-254 (in Russian).
[2] Bocharov, P.P., & Pechinkin, A.V. (1995). Queueing Theory. Moscow: RUDN (in Russian).
[3] Brockmeyer, E., Halstrøm, H.L., & Jensen, A. (1948). The Life and Works of A.K. Erlang. Copen- hagen: Danish Academy of Technical Sciences.
[4] Zhernovyi, K.Yu. (2017). Determining stationary characteristics of two-channel queueing systems with Erlangian distribution of service time. Cybernetics and Systems Analysis, 53, 1, 92-104.
[5] Kopytko, B., & Zhernovyi, K. (2016). Steady-state characteristics of three-channel queueing systems with Erlangian service times. Journal of Applied Mathematics and Computational Mechanics, 15(3), 75-87.
[6] Zhernovyi, Yu. (2015). Creating Models of Queueing Systems Using GPSS World. Saarbrücken: LAP Lambert Academic Publishing.

