Note on traces of matrix products involving inverses of positive definite ones
Andrzej Z. Grzybowski
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
NOTE ON TRACES OF MATRIX PRODUCTS INVOLVING INVERSES OF POSITIVE DEFINITE ONES
Andrzej Z. Grzybowski
Institute of Mathematics, Czestochowa
University of Technology
Czestochowa, Poland
andrzej.grzybowski@im.pcz.pl
Received: 1 December 2017;
Accepted: 7 February 2018
Abstract. This short note is devoted to the analysis of the trace of a product of two matrices in the case where one of them is the inverse of a given positive definite matrix while the other is nonnegative definite. In particular, a relation between the trace of A–1H and the values of diagonal elements of the original matrix A is analysed.
MSC 2010: 15A09, 15A42, 15A63
Keywords: matrix product, trace inequalities, inverse matrix
1. Introduction
Traces of matrix products are of special interest and have a wide range of appli- cations in different fields of science such as economics, engineering, finance, hydro- logy and physics. They also arise naturally in the applications of mathematical sta- tistics, especially in regression analysis, [1-3] or the analysis of discrete-time statio- nary processes [4]. There are papers devoted to the role of matrix-product-traces in the description of the probability distributions of quadratic forms of random vectors, [1, 5], or to the development of approximate boundaries for their (i.e. product traces) values [6-11]. In some statistical applications the product under consideration involves inverse A–1 of a given positive definite matrix A. In particular, it takes place in the Bayesian analysis in regression modelling, where the matrix A can be interpreted as the covariance matrix of the disturbances and/or a priori distribution of unknown system-parameters [2, 3].
In this paper, we present an equation concerning traces of certain matrix products involving an inverse A–1 of a given matrix A, and next this equation is used to obtain a result relating the changes in the values of the diagonal elements of the original matrix A with the values of the considered trace. This note is organized as follows. In the next section we recall some definitions and facts that will be necessary to state and prove the new results. In Section 3, we state the main equation and then, in Section 4 we present some possible applications.
2. Preliminary definitions, facts and notation
All of the matrices considered here are
real. For any square matrix A = [aij]n´n the symbol ![]() denotes the
cofactor of the element aij, and adj(A) denotes the transpose
of a matrix with elements being the cofactors of appropriate elements
of A, i.e. adj(A) = [
denotes the
cofactor of the element aij, and adj(A) denotes the transpose
of a matrix with elements being the cofactors of appropriate elements
of A, i.e. adj(A) = [![]() ]T.
]T.
For any square matrix A we write A > 0 (or A ³ 0) if the matrix is positive definite (or positive semi-definite), i.e. A is symmetric and xTAx > 0 for all nonzero column vectors xÎRn (or xTAx ³ 0 for all xÎRn). A square matrix is nonnegative definite if it is positive definite or a positive semi-definite one.
The following facts concerning determinants and/or inverses of matrices expressed in so-called block forms can be found in various textbooks, see e.g. [12, pp. 33-34].
Fact 1.
Let A = [aij]k´k and x be a k-dimensional column vector. Then for any number a
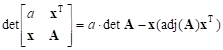 | (1) |
Fact 2.
Let A and B be symmetric matrices. The following equality is true, provided that the inverses that occur in this expression do exist
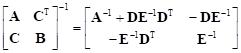 | (2) |
with matrices D and E being defined as follows: D = A–1CT and E = B – CA–1CT.
Fact 3.
Let A be nonsingular and let u, v be two column vectors with dimensions equal to the order of A. Then
| (3) |
This useful equation gives a method of computing the inverse of the left-hand side of (3) knowing only the inverse of A.
Definition (Hadamard Product). If A = [aij]n´m and B = [bij]n´m are the matrices of the same dimensions nxm, then their Hadamard product is the nxm - matrix А*В of elementwise products, i.e. А*В = [aij·bij]n´m
We have the following results involving Hadamard products.
Fact 4.
For any square matrices A, B of the same order, the following equality holds:
| Tr AB = eT | (A*BT) e (4) |
with e being the vector of an appropriate dimension with all coefficients equal to unity, i.e. eT = (1,1,..,1).
Schur’s lemma. Let A and B be square matrices of the same order. If these matrices are both nonnegative definite then their Hadamard product А*В is also nonnegative definite.
3. The main result
Let us consider a square symmetric matrix of order k given in the following block-form
A = 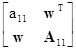 | (5) |
Let matrix C have the following block-form:
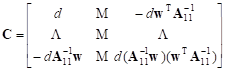 | (6) |
where the constant d equals ![]()
Proposition 1
Let A > 0 and H ³ 0. Let A11 and H11 be the submatrices obtained by deleting the first row and the first column in A and H, respectively. Then the matrix C given by (6) is positive definite, the constant d in (6) is a positive one, and
| Tr(A–1H) – Tr( | (7) |
Proof.
Let us note that a11 > 0 and det(A11) > 0 (it is because A > 0). Thus the inverse of A can be computed with the help of the Facts 1, 2. Indeed, let us express the matrices D, E that appears in formula (2) using the objects from the matrix given in (5):
D = wT/a11 and
E = ![]() – wwT/a11
– wwT/a11
Now, by (2), the inverse of the block matrix takes on the form
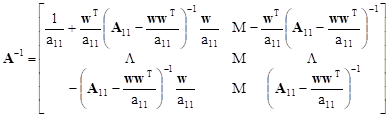 | (8) |
It results from the Fact 3 that we have the following equality for lower-right block in (8):
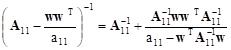 | (9) |
Taking the formula (9) into account we can obtain new forms for the remaining three blocks in (8). The first one, in the upper left corner (as a matter of fact 1x1 matrix), takes on the following form:
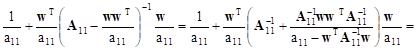
![]()
![]()
![]()
![]()
The second block in the first row can be transformed in the following way:
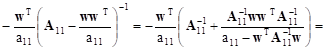
![]()
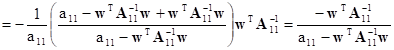
Similarly the third one takes on the form:
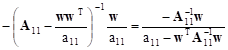 |
Now the matrix A–1 can be expressed by the following simple formula:
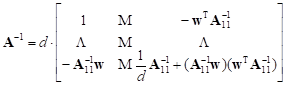 = =
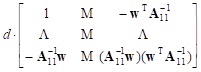 + + 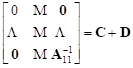 | (10) |
Thus, for any matrix H of an appropriate dimension the following equalities hold:
| Tr(A–1H)
= Tr(CH + DH) = Tr(CH) + Tr(DH) = Tr(CH) + Tr( |
Now we show that the number d is positive.
Indeed, in view of Fact 1 we have:
![]()
But ![]() , so
we finally have:
, so
we finally have:
![]()
Since the matrix A is positive definite one, both above determinants are positive and this yields the positivity of d:
![]()
To complete the proof we need to show that the matrix C is positive definite one. For an arbitrary k-dimensional vector xT = (x1,x2T), x1ÎR, x2ÎRk–1 we have
| xT C x = d (x1 – b)2,
with b = |
This yields that for any nonzero vector xÎRk, xT C x > 0 and thus the matrix C is positive definite.
The proof of Proposition 1 is completed.
4. Some applications
First we state a proposition which is a quite straightforward conclusion from Proposition 1.
Proposition 2
Let the matrices A, H satisfy the assumptions from Proposition 1, and let, as previously indicated, symbols A11 and H11 denote the submatrices obtained by deleting the first row and the first column in A and H, respectively. Then
| tr(A–1H) – tr( |
Proof.
From Proposition 1 we know that Tr(A–1H) – Tr(![]() H11) = Tr CH and that C
is a positive definite matrix. From Fact 4 we have:
H11) = Tr CH and that C
is a positive definite matrix. From Fact 4 we have:
| Tr(CH) = eT (C*HT) e |
By the assumptions matrix H is nonnegative definite, thus HT is also nonnegative definite. From nonnegative definiteness of the matrices C and HT it follows, in the light of the Schur’s lemma, that C*HT is nonnegative definite as well, and consequently eT (C*HT) e ³ 0. This fact completes the proof.
Let us consider now a symmetric positive
definite matrix A = [aij]. Let us define a
matrix Ax = [aij] related with A by the formula: a11 = a11 – f(x) and aij = aij for all remaining elements of A,
where![]() , DÍR, is a given real function.
, DÍR, is a given real function.
Proposition 3
Let A > 0 and H ³ 0 be
square matrices of the same order. Let f be a function differentiable on
an interval D such that Ax > 0 for
all xÎD. Let for all xÎD, a function ![]() be defined as T(x) = Tr(
be defined as T(x) = Tr(![]() ). Then T is nondecreasing (non-
increasing) if and only if f is nondecreasing (nonincreasing).
). Then T is nondecreasing (non-
increasing) if and only if f is nondecreasing (nonincreasing).
Proof.
It follows from Proposition 1 that
| T(x) = Tr( |
where
![]()
While the matrix C and constant d are defined in (6).
Note that the function T depends on its argument only thru the function D. Now a little calculation shows that for each xÎInt(D) the derivative of T does exist and can be expressed in the following form:
![]()
In view of the assumptions about the matrices
A and H and our previous results, the ratio ![]() is nonnegative, which completes the
proof.
is nonnegative, which completes the
proof.
5. Conclusions
Due the fact that in our results the matrix H is nonnegative definite, one may consider matrices of the form H = wwT, with w being a column vector. Because of the well-known relation wAwT = Tr(AwwT), it is easy to see that the above results can be also used for the analysis of the quadratic forms wAwT with A being a given symmetric positive definite matrix.
References
[1] Bao, Y., & Ullah, A. (2010). Expectation of quadratic forms in normal and nonnormal variables with applications. Journal of Statistical Planning and Inference, 140(5), 1193-1205.
[2] Berger, J.O. (1985). Statistical Decision Theory and Bayesian Analysis. New York: Springer-Verlag.
[3] Grzybowski, A. (2002). Metody wykorzystania informacji a priori w estymacji parametrów regresji. Seria Monografie No 89. Częstochowa: Wydawnictwo Politechniki Częstochowskiej, 153 (in Polish).
[4] Ginovyan, M.S., & Sahakyan, A.A. (2013). On the trace approximations of products of Toeplitz matrices. Statistics and Probability Letters, 83, 753-760.
[5] Magnus, J.R. (1979). The expectation of products of quadratic forms in normal variables: the practice. Statistica Neerlandica, 33, 131-136.
[6] Chang, D.-W. (1999). A matrix trace inequality for products of Hermitian matrices. Journal of Mathematical Analysis and Applications, 237, 721-725.
[7] Fang, Y., Loparo, K.A., & Feng, X. (1994). Inequalities for the trace of matrix product. IEEE Transactions On Automatic Control, 39, 12.
[8] Furuichi, S., Kuriyama, K., & Yanagi, K. (2009). Trace inequalities for products of matrices. Linear Algebra and its Applications, 430, 2271-2276.
[9] Komaroff, N. (2008). Enhancements to the von Neumann trace inequality. Linear Algebra and its Applications, 428, 738-741.
[10] Patel, R., & Toda, M. (1979). Trace Inequalities Involving Hermitian Matrices. Linear Algebra and its Applications, 23, 13-20.
[11] Wang, B.-Y., Xi, B.-Y., & Zhang, F. (1999). Some inequalities for sum and product of positive semidefinite matrices. Linear Algebra and its Applications, 293, 39-49.
[12] Rao, C.R. (1973). Linear Statistical Inference and Its Applications. New York: John Wiley & Sons.

