The fundamental solutions to the central symmetric time-fractional heat conduction equation with heat absorption

THE FUNDAMENTAL SOLUTIONS TO THE CENTRAL SYMMETRIC TIME-FRACTIONAL HEAT CONDUCTION EQUATION WITH HEAT ABSORPTION

Yuriy Povstenko¹, Joanna Klekot ²

¹Institute of Mathematics and Computer Science, Faculty of Mathematical and Natural Sciences, Jan Długosz University in Częstochowa
Częstochowa, Poland
²Institute of Mathematics, Częstochowa University of Technology
Czestochowa, Poland
j.povstenko@ajd.czest.pl, joanna.klekot@im.pcz.pl

Received: 8 March 2017; accepted: 12 June 2017

Abstract. The time-fractional heat conduction equation with heat absorption proportional to temperature is considered in the case of central symmetry. The fundamental solutions to the Cauchy problem and to the source problem are obtained using the integral transform technique. The numerical results are presented graphically.

MSC 2010: 35K05, 35R11, 26A33, 44A10, 42A38

Keywords: non-Fourier heat conduction, Caputo fractional derivative, heat absorption, Laplace integral transform, Fourier transform, Mittag-Leffler function

1. Introduction

The classical heat conduction is based on the standard Fourier law and the parabolic heat conduction equation. The time-nonlocal dependence of the heat flux and the temperature gradient with the “long-tail” power kernel [1-4] can be interpreted in terms of fractional integrals and derivatives and results in the time-fractional heat conduction equation

(1)

where T is a temperature, t denotes time, Δ stands for the Laplace operator, a is an analogue of the thermal diffusivity coefficient. The Caputo fractional derivative is defined as [5-7]

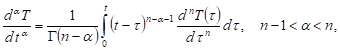(2)

with being the gamma function.

Fractional calculus (the theory of integrals and derivatives of non-integer order) provides the appropriate mathematical tool for description of many phenomena in physics, chemistry, biology, and engineering [8-15].

If volume heat absorption proportional to temperature occurs in a body, then instead of (1) we get

(3)

where the values of the coefficient b > 0 and b < 0 correspond to heat absorption and heat release, respectively. The classical heat conduction equation with the additional term proportional to temperature was considered in [16-18]. Similar equations appear in the theory of bio-heat transfer [19] and in the survival probability [20]. Mathematical and physical aspects of fractional heat conduction equation with heat absorption were studied in the literature in the case of one Cartesian coordinate in [21-24]. In the present paper, we study the fundamental solutions to the Cauchy problem and to the source problem for equation (3) in spherical coordinates in the case of central symmetry. The obtained solutions generalize the results of the paper [25], where the case b = 0 was considered.

2. The fundamental solution to the Cauchy problem

We consider the time-fractional heat conduction equation with one spatial variable in spherical coordinate system

,

(4)

where

Equation (4) is considered under initial conditions

,

(5)

(6)

with being the Dirac delta function. For the sake of convenience and to obtain the nondimensional quantities used in calculations, we have introduced the constant multiplier in equation (5).

The zero condition at infinity is also imposed:

.

(7)

To solve the Cauchy problem under consideration we use the integral transform technique. The Laplace transform with respect to the time is defined as

(8)

with the inverse carried out according to the Fourier-Mellin formula

,

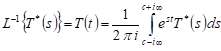(9)

where s denotes the transform variable, is a positive fixed number such that all the singularities of lie to the left of the vertical line .

For the Laplace transform rule, the Caputo fractional derivative requires the knowledge of the initial values of the function and its integer derivatives of the order

(10)

Applying the Laplace transform to equation (4) and taking into account the rule (10) with the initial conditions (5) and (6) gives

. (11)

Next, we use the Fourier transform with respect to the spatial coordinate in the case of spherical symmetry [4, 26]:

,

(12)

.

(13)

.

(14)

Usually the Fourier transform (12)-(13) is used under the assumption of boundedness of T(r) at the origin (see, e.g., [18]); sometimes this assumption is substituted by less restrictive condition prescribing a type of singularity of the function at r = 0 (see, for instance, [27]).

Application of the Fourier transform (12) and formula (14) to equation (11) leads to

.

(15)

Inversion of the integral transforms results in the solution:

(16)

where is the Mittag-Leffler function in one parameter [5-7]

(17)

and the following formula has been used:

.

(18)

Using the nondimensional quantities

(19)

one obtains the following solution:

.

(20)

For the Mittag-Leffler function , and from (20) we get

.

(21)

Taking into account that [28]

(22)

we arrive at the solution

.

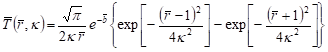(23)

In the particular case , the Mittag-Leffler function can be represented as [4]

,

(24)

and the solution has the following form

.

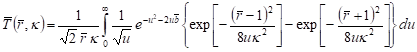(25)

The results of numerical calculations for , different values of and the order of the time-fractional derivative are shown in Figures 1-5.

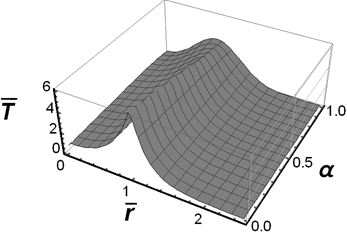Fig. 1. The fundamental solution to the Cauchy problem for and

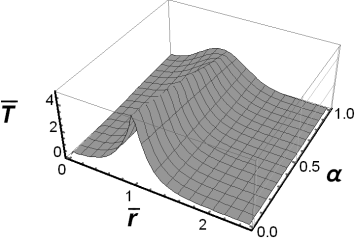
Fig. 2. The fundamental solution to the Cauchy problem for and

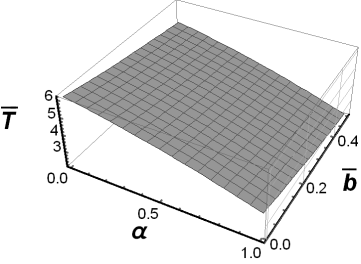
Fig. 3. The fundamental solution to the Cauchy problem for , and

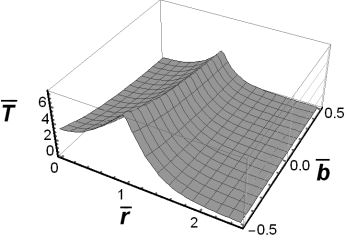
Fig. 4. The fundamental solution to the Cauchy problem for and

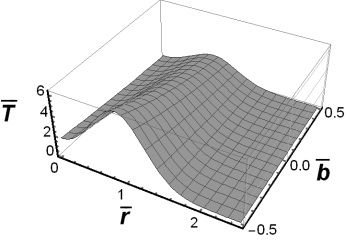
Fig. 5. The fundamental solution to the Cauchy problem for and

3. The fundamental solution to the source problem

Consider the time-fractional heat conduction equation with the source term

(26)

under zero initial conditions

,

(27)

.

(28)

Using the integral transforms technique, we obtain

(29)

As

,

(30)

where is the Mittag-Leffler function in two parameters and [5-7]

(31)

the inverse transforms applied to equation (29) lead to

(32)

and

.

(33)

In this case, the nondimensional temperature is introduced as

(34)

and other nondimensional quantities are the same as in (19).

In the case [4]

.

(35)

Taking into account (35), (38) and (25), we arrive at

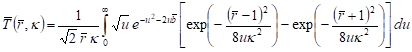. (36)

Figures 6-8 show the results of numerical calculations according to equations (33) and (36) for .

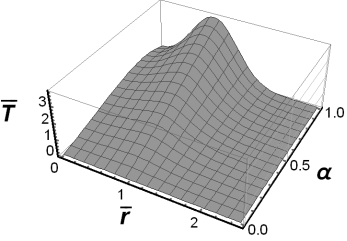
Fig. 6. The fundamental solution to the source problem for and

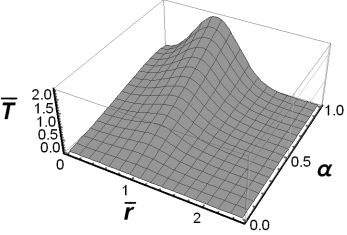
Fig. 7. The fundamental solution to the source problem for and

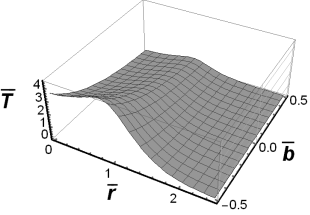
Fig. 8. The fundamental solution to the source problem for and

4. Conclusions

We have solved the time-fractional heat conduction equation with the Caputo fractional derivative in the case of one spatial variable in spherical coordinates. The heat absorption is assumed to be proportional to temperature. The fundamental solutions to the Cauchy problem and to the source problem have been studied. It should be noted that in the case of the classical parabolic heat conduction equation (), the fundamental solutions to the Cauchy problem and to the source problem coincide, whereas for they are different. The results of numerical calculations are displayed in figures for different values of the parameter describing heat absorption and the order of the Caputo fractional derivative. The particular cases of the solutions corresponding to the value coincide with those obtained in [4, 25]. The influence of the sign change of the parameter on temperature is easily observable from the figures. To calculate the Mittag-Leffler functions in (20) and in (33), we have used the algorithms suggested in [29]. It should be emphasized that fractional heat conduction and fractional diffusion have the same origin. At the level of individual particle motions the classical diffusion corresponds to Brownian motion with a mean-squared displacement increasing linearly with time. Anomalous diffusion, which is exemplified by a mean-squared displacement with the power-law time dependence and was observed in different media [13, 30-32], is described by equations with fractional derivatives.

References

[1] Povstenko Y., Fractional heat conduction equation and associated thermal stresses, J. Thermal Stresses 2005, 28, 83-102.

[2] Povstenko Y., Thermoelasticity which uses fractional heat conduction equation, J. Math. Sci. 2009, 162, 296-305.

[3] Povstenko Y., Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder, Fract. Calc. Appl. Anal. 2011, 14, 418-435.

[4] Povstenko Y., Linear Fractional Diffusion-Wave Equation for Scientists and Engineers, Birkhäuser, New York 2015.

[5] Gorenflo R., Mainardi F., Fractional calculus: integral and differential equations of fractional order, [In:] A. Carpinteri, F. Mainardi (eds.), Fractals and Fractional Calculus in Continuum Mechanics, Springer, Wien 1997, 223-276.

[6] Podlubny I., Fractional Differential Equations, Academic Press, San Diego 1999.

[7] Kilbas A., Srivastava H., Trujillo J., Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam 2006.

[8] Hilfer R. (ed.), Applications of Fractional Calculus in Physics, World Scientific, Singapore 2000.

[9] West B.J., Bologna M., Grigolini P., Physics of Fractals Operators, Springer, New York 2003.

[10] Magin R.L., Fractional Calculus in Bioengineering, Begell House Publishers, Connecticut 2006.

[11] Mainardi F., Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models, Imperial College Press, London 2010.

[12] Leszczyński J.S., An Introduction to Fractional Mechanics, The Publishing Office of Częstochowa University of Technology, Częstochowa 2011.

[13] Uchaikin V.V., Fractional Derivatives for Physicists and Engineers, Springer, Berlin 2013.

[14] Atanacković T.M., Pilipović S., Stanković B., Zorica D., Fractional Calculus with Applications in Mechanics, John Wiley & Sons, Hoboken 2014.

[15] Povstenko Y., Fractional Thermoelasticity, Springer, New York 2015.

[16] Crank J., The Mathematics of Diffusion, 2nd ed., Oxford University Press, Oxford 1975.

[17] Carslaw H.S., Jaeger J.C., Conduction of Heat in Solids, 2nd ed., Oxford University Press, Oxford 1959.

[18] Polyanin A.D., Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC, Boca Raton 2002.

[19] Nyborg W.L., Solutions of the bio-heat transfer equation, Phys. Med. Biol. 1988, 33, 785-792.

[20] Abad E., Yuste S.B., Lindenberg K., Survival probability of an immobile target in a sea of evanescent diffusive or subdiffusive traps: a fractional equation approach, Phys. Rev. E 2012, 86, 061120.

[21] Sokolov I.M., Schmidt M.G.W., Sagués F., Reaction-subdiffusion equations, Phys. Rev. E 2006, 73, 031102.

[22] Henry B.I., Langlands T.A.M., Wearne S.L., Anomalous diffusion with linear reaction dynamics: from continuous time random walks to fractional reaction-diffusion equations, Phys. Rev. E 2006, 74, 031116.

[23] Abad E., Yuste S.B., Lindenberg K., Reaction-subdiffusion and reaction-superdiffusion equations for evanescent perticles performing continuous-time random walks, Phys. Rev. E 2010, 81, 031115.

[24] Méndez V., Fedotov S., Horsthemke W., Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities, Springer, Berlin 2010.

[25] Povstenko Y., Fundamental solutions to central symmetric problems for fractional heat conduction equation and associated thermal stresses, J. Thermal Stresses 2008, 31, 127-148.

[26] Sneddon I.N., The Use of Integral Transforms, McGraw-Hill, New York 1972.

[27] Tikhonov A.N., Samarskii A.A., Equations of Mathematical Physics, Dover, New York 1990.

[28] Prudnikov A.P., Brychkov Yu.A., Marichev O.I., Integrals and Series. Vol. 1: Elementary Functions, Gordon and Breach, Amsterdam 1986.

[29] Gorenflo R., Loutchko J., Luchko Yu., Computation of the Mittag-Leffler function and its derivatives, Fract. Calc. Appl. Anal. 2002, 5, 491-518.

[30] Ben-Avraham D., Havlin S., Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, Cambridge 2000.

[31] Metzler R., Klafter J., The random walk’s guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep. 2000, 339, 1-77.

[32] Metzler R., Klafter J., The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, J. Phys. A: Math. Gen. 2004, 37, R161-R208.