Dual-phase lag equation. Stability conditions of a numerical algorithm based on the explicit scheme of the finite difference method
Ewa Majchrzak
,Bohdan Mochnacki
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
DUAL-PHASE LAG EQUATION. STABILITY CONDITIONS OF A NUMERICAL ALGORITHM BASED ON THE EXPLICIT SCHEME OF THE FINITE DIFFERENCE METHOD
Ewa Majchrzak 1, Bohdan Mochnacki 2
1 Silesian University of Technology
Gliwice, Poland
2 University of Occupational Safety
Management in Katowice
Katowice, Poland
ewa.majchrzak@polsl.pl, bmochnacki@wszop.edu.pl
Abstract. The dual-phase lag equation (DPLE) is considered. This equation belongs to the group of hyperbolic PDE, contains a second order time derivative and higher order mixed derivative in both time and space. From the engineer’s point of view, the DPLE results from the generalized form of the Fourier law. It is applied as a mathematical model of thermal processes proceeding in the micro-scale and also in the case of bio-heat transfer problem analysis. At the stage of numerical computations the different approximate methods of the PDE solving can be used. In this paper, the authors present the considerations concerning the stability conditions of the explicit scheme of finite difference method (FDM). The appropriate conditions have been found using the von Neumann analysis. In the final part of the paper, the results of testing computations are shown.
Keywords: heat conduction, dual-phase lag equation, finite difference method, stability conditions of FDM explicit scheme
1. Introduction
Heat conduction processes proceeding in the domain of a solid body can be described by the Fourier-type equation. As is well known, the mathematical form of this equation results from the assumption of the infinite velocity of thermal wave propagation. In the case of micro-scale heat transfer, and also in the case of materials with a specific internal structure (e.g. biological tissue), the Fourier equation should be modified. To take into account the delay effect of the local and temporary heat flux with respect to the temperature gradient, the so-called relaxation time τq is introduced, and then one obtains the Cattaneo-Vernotte equation [1]. If additionally one assumes the non-zero value of the temperature gradient lag time (the thermalization time τT) then the heat conduction is described by the dual-phase lag equation (e.g. [2, 3]) which is a subject of discussion presented in this paper. The considerations concerning the macro-scale heat conduction do not require the inclusion of lag times (for example, in the case of gold τq = 8.5 ps (1 ps = 10–12 s), τT = 90 ps [4]), while the duration of the typical heating/cooling process is measured in seconds, at least. However, considering some of the unusual materials (e.g. soft tissue) the lag times should be taken into account despite the fact that one considers the problem in the macro-scale. For example, the experimental investigation made by Antaki [5] showed that the value of relaxation time is about 2 s for processed meat. Similar problems are discussed in [6].
The primary aim of this publication is to establish the stability conditions for DPLE (in the case when at the stage of numerical modeling the explicit scheme of the FDM is used). In the opinion of the authors, the conditions reported in the literature are either incomplete or contain errors. Often a time step is chosen intuitively (through trial and error). Here the appropriate conditions have been found using the von Neumann analysis [7], the testing computations are also performed.
2. The FDM equation and stability conditions
To simplify the mathematical manipulations the 1D task is analyzed. So, the dual phase lag equation (the hyperbolic PDE) in the form
| (1) |
is considered. Here a is the thermal diffusivity, τq and τT are the relaxation and thermalization times. The equation (1) is supplemented by the appropriate boundary and initial conditions.
The numerical solution of the problem
discussed can be obtained using
the explicit scheme of the FDM. Let us consider the 1D differential mesh being
the Cartesian product ![]() of the geometric
of the geometric ![]() and temporal
and temporal ![]() meshes. Both geometric h and time ∆t
mesh steps are assumed to be the constant values.
meshes. Both geometric h and time ∆t
mesh steps are assumed to be the constant values.
Below, the FDM equation for the internal nodes (i = 1, 2, ..., n−1) will be presented. The successive differential operators are approximated in the following way:
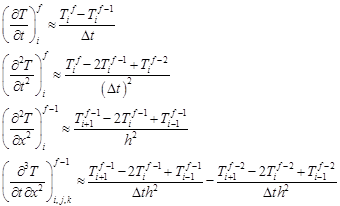 | (2) |
and then
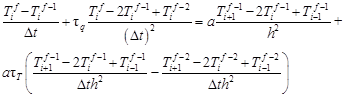 | (3) |
or
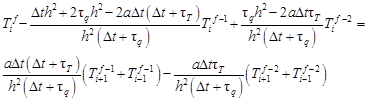 | (4) |
Denoting
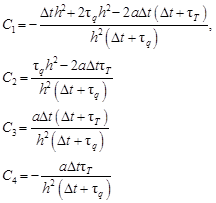 | (5) |
one obtains
| (6) |
The approximation
error carried by ![]() at every node of space i and time f
is
assumed to have a wave form with the wave number denoted by k and the
amplitude by δ [8]:
at every node of space i and time f
is
assumed to have a wave form with the wave number denoted by k and the
amplitude by δ [8]:
| (7) |
As time progresses, to assure convergence, the
amplitude of the approximation
error must be less than unity, i.e. ![]() .
.
Let us introduce the formula (7) into the FDM equation (6)
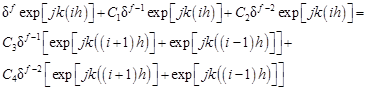 | (8) |
or (after the simplifications)
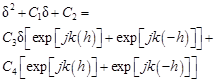 | (9) |
After using the Euler formulas one obtains
| (10) |
Let us denote
| (11) |
and finally
| (12) |
According to [8], the absolute values of the roots of equation (12) will be less than 1 when
| (13) |
So
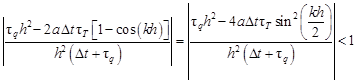 | (14) |
and
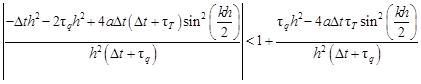 | (15) |
The solution of the first inequality is of the form
| (16) |
For the worst case (from
the viewpoint of stability) one should assume that ![]() and then
and then
| (17) |
In the case of the second inequality, one obtains
| (18) |
Obtaing the solutions of the inequalities (14) and (15) is very tedious, of course, therefore only the final results are presented above. Additionally, one can see that the second condition is more ‘demanding’ and in this situation the inequality (18) determines the value of the critical time step.
3. Results of computations
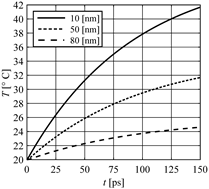
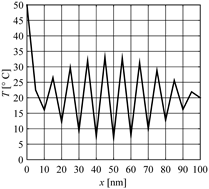
The thin metal film (gold) of thickness 100 nm is considered, The initial temperature Tp = 20°C, the initial heating rate vp = 0. At the moment t = 0 the boundary temperature for x = 0 increased to TB = 50°C, while the temperature for x = G is still equal to Tp (in other words the Dirichlet conditions are assumed). The course of material heating is analyzed. Thermophysical parameters of the film are the following: λ = 315 W/(mK), c = 2.4897 MJ/(m3 K) (this means a = 0.0001265 m/s), τq = 8.5 ps, τT = 90 ps. The mesh step h = 5 nm. The critical time step resulting from inequality (18) is close to ∆tcr = 0.0093 ps. The presented solution in Figure 1 corresponds to ∆t = 0.005 ps and shows the heating curves at the points x = 10, 50, 80 nm. In Figure 2, the unstable solution (temperature profile in the film domain for time t = 1.2 ps) can be observed. The time interval ∆t = 0.01ps is bigger than the critical one and the effect of instability is clearly visible.
|
|
|
|
Fig. 1. Example of stable solution |
Fig. 2. Example of unstable solution |
|
|
|
|
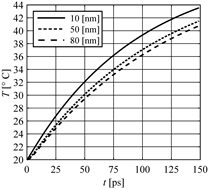
Fig. 3. Stable solution (no-flux condition) |
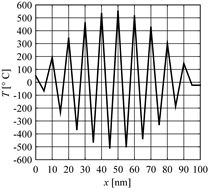
Fig. 4. Unstable solution (no-flux condition) |
The solutions of the similar problem are presented in Figures 3 and 4. In the place of the Dirichlet condition for x = G, the no-flux condition (∂T/∂x = 0) has been taken into account.
5. Conclusions
In the paper the stability conditions for the explicit FDM scheme in the case of the DPL equation are discussed. In particular, the considerations resulting from the von Neumann analysis application are presented. Such an approach leads to two conditions (inequalities), but the fulfillment of the second condition (18) also provides the fulfillment of the first condition (17). It should be also pointed out that the numerical values of the left hand sides of formulas (17) and (18) are very close, but the value of (17) is slightly larger. The condition (18) and its modified form for the case of the control volume method are presented in [9-11]. They have been obtained by transferring a known stability condition for the parabolic equations on the hyperbolic ones (numerical factor C1 - see eq. (5) must be positive). Such an approach has been rather intuitive. The condition (17) was not reported.
The interesting case is shown in Figure 5. The heating curves at the points x = 10, 50, 80 nm have been found for ∆t = 0.009336 ps and this time interval gives a positive value of inequality (17) but a negative one of inequality (18). Despite this fact, the solution obtained is physically correct. This is probably caused from the fact that the critical time step was only minimally exceeded.
Further research will concern the stability conditions for the explicit scheme of the generalized finite difference method [12] (the DPLE will be considered, of course).
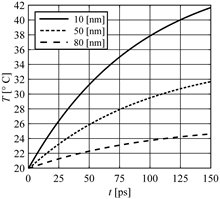
Fig. 5. Solution (temperature profiles) close to the critical time step. The Dirichlet boundary conditions
Acknowledgement
This work is supported by the project No. 2015/19/B/ST8/01101 and sponsored by the National Science Centre (Poland).
References
[1] Cattaneo M.C., A form of heat conduction equation which eliminates the paradox of instantaneous propagation, C.R. Acad. Sci. I - Math. 1958, 247, 431-433.
[2] Tzou D.Y., Macro- to Microscale Heat Transfer: The Lagging Behavior, John Wiley & Sons, Ltd. 2015.
[3] Zhang Z.M., Nano/Microscale Heat Transfer, McGraw-Hill, New York 2007.
[4] Dai W., Nassar R., A domain decomposition method for solving three-dimensional heat transport equations in a double-layered thin film with microscale thickness, Numerical Heat Transfer 2000, Part A, 38, 243-255.
[5] Antaki P.J., New interpretation of non-Fourier heat conduction in processed meat, ASME J. Heat Transfer 2005,127, 189-193.
[6] Roetzel W., Putra N., Das S.K., Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure, Int. J. Therm. Sci. 2003, 42, 541-552.
[7] McDonough J.M., Kunadian I., Kumar R.R., Yang T., An alternative discretization and solution procedure for the dual phase-lag equation, Journal of Computational Physics 2006, 219, 163-171.
[8] Young D.M., Iterative Solution of Large Linear Systems, Academic Press, New York 1971.
[9] Majchrzak E., Mochnacki B., Sensitivity analysis of transient temperature field in microdomains with respect to the dual-phase-lag model parameters, Journal for Multiscale Computational Engineering 2014, 12(1), 65-77.
[10] Mochnacki B., Ciesielski M., Micro-scale heat transfer. Algorithm basing on the Control Volume Method and the identification af relaxation and thermalization times using the search method, Computer Methods in Material Science 2015, 15, 2, 353-361.
[11] Ciesielski M., Mochnacki B., Application of the control volume method using the Voronoi polygons for numerical modeling of bio-heat transfer problems, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 927-935.
[12] Mochnacki B., Majchrzak E., Numerical modeling of casting solidification using generalized finite difference method, THERMEC 2009, PTS 1-4 Book Series: Materials Science Forum 2010, 638-642, 2676-2681.