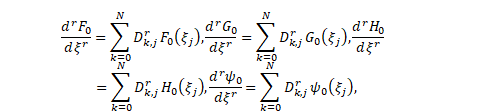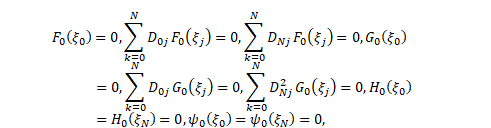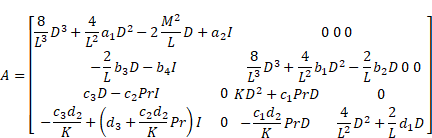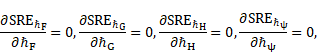Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Chaharborj_2018,
   doi = {10.17512/jamcm.2018.1.02},
   url = {https://doi.org/10.17512/jamcm.2018.1.02},
   year = 2018,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {17},
   number = {1},
   pages = {15--28},
   author = {Sarkhosh S. Chaharborj and  Abbas Moameni},
   title = {Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2018.1.02
UR  - https://doi.org/10.17512/jamcm.2018.1.02
TI  - Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Chaharborj, Sarkhosh S.
AU  - Moameni, Abbas
PY  - 2018
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 15
EP  - 28
IS  - 1
VL  - 17
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Chaharborj, S., & Moameni, A. (2018). Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid. Journal of Applied Mathematics and Computational Mechanics, 17(1), 15-28. doi:10.17512/jamcm.2018.1.02

Chaharborj, S. & Moameni, A., 2018. Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid. Journal of Applied Mathematics and Computational Mechanics, 17(1), pp.15-28. Available at: https://doi.org/10.17512/jamcm.2018.1.02

[1]S. Chaharborj and A. Moameni, "Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 1, pp. 15-28, 2018.

Chaharborj, Sarkhosh S., and Abbas Moameni. "Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid." Journal of Applied Mathematics and Computational Mechanics 17.1 (2018): 15-28. CrossRef. Web.

1. Chaharborj S, Moameni A. Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(1):15-28. Available from: https://doi.org/10.17512/jamcm.2018.1.02

Chaharborj, Sarkhosh S., and Abbas Moameni. "Spectral-homotopy analysis of MHD non-orthogonal stagnation point flow of a nanofluid." Journal of Applied Mathematics and Computational Mechanics 17, no. 1 (2018): 15-28. doi:10.17512/jamcm.2018.1.02

SPECTRAL-HOMOTOPY ANALYSIS OF MHD NON-ORTHOGONAL STAGNATION POINT FLOW OF A NANOFLUID

Sarkhosh S. Chaharborj ^1,2, Abbas Moameni ¹

¹ School of Mathematics and Statistics, Carleton University, Ottawa,
K1S 5B6, Canada
² Department of Mathematics, Islamic Azad University, Bushehr
Branch, Bushehr, Iran
saman.seddighi@carleton.ca, momeni@math.carleton.ca

Received: 14 May 2017; Accepted: 24 January 2018

Abstract. In this article, we investigate the theoretical study of the magnetohy-drodynamic (MHD) non-orthogonal stagnation point flow of a nanofluid towards a stretching. The partial differential equations that model the problem are reduced to ordinary differential equations which are then solved analytically using the improved Spectral Homotopy Analysis Method (SHAM). Com­parisons of our results from SHAM and numerical solutions show that this method is a capable tool for solving this type of linear and nonlinear problems semi-analytically.

MSC 2010: 34B15, 34K07, 34K28

Keywords: nanofluid, MHD stagnation flow, stretching sheet, SHAM

1. Introduction

The boundary layer flow problems have various applications in the fluid mechanics. Namely, the classical two-point nonlinear boundary value Blasius problem which models viscous fluid flow over a semi-infinite flat plate, nonlinear Falkner-Skan equation and magnetohydro dynamic (MHD) boundary layer flow.

Most researchers have used the semi-analytical and numerical methods such as the Runge-Kutta methods [1], finite difference methods [2], finite element methods [3] and spectral methods [4] to solve this type of equations. In recent years, for solving nonlinear differential equations, several analytical and semi-analytical methods have been established such as the variational iteration method [5, 6], Adomian decomposition method [7], differential transform method [8], homotopy analysis method (HAM) [9-13], and the spectral-homotopy analysis (SHAM) [14, 15] and more recently, the successive linearization method [16, 17].

All analytical and semi-analytical methods mostly focus on the single and independent linear and nonlinear equations of the boundary layer flow problems. In this paper, we present an improved spectral-homotopy analysis method to solve the system of boundary layer problems. The considered system contains the nonlinear boundary differential equations governed from partial differential equations of magnetohydrodynamic (MHD) non-orthogonal stagnation point flow of a nanofluid towards a stretching.

2. Formulation of the problem

We investigate the steady two-dimensional stagnation point flow of a second grade nanofluid over a stretching surface [18, 19]. Two equal and opposite forces are applied along the z-axis so that the surface is stretched keeping the origin fixed, as shown in Figure 1. We further assume that the surface has temperature and the fluid has uniform ambient temperature (here ). The flow is subjected to the combined effect of thermal radiation and a transverse magnetic field of strength , which is assumed to be applied in the positive direction, normal to the surface. The induced magnetic field is also assumed negligible compared to the applied magnetic field, so it can be neglected. It is further assumed that the base fluid and the suspended nanoparticles are in thermal equilibrium. It is chosen that the coordinate system -axis is along the stretching sheet and -axis is normal to the sheet. Under the above assumptions, the governing equation of the conservation of mass, momentum, energy and nanoparticles fraction in the presence of a magnetic field and thermal radiation past a stretching sheet can be expressed as,

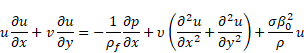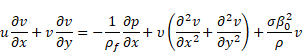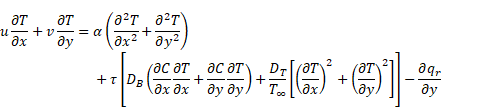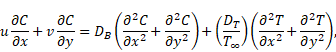on .

Here and are the velocity components in the x and y directions. and k are the local temperature of the fluid, nano-particle fraction, kinematic viscosity, density, electrical conductivity, and permeability of the saturated porous medium parameters, respectively. is the thermal diffusivity, is the Brownian motion coefficient, in general the thermal diffusion coefficient is a function of temperature and concentration, which complicates the description of thermophoresis and is the ratio of effective heat capacity of the nanoparticle material to heat capacity of the fluid and is the density of nano- fluid at constant pressure. The boundary conditions are,

at as

(1)

Where and , are positive constants with the dimension of (time)^–1 indicating potential flow and linear shear flow parallel to the streamwise direction (shear stress ) contributions into the oblique flow, respectively. Radiative heat flux in governing boundary layer equation of energy is approximated by Rosseland approximation, which gives,

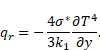It is assumed that the temperature difference within the flow is so small that can be expressed as a linear function of . This can be obtained by expanding in a Taylor series about and neglecting the higher order terms will results . Heat is transferred by forced convection, which involves the only normal component of flow field. Introducing the following dimensionless quantities, the mathematical analysis of the problem is simplified by using similarity transformations.

According to the presented similarity transformations as shown in [18, 19], the above systems can be converted to the following ordinary differential equations along with the corresponding boundary conditions,

,

(2)

,

(3)

(4)

(5)

on and subject to the boundary conditions,

(6)

as ,

(7)

where, and are positive constants and is striking angle, is the magnetic number, is the Prandtl number, is thermal radiation effect, is the thermophoresis parameter, is the Lewis number.

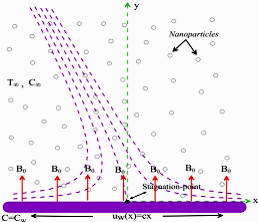
Fig. 1. Geometry of problem

3. The spectral homotopy analysis method

At the beginning, for transferring the domain of the problem from to , the domain truncation method has been utilized. The computational domain where is a fixed length can be used to approximate the domain . Here, is taken to be larger than the thickness of the boundary layer [15]. The simple algebraic mapping for transferring the interval to the Chebyshev domain is as follows,

(8)

For convenience, the boundary conditions have been made homogeneous by applying the trans­formations as,

(9)

where, , , and are chosen so as to satisfy the boundary conditions (6) and (7) as,

(10)

Substituting Eqs. (10) into Eqs. (2)-(7) yields that,

	(11)
	(12)
	(13)
	(14)

with the boundary conditions,

(15)

where the coefficients in Eq. (11) are defined by, and the coefficients in Eq. (12) appear as following:

and here are the coefficients and in Eqs. (13) and (14) respectively,

By solving the linear parts of Eqs. (2) up to (5), we can obtain the initial solutions,

	(16)
	(17)

(18)

(19)

subject to the boundary conditions,

(20)

The Chebyshev pseudo-spectral method has been used to solve Eqs. (16) up to (19). The unknown functions and are aproximated as truncated series of Chebyshev polynomials as follows,

(21)

where and are the Chebyshev polynomials with coefficients , and respectively; , are Gauss-Lobatto collocation points defined as,

Derivatives of the functions , , and at the collocations points are defined as,

(22)

where is the order of differentiation and is the Chebyshev spectral differential matrix with the entries as,

with is defined as follows,

substituting Eqs. (21) into Eqs. (16)-(19) yields, subject to the boundary conditions,

(23)

where,

(24)

The superscript T denotes the transpose, “diag” is a diagonal matrix and I is an identity matrix of size . The values of are obtained from the equation, which is the initial approximation for the solution of Eqs. (11)-(14) by the SHPM. The 0-th order deformation equations are given by,

with,

.

here H is the nonzero convergence controlling auxiliary parameter; L and N are linear and nonlinear operators, respectively, defined as,

The -th order deformation equations are given by,

(25)

subject to the boundary conditions,

, ,

(26)

where:

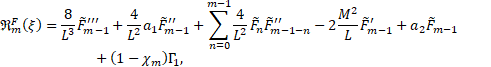
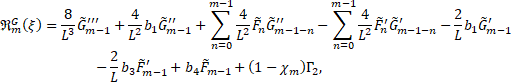
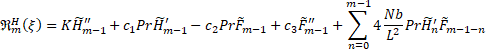
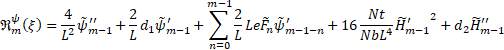
(27)

Applying the Chebyshev pseudospectral transformation to Eqs. (25)-(27) gives,

(28)

subject to the boundary conditions:

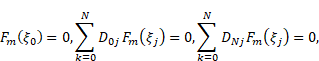
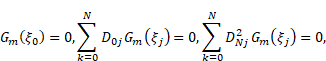
(29)

where are defined in Eq. (24) and

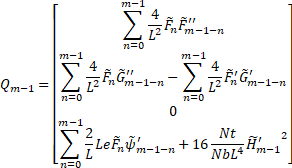
Boundary conditions (29) are implemented in matrix A on the left side of (28) in rows , , , and , respectively. Matrix in the right-hand side of Eq. (28), and have corresponding rows and all columns equal to zero. This recursive formula when , can be written as follows,

.

(30)

Therefore, the higher-order approximation for has been obtained by starting from the initial approximation.

4. Optimization of convergence-control parameters based on the square residual errors

From Eqs. (27), error functions can be defined as follows:

(31)

In what follows, we are going to find the optimal values of , , and , by using the convergence-control for various values of order will find. The square residual error (SRE) method can help us to optimize the convergence-control parameters as follows:

(32)

(33)

where , , and are the th-order SHAM approximations of the functions , , and , respectively. Obviously, when then we will have , , and that correspond to convergent series solutions of SHAM. The points at which the gradient of square residual error functions presented in Eqs. (32) and (33) with respect to convergence-control parameters vanish, are precisely the optimal values of , , and for th-order SHAM approximation as follows:

(34)

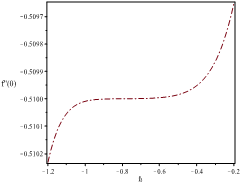
Figure 2 presents the optimal values and the optimal square residual errors in the at different values of . This figure shows that the optimal values of is approximately between –1 and –0.4. By choosing from this optimal interval, the results obtained from SHAM will have good accuracy. Table 1 presents the optimal values of , , and and optimal values of the square residual error at a different order of in the . Table 1 is showing that with increasing the order of approximation , the square residual error will decrease. To obtain the results of Table 1, Matlab R2015b software has been used.

5. Results and discussion

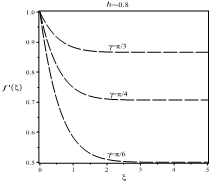
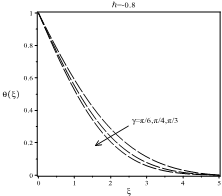
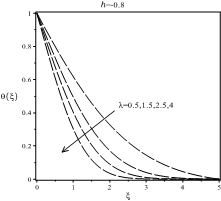
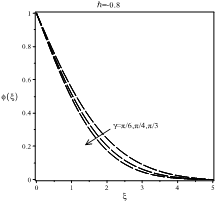
Figures 3, 5 and 7 present the influence of on and, temperature and concen­- tration profiles when and . As shown, by decreasing the values of appeared in the initial conditions and from to the profile is decreasing and both temperature and concentration profiles and are increasing. The results indicate that the curves reduce with a negative slope for . Figure 3 is showing that with decreasing the striking angle at a fixed value of , heat transfer velocity will decrease. Figure 5 indicates that with decreasing the striking angle at a fixed value of , temperature will increase. Figure 7 is showing that with decreasing the striking angle at a fixed value of , heat transfer concentration will increase.

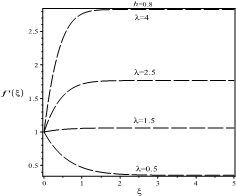
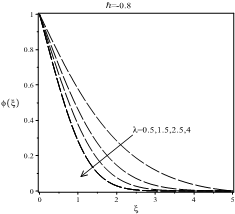
Figures 4, 6 and 8 are showing the influence of on and, temperature and concentration profiles when and . Note that, by increasing the values of appeared in the initial condition form 0.5 to 4 the profile is increasing and both temperature and concentration profiles and are decreasing. Figures 4 indicate, however, that they have positive slopes for , and the curves reduce with a negative slope for . Figure 4 is showing that with increasing the velocity parameter at a fixed value of , heat transfer velocity will increase. Figure 6 indicates that with increasing the velocity parameter at a fixed value of , temperature will increase. Figure 8 is showing that with increasing the velocity parameter at a fixed value of , heat transfer concentration will increase.

In order to test the accuracy of the present results, we have compared the results for skin friction coefficient with those reported by Lok et al. [20]. This comparison is presented in Table 2. It is noticed that this comparison shows an excellent agreement, so that we are confident that the present results are accurate. Table 2 shows a comparison of the re­sults for for at different values of and . Results of this table indicate that with increasing parameter from 0.2 to 3.0, for any values of parameter , is increasing. As seen, by increasing from to , the function is increasing with a high speed. To obtain the results of Table 2, Matlab R2015b software has been used.

Table 2

Comparison of the results for for at different values of and . With and

Conclusion

We have investigated the modified spectral homotopy analysis method (SHAM) for solving a complicated nonlinear dynamical system in the MHD non-orthogonal stagnation point flow of a nanofluid towards a stretching. Numerical results show the effectiveness of our proposed method for solving complicated linear and non-linear dynamical systems in the heat transfer and heat flow problems. The results indicate that they have positive slopes for , and the curves reduce with a negative slope for . The optimal interval for is between –1 and –0.4. The results for skin friction coefficient from our presented method with and have been compared with those reported by Lok et al. at references [20]. This comparison shows an excellent agreement, so that we are confident that the present results are accurate.

References

[1] Chaharborj, S.S., Kiai, S.S., Bakar, M.A., Ziaeian, I., & Fudziah, I. (2012). New impulsional potential for a paul ion trap. International Journal of Mass Spectrometry, 309, 63-69.

[2] Nayak, I., Nayak, A.K., & Padhy, S. (2016). Implicit fnite difference solution for the magneto- hydro-dynamic unsteady free convective flow and heat transfer of a third-grade fluid past a porous vertical plate. Inter­national Journal of Mathematical Modelling and Numerical Optimisation, 7(1), 4-19.

[3] John, V. (2016). Finite Element Methods for Incompressible Flow Problems. Berlin: Erscheint demnchst bei Springer.

[4] Chen, S., & Wang, Y. (2016). A rational spectral collocation method for third-order singularly perturbed prob­lems. Journal of Computational and Applied Mathematics, 307, 93-105.

[5] Moameni, A. (2011). Non-convex self-dual lagrangians: New variational principles of symmetric boundary value problems. Journal of Functional Analysis, 260(9), 2674-2715.

[6] Wazwaz, A.M. (2016). Solving systems of fourth-order emden-fowler type equations by the variational iteration method. Chemical Engineering Communications, 203(8), 1081-1092.

[7] Hosseini, S., Babolian, E., & Abbasbandy, S. (2016). A new algorithm for solving van der pol equation based on piecewise spectral adomian decomposition method. International Journal of Industrial Mathematics, 8(3), 177-184.

[8] Fidanoglu, M., Komurgoz, G., & Ozkol, I. (2016). Heat transfer analysis of fins with spine geometry using differential transform method. International Journal of Mechanical Engineering and Robotics Research, 5(1), 67-71.

[9] Shahlaei-Far, S., Nabarrete, A., & Balthazar, J.M. (2016). Homotopy analysis of a forced nonlinear beam model with quadratic and cubic nonlinearities. Journal of Theoretical and Applied Mechanics, 54(4), 1219-1230.

[10] Semary, M.S., & Hassan, H.N. (2016). The homotopy analysis method for q-difference equations. Ain Shams Engineering Journal, DOI http://dx.doi.Org/10.1016/j.asej.2016.02.005.

[11] Hayat, T., Mumtaz, M., Shafiq, A., & Alsaedi, A. (2017). Stratified magnetohydrodynamic flow of tangent hyperbolic nanofluid induced by inclined sheet. Applied Mathematics and Mechanics, 38(2), 271-288.

[12] Zhu, J., Wang, S., Zheng, L., & Zhang, X. (2017). Heat transfer of nanofluids considering nanoparticle migration and second-order slip velocity. Applied Mathematics and Mechanics, 38(1), 125-136.

[13] Zhao, Q., Xu, H., Tao, L., Raees, A., & Sun, Q. (2016). Three-dimensional free bio-convection of nanofluid near stagnation point on general curved isothermal surface. Applied Mathematics and Mechanics, 37(4), 417-432

[14] Motsa, S.S., Marewo, G.T., Sibanda, P., & Shateyi, S. (2011). An improved spectral homotopy analysis method for solving boundary layer problems. Boundary Value Problems, 2011(1), 3-11.

[15] Rashidi, M.M., Rostami, B., Freidoonimehr, N., & Abbasbandy, S. (2014). Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects. Ain Shams Engineering Journal, 5(3), 901-912.

[16] Bhatti, M.M., Shahid, A., & Rashidi, M.M. (2016). Numerical simulation of fluid flow over a shrinking porous sheet by Successive linearization method. Alexandria Engineering Journal, 55(1), 51-56.

[17] Ahmed, M.A.M., Mohammed, M.E., & Khidir, A.A. (2015). On linearization method to MHD boundary layer convective heat transfer with low pressure gradient. Propulsion and Power Research, 4(2), 105-113.

[18] Rashidi, M.M., Abelman, S., & Mehr, N.F. (2013). Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. International Journal of Heat and Mass Transfer, 62, 515-525.

[19] Rashidi, M.M., Ali, M., Freidoonimehr, N., & Nazari, F. (2013). Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm. Energy, 55, 497-510.

[20] Lok, Y.Y., Amin, N., & Pop, I. (2006). Non-orthogonal stagnation point flow towards a stretching sheet. International Journal of Non-Linear Mechanics, 41(4), 622-627.