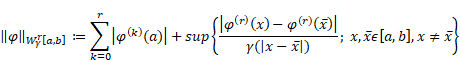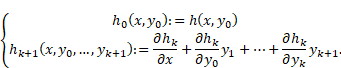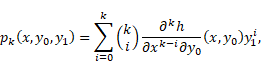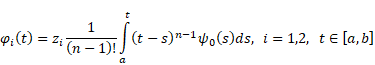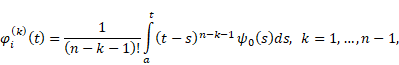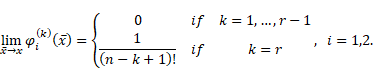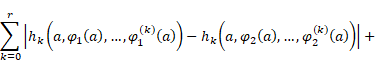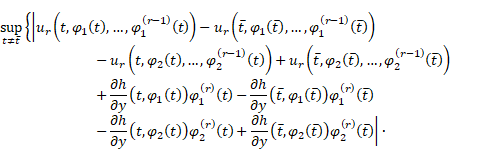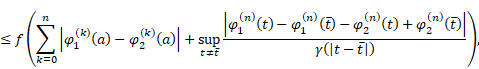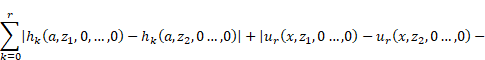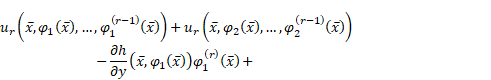Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Lupa_2017,
   doi = {10.17512/jamcm.2017.4.04},
   url = {https://doi.org/10.17512/jamcm.2017.4.04},
   year = 2017,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {16},
   number = {4},
   pages = {37--45},
   author = {Maria Lupa and  Małgorzata Wróbel},
   title = {Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2017.4.04
UR  - https://doi.org/10.17512/jamcm.2017.4.04
TI  - Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Lupa, Maria
AU  - Wróbel, Małgorzata
PY  - 2017
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 37
EP  - 45
IS  - 4
VL  - 16
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Lupa, M., & Wróbel, M. (2017). Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics, 16(4), 37-45. doi:10.17512/jamcm.2017.4.04

Lupa, M. & Wróbel, M., 2017. Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics, 16(4), pp.37-45. Available at: https://doi.org/10.17512/jamcm.2017.4.04

[1]M. Lupa and M. Wróbel, "Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 4, pp. 37-45, 2017.

Lupa, Maria, and Małgorzata Wróbel. "Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions." Journal of Applied Mathematics and Computational Mechanics 16.4 (2017): 37-45. CrossRef. Web.

1. Lupa M, Wróbel M. Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(4):37-45. Available from: https://doi.org/10.17512/jamcm.2017.4.04

Lupa, Maria, and Małgorzata Wróbel. "Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions." Journal of Applied Mathematics and Computational Mechanics 16, no. 4 (2017): 37-45. doi:10.17512/jamcm.2017.4.04

UNIFORMLY BOUNDED NEMYTSKIJ OPERATORS ACTING BETWEEN THE BANACH SPACES OF GENERALIZED HÖLDER FUNCTIONS

Maria Lupa, Małgorzata Wróbel

Institute of Mathematics, Czestochowa University of Technology
Czestochowa, Poland
maria.lupa@im.pcz.pl, malgorzata.wrobel@im.pcz.pl

Received: 23 October 2017; Accepted: 13 November 2017

Abstract. We investigate the Nemytskij (composition, superposition) operators acting between Banach spaces of -times differentiable functions defined on the closed intervals of the real line with the -derivatives satisfying a generalized Hölder condition. The main result says that if such a Nemytskij operator is uniformly bounded (in a special case uniformly continuous) then its generator is an affine function with respect to the second variable, i.e., the Matkowski representation holds. This extends an earlier result where an operator is assumed to be Lipschitzian.

MSC 2010: 47H30, 26A11

Keywords: Nemytskij (composition, superposition) operator, generalized Hölder condition, uniformly bounded mapping, uniformly continuous mapping

1. Introduction

The Nemytskij operators occur frequently in the theory of integral equations, differential equations, variational calculus or in optimization theory. There is vast literature devoted to applications of the results connected with the theory of the composition operators (see, for instance [1], where such operators occur in the problems of option pricing within the Black-Scholes model for time-dependent volatility).

Let be an interval of the real line () and let denote the set of all functions For a given function , the mapping defined by

,

is called a composition (Nemytskij or superposition) operator of a generator.

In 1982 J. Matkowski [2] proved that if H maps a Banach space of Lipschitzian functions with the classical -norm into itself and is globally Lipschitzian, i.e., if for some constant ,

then

(1)

for some functions i.e., h is an affine function with respect to the second variable. Analogous results for representations of the generators of globally Lipschitzian operators have been proved for some other function spaces [3-7]. Later, it was observed that these results remain true if the Lipschitz norm-continuity of H is replaced by its uniform continuity [8, 9].

In 2011, J. Matkowski [10] proved, under very general assumptions, that for the function spaces including the Hölder spaces as a special case, the uniform continuity of the operator H can be replaced by a much weaker condition of the uniform boundedness (which is weaker than norm-boundedness), see also [11, 12].

The purpose of this paper is to show that if maps the space of -times differentiable functions with the -derivative satisfying a generalized Hölder condition into , where and is uniformly bounded, then the Matkowski representation holds, i.e., the generator of must be of the form (1) for some . This extends the main result of [5, 6] where is assumed to be Lipschitzian.

2. Preliminaries

Given a closed interval ( put . Let following condition:

(Γ) is increasing and concave, γ(0) = 0, ,

Given , denote by the set of all r-times differentiable functions such that their r-th derivatives satisfy the following condition (so called the generalized Hölder condition or the -Hölder condition): there exists a constant such that

(2)

where satisfy condition (Γ).

It is known that the space endowed with the norm

(3)

is a Banach space [3, 4].

Let , stand for the class of all r-times differentiable functions , whose r-th derivatives satisfy the Lipschitz condition on .

Remark 2.1. Observe, that if with the constant , then fulfils (2) with the constant .

Indeed, by , we get the monotonicity of the function

and, consequently, we have

for all

Remark 2.2 ([6], Remark 1). If and is finite, denotes the right derivative of γ at then

Remark 2.3. Let us notice that the function defined by , where , , fulfils the assumption and .

Definition 2.1. Let and a function be fixed. The mapping given by

,

is said to be a composition (Nemytskij or superposition) operator. The function h is referred to as the generator of the operator H.

Assume now, that the function h fulfils the following condition:

(i) is -times differentiable in , , and all its r-th order partial derivatives fulfill the generalized Hölder conditions with respect to the first variable and Lipschitz condition with respect to the second variable.

Define, by recurrence, functions as follows:

(4)

Before formulating the main results of our paper, we will need the following two lemmas.

Lemma 2.1 ([6], Lemma 1). If the assumption (i) is fulfilled, then the functions , defined by (4), are -times continuously differentiable in and, for , we have

where

(5)

and is a polynomial of the variables whose coefficients are functions of the variables and are of the class with respect to and .

Lemma 2.2 ([6], Lemma 2). If the assumption (i) is fulfilled, and

=, ,

then the derivatives of fulfil the following system of equations:

,

and

3. Main results

Theorem 3.1. Let be fixed and let a function be such that for any the function is r-times differentiable and its r-th derivatives satisfy the Lipschitz condition on If the composition operator H of the generator h maps the space into and satisfies the inequality

(6)

for some function then there exist and such that

Proof. For every fixed the function , , as a constant, is -times differentiable and its n-th derivatives satisfy the generalized Hölder condition, so, by assumption, Thus, taking into account the assumption, it follows that the function h fulfils (i).

Let us fix and define the function

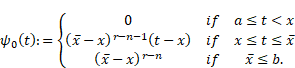It is obvious that with the constant , so, by Remark 1, satisfy the generalized Hölder condition with the constant

Let us take arbitrary , . Putting

(7)

we get

(8)

and

(9)

for all

Hence, , , and, by the definition of the function , for all , we obtain

, ,

(10)

and

, ,

(11)

Since, by (8),

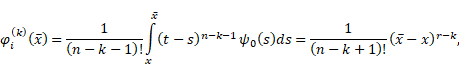
and, by (9),

therefore

(12)

Setting , where are defined in Lemma 1, inequality (6) has the following form

for all

Omitting the sign supremum on the left hand side of the above inequality and putting , by (10), (11), we get

and, consequently,

Hence, letting in so obtained inequality, by the right-hand side continuity in zero of and (12), we have

whence,

Thus is linear with respect to the second variable and, consequently, there exist functions such that

(13)

Since for all (13),

therefore , which completes the proof.

In the sequel the following definition plays a crucial role:

Definition 3.1 ([10], Definition 1). Let and be two metric spaces. We say that a mapping is uniformly bounded if, for any, there exists a real number such that for any nonempty set , we have

.

The main result of this paper reads as follows:

Theorem 3.2. Let be fixed and let a function be such that for any the function is r-times differentiable and its r-th derivatives satisfy the Lipschitz condition on If the composition operator of the generator maps the space into and is uniformly bounded, then there exist and such that

and

, (

Proof. Take any and arbitrary such that

.

Since by the uniform boundedness of , we have,

that is

and the result follows from Theorem 1.

Remark 3.1. If the function in Definition 3.1 is right continuous at and (or if only ), then, clearly, the uniform boundedness of the involved operator reduces to its uniform continuity.

Remark 3.2. Taking in Theorem 3.2 such that is finite, , for some constant , we get the main result of Knop [5].

Remark 3.3. Theorem 3.2 also extends the result of Lupa [6], where is such that (0) , ( and .

4. Conclusions

We show that if a Nemytskij composition operator mapping the space of -times differentiable functions with the -th derivative satisfying a generalized Hölder condition into is uniformly bounded or uniformly continuous, then its generator is an affine function with respect to the second variable. This significantly extends the result of [5, 6] where much stronger Lipschitz norm continuity of is assumed.

References

[1] Krämer R., Mathé P., Modulus of continuity of Nemytskii operators with application to the problem of option pricing, Journal of Inverse and Ill-posed Problems 2008, 16(5), 435-461.

[2] Matkowski J., Functional equation and Nemytskij operators, Funkcial Ekv. 1982, 25, 127-132.

[3] Appell J., Banaś J., Merentes N., Bounded Variation and Around, De Gruyter Studies in Non- linear Analysis and Applications, Volume 17, Würzburg 2014.

[4] Appell J., Zabrejko P.P., Nonlinear Superposition Operators, Cambridge University Press, Cambridge-New York-Port Chester-Melbourne-Sydney 1990.

[5] Knop J., On globally Lipschitzian Nemytskii operator in a special Banach space of functions, Fasciculi Mathematici 1990, 280(21), 79-85.

[6] Lupa M., Form of Lipschitzian operator of substitution in some class of functions, Zeszyty Naukowe Politechniki Łódzkiej 1990, Matematyka, 21, 87-96.

[7] Matkowski J., Miś J., On a characterization of Lipschitzian operators of substitution in the space BV[a,b], Math. Nachr. 1984, 117, 155-159.

[8] Matkowski J., Uniformly continuous superposition operators in the space of Hölder functions, J. Math. Anal. App. 2009, 359, 56-61.

[9] Matkowski J., Uniformly continuous superposition operators in the spaces of bounded variation functions, Math. Nach. 2010, 283(7), 1060-1064.

[10] Matkowski J., Uniformly bounded composition operators between general Lipschitz functions normed spaces, Topol. Methods Nonlinear Anal. 2011, 38(2), 395-406.

[11] Matkowski J., Wróbel M., Uniformly bounded set-valued Nemytskij operators acting between generalized Hölder function spaces, Cent. Eur. J. Math. 2012, 10(2), 609-618.

[12] Wróbel M., Uniformly bounded Nemytskij operators between the Banach spaces of functions of bounded n-th variation, J. Math. Anal. Appl. 2012, 391, 451-456.