(D,O)-species of bounded representation type

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Gubareni_2016,
   doi = {10.17512/jamcm.2016.4.05},
   url = {https://doi.org/10.17512/jamcm.2016.4.05},
   year = 2016,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {15},
   number = {4},
   pages = {39--50},
   author = {Nadiya Gubareni},
   title = {(D,O)-species of bounded representation type},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2016.4.05
UR  - https://doi.org/10.17512/jamcm.2016.4.05
TI  - (D,O)-species of bounded representation type
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Gubareni, Nadiya
PY  - 2016
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 39
EP  - 50
IS  - 4
VL  - 15
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Gubareni, N. (2016). (D,O)-species of bounded representation type. Journal of Applied Mathematics and Computational Mechanics, 15(4), 39-50. doi:10.17512/jamcm.2016.4.05

Gubareni, N., 2016. (D,O)-species of bounded representation type. Journal of Applied Mathematics and Computational Mechanics, 15(4), pp.39-50. Available at: https://doi.org/10.17512/jamcm.2016.4.05

[1]N. Gubareni, "(D,O)-species of bounded representation type," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 4, pp. 39-50, 2016.

Gubareni, Nadiya. "(D,O)-species of bounded representation type." Journal of Applied Mathematics and Computational Mechanics 15.4 (2016): 39-50. CrossRef. Web.

1. Gubareni N. (D,O)-species of bounded representation type. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(4):39-50. Available from: https://doi.org/10.17512/jamcm.2016.4.05

Gubareni, Nadiya. "(D,O)-species of bounded representation type." Journal of Applied Mathematics and Computational Mechanics 15, no. 4 (2016): 39-50. doi:10.17512/jamcm.2016.4.05

(D,O)-SPECIES OF BOUNDED REPRESENTATION TYPE

Nadiya Gubareni

Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
nadiya.gubareni@yahoo.com
Received: 11 April 2016; accepted: 29 May 2016

Abstract. We describe weak (D,O)-species of bounded representation type in terms of Dynkin diagrams and diagrams with weights. We reduce the problem of their description to flat mixed matrix problems over discrete valuation rings and their common skew field of fractions.

Keywords: species, (D,O)-species, flat mixed matrix problems, discrete valuation ring, Dynkin diagrams

1. Introduction

The representations of species which are first introduced by P. Gabriel [1] are closely connected with representations of finitely dimensional algebras and Artinian rings and were studied by many authors (see e.g. [1-3]). This paper is devoted to the study of (D,O)-species which can be considered as a type of a generalization of these species. They play an important role in the representation theory of some classes of rings, for example, of right hereditary SPSD-rings. We use the main definitions and results from the previous paper [4].

Let W = (F_i, _iM_j)_{i,j Î I} be a weak (D,O)-species, where all F_i are equal to O_i or D, and _iM_j is a (D, D)-bimodule that is finite dimensional both as a right and left D-vector space (see [1]). Let I = {1,2, …, n}. The diagram of W is a directed graph Q(W) whose vertices are indexed by the numbers 1, 2, ..., n, and the number of arrows from a vertex i to a vertex j is

A vertex i of the graph Q(W) is said to be marked if F_i = O_i and we say that F_i is a weight of this vertex. A marked vertex is denoted by . By definition of a weak (D,O)-species, each marked vertex is minimal in Q(W). The graph obtained from the graph Q(W) with marked vertices by deleting the orientation of all arrows that connect the unmarked vertices of Q(W) will be called the diagram with weights of a (D,O)-species W. Recall that a (D,O)-species is of bounded representation type if the dimensions of its indecomposable finite dimensional representations have an upper bound.

In this paper we prove the following theorem, which describes the structure of (D,O)-species of bounded representation type in terms of Dynkin diagrams and diagrams with weights. The proof of this theorem is reduced to solving some flat mixed matrix problems over discrete valuation rings and their common skew field of fractions as it was developed in [4].

Theorem 1. Let {O_i}_iÎI be a family of discrete valuation rings with a common skew field of fractions D. A weak (D,O)-species is of bounded representation type if and only if its diagram Q(W) is a finite disjoint union of Dynkin diagrams of the form A_n, D_n, E₆, E₇, E₈ and the following diagrams with weights:

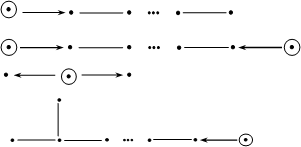
Throughout this paper all rings are assumed to be associative with identity.

2. Proof of the necessity in Theorem 1

Lemma 2.1. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4}. Then a (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(2.2)

is of unbounded representation type.

Proof. We prove this lemma for the case F₁ = O, F₂ = F₃ = F₄ = D, ₁M₂ = ₁M₃ = ₁M₄ = = _OD_D and _iM_j = 0 for other i,j Î I. Write J = {1,2,3}.

Let X be a right O-module, Y_i a right D-vector space, and let be a D-linear mapping for i Î J.

Consider the category Rep(W) whose objects are representations M = (X, Y_i, j_i,)_iÎJ, and a morphism from an object M to an object M¢ = (X¢, Y¢_i, j¢_i,)_{i ÎJ} is a set of homomorphisms (a, b_i) _{i Î J}, in which a: X ® X¢ is a homomorphism of O-modules, b_i: Y_i ® Y¢_i is a homomorphism of D-vector spaces (iÎ J), and the following equalities hold:

(2.3)

Let us show that the category Rep(W) is of unbounded representation type. Let X be a finitely generated free O-module with basis w₁, ... , w_n; and let Y_i be a finite dimensional D-space with basis (i = 1,2,3). Suppose

(iÎ J) (2.4)

where for i Î J, s = 1, ..., n. Then the matrices , iÎ J, define the representation M uniquely up to equivalence.

Let UÎM_n(O) be the matrix corresponding to the isomorphism a, and let be the matrices corresponding to the isomorphisms b_i, i Î J. If are the matrices corresponding to a representation M¢, then equalities (2.3) have the following matrix form:

.

(2.5)

We obtain the following matrix problem:

Given a block-rectangular matrix T = with the following admissible transformations:

1. Right O-elementary transformations of columns of T.

2. Left D-elementary transformations of rows within each block A_i (i = 1,2,3).

Set

,

, ,

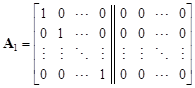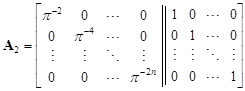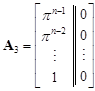where p Î R = rad O, p ¹ 0. By [5, Lemma 4], the matrix T is indecomposable and therefore the species with diagram (2.2) is of unbounded representation type.

Lemma 2.6. Let O be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4}. Then a (D,O)-spe-cies W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(2.7)

is of unbounded representation type.

Proof. Analogously as in the proof of Lemma 2.1, we obtain the following matrix problem:

Given a block-triangular matrix T = . The following transformations are admitted:

1. Right O-elementary transformations of columns within the first vertical strip of the matrix T.

2. Right D-elementary transformations of columns within the second vertical strip of the matrix T.

3. Left D-elementary transformations of rows within each horizontal strip of the matrix T.

Reduce A₃ to the form and obtain A₂ of the form . It is possible to add any row of the matrix B₂ multiplied on the left by elements of D to any column of the matrix B₁. Thus the matrices A₁, B₁ and B₂ form the matrix problem II from [5] and so the (D,O)-species with diagram (2.7) is of unbounded representation type.

Lemma 2.8. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4,5}. Then a (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(2.9)

is of unbounded representation type.

Proof. Write J = {1,2,3,4}. Let X be a right O-module, let Y_i be a right D-vector space for iÎJ, and let , (i = 2,3), be D-linear mappings.

Let A_i be the matrices corresponding to homomorphisms j_i (i Î J) that define the representation M, and (iÎ J ) be the matrices corresponding to the represen- tation M¢. If UÎM_n(O) is the matrix corresponding to the isomorphism a, and are the matrices corresponding to the isomorphisms b_i, iÎ J, then we have the following matrix equalities:

,

(2.10)

.

(2.11)

We obtain the following matrix problem:

Given a block-rectangular matrix T = which partitioned into 2 horizontal and 3 vertical strips. The following transformations are admitted:

1. Right O-elementary transformations of columns within the first vertical strip of T.

2. Right D-elementary transformations of columns within the second and third vertical strips of T.

3. Left D-elementary transformations of rows within each horizontal strip of T.

Reduce A₂ and A₄ to the form and A₃ to the form

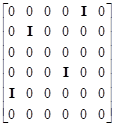In according with this reducing the matrix A₁ is divided into 6 horizontal strips and we obtain the following matrix problem.

Given a block-rectangular matrix B partitioned into 6 vertical strips:

The following transformations are admitted:

1. Left O-elementary transformations of rows of B.

2. Right D-elementary transformations of columns within each vertical strip B_i (i = 1,2,..,6).

3. If a_i £ a_j in the poset S:

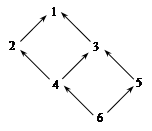
then any column of the vertical strip B_i multiplied on the right by the arbitrary element of D can be added to any column of the vertical strip B_j.

It is easy to see that the blocks B₂, B₄, B₅ form the matrix problem II from [5]. Therefore the species with diagram (2.9) is of unbounded representation type.

Analogously one can prove the following lemma:

Lemma 2.12. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4,5}. Then a (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(2.13)

is of unbounded representation type for any directions of arrows.

Lemma 2.14. Let O_i be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical R_i = p_iO_i = O_ip_i, for i = 1,2; and I = {1,2,3,4}. Then a (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

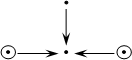(2.15)

is of unbounded representation type.

Proof. Write J = {1,2,3}. Let X_i be a right O_i-module for i = 1,2; Y_j a right D-vector space for j = 1,2; and let , (i = 1,2), be D-linear mappings.

If M = (X₁, X₂, Y₁, Y₂, j_i,)_{i ÎJ} and M¢ = (X₁¢, X₂¢, Y₁¢, Y₂¢, j¢_i,)_{i ÎJ} are two equivalent representations of a (D,O)-species W and a_i: X_i ® X_i¢ are isomorphisms of O-modules, b_i: Y_i ® Y¢_i are isomorphisms of D-vector spaces (i = 1,2), then the following equalities hold:

(2.16)

(2.17)

Let A_i be the matrices corresponding to the homomorphisms j_i (i Î J) that define the representation M, and (iÎ J) be the matrices corresponding to the representation M¢. If U_i is the matrix with entries in O_i corresponding to the isomorphism a_i, and are the matrices corresponding to the iso- morphisms b_i (i = 1,2), then equalities (2.16) and (2.17) have the following matrix form:

(2.18)

.

(2.19)

We obtain the following matrix problem:

Given a block-rectangular matrix T = . The following transformations are admitted:

1. Left D-elementary transformations of rows of T.

2. Right O₁-elementary transformations of columns of A₁.

3. Right O₂-elementary transformations of columns of A₂.

4. Right D-elementary transformations of columns of A₃.

Consider two possible cases.

Case 1: Assume that O₁ = O₂. Set

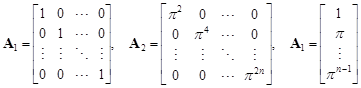By [5, lemma 3], the matrix T is indecomposable. Thus the corresponding representation M of the species W is indecomposable and the species W with diagram (2.15) is of unbounded representation type.

Case 2: Assume that O₁ ¹ O₂. Set A₁ = A₂ = I. Then T = and for the matrix A₃ we have the matrix problem II from [6]. By [6, Lemma 4.2], this matrix problem is of unbounded representation type. Therefore, the species with diagram (2.15) is of unbounded representation type.

Lemma 2.20. Let O_i be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical R_i = p_iO_i = O_ip_i, for i = 1,2; and I = {1,2,3,4}. Then a (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

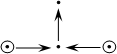(2.21)

is of unbounded representation type.

This lemma is proved as Lemma 2.14.

Note that all diagrams which are not presented in the diagrams of Theorem 1 have a subdiagram of one of the types considered in this section and hence they are of bounded representation type. Therefore, the necessity of Theorem 1 follows from Lemmas 2.1, 2.6, 2.8, 2.12, 2.14, 2.20 and [4, proposition 4.4].

3. Proof of the sufficiency in Theorem 1

Lemma 3.1. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, and let I = {1,2,…,n, n+1}. Then a weak (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(3.2)

is of bounded representation type.

Proof. Write J = {1, 2, ... , n}. Let X be a right O-module, let Y_i be a right D-vector space for i Î J, and let ; be D-linear mapping for i = 2, ..., n.

If M = (X, Y_i, j_i)_{i ÎJ} and M¢ = (X¢, Y¢_i, j¢_i)_{i ÎJ} are two equivalent representations of a (D,O)-species W, a: X ® X¢ is an isomorphism of O-modules and b_i: Y_i ® Y¢_i are isomorphisms of D-vector spaces (i Î J), then the following equalities hold:

,

(3.3)

.

(3.4)

Let A_i be the matrices corresponding to the homomorphisms j_i (i Î J) that define the representation M, and (iÎ J) be the matrices corresponding to the representation M¢. If UÎM_s(O) is the matrix corresponding to the isomorphism a, and are the matrices corresponding to the isomorphisms b_i (iÎ J), then equalities (3.3) and (3.4) have the following matrix form:

(3.5)

Note that the problem of reducing a set of matrices A_i by matrices V_i (i = 2, ..., n) satisfying equalities (3.5) leads to the problem of classifying representations of the quiver Q with diagram A_n-1. By the Gabriel theorem [1], this quiver has indecomposable representations. In accordance with these representations, the matrix A₁ is partitioned into 2n-2 vertical strips, and the partial ordering relation between these strips is linear. Therefore, the matrix problem (3.5) leads to the following matrix problem.

Given a rectangular matrix T with entries in a skew field D that is partitioned into 2n-2 vertical strips:

The transformations of the following types are admitted:

1. Right O-elementary transformations of rows of T.

2. Left D-elementary transformations of columns within each vertical strip T_i.

3. Addition of columns of the i-th vertical strip T_i multiplied on the right by elements of D to columns in the j-th vertical strip T_j if i £ j.

The matrix T can be reduced by these transformations to the form in which any block T_i has the form and all blocks over and under I are zero. Thus, for any indecomposable representation M the corresponding matrix T has a finite fixed number of nonzero elements and this number depends only on n. Therefore, the species W with diagram (3.2) is of bounded representation type.

Lemma 3.6. Let O_i be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical R_i = p_iO_i = O_ip_i for i = 1,2; and let I = {1,2,..., n, n +1}. Then a weak (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(3.7)

is of bounded representation type.

Proof. Renumber the vertices of the diagram (2.16) in such a way that the vertex 1 corresponds to F₁ = O₁ and the vertex 2 corresponds to F₂ = O₂. We obtain the diagram

Write J = {1, 2, ..., n–1}. Let X_i be a right F_i-module (i = 1,2), let Y_j be a right D-vector space for j Î J, and let ; ; be D-linear mapping for i = 2, ..., n-1.

If M = (X₁, X₂, Y_i, j_i, j_n)_{i ÎJ} and M¢ = (X₁¢, X₂¢, Y¢_i, j¢_i, j_n¢)_{i ÎJ} are two equivalent representations of a (D,O)-species W and a_i : X_i ® X_i¢ is an isomorphism of O-modules (i = 1,2), b_j : Y_j ® Y¢_j is an isomorphism of D-vector spaces (j Î J), then the following equalities hold:

(3.8)

(3.9)

Suppose the isomorphism a_i is given by the matrix U_i with entries in O_i for i = 1,2; and the isomorphism b_j is given by the matrix V_j with entries in D for j Î J. If A_i, (i Î I) are the matrices corresponding to the representations M, M¢ then equalities (3.8) and (3.9) are equivalent to the following matrix equalities:

(3.10)

(3.11)

Note that the reduction of a set of matrices A_i, i = 1,3,4, ..., n, by admissible transformations (3.10) and (3.11) leads to the matrix problem of classifying representations of a (D,O)-species W with diagram (3.2) described in Lemma 3.1. After reducing the matrices A_i, i = 1,3,4, ..., n, we get A₂ partitioned into n vertical strips and the following matrix problem for A₂.

Given a block matrix T with entries in a skew field D that is partitioned into n vertical strips:

The transformations of the following types are allowed:

1. Left O₂-elementary transformations of rows of T.

2. Right O₁-elementary transformations of columns within a vertical strip T_k, for some fixed 1 £ k £ n.

3. Right D-elementary transformations of columns within each vertical strip T_i, if i ¹ k.

4. Addition of columns in the vertical strip T_i multiplied on the right by elements of D to columns in the vertical strip T_j if i £ j.

Using these transformations and taking into account [5, Lemma 4.1], we can reduce T to the form in which every block T_i has the form: U = or W = and all matrices over, under, on the left, and on the right of the matrix I or, respectively, p^mI are zero. This means that the matrix A₂ is decomposed into a direct sum of matrices of the forms U and W.

Thus, the species W with diagram (3.7) is of bounded representation type.

Analogously we can prove the following lemma:

Lemma 3.12. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, and let I = {1,2,…,n, n+1}. Then a weak (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(3.13)

is of bounded representation type.

Lemma 3.14. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, and I = {1,2,…,n, n+1}. Then a weak (D,O)-species W = (F_i, _iM_j)_{i,j Î I} whose diagram with weights has the form

(3.15)

is of bounded representation type.

Proof. Write J = {1,2}. Let X be a right O-module, let Y_i be a right D-vector space, and let be a D-linear mapping for i Î J.

If M = (X, Y_i, j_i)_{i ÎJ} and M¢ = (X¢, Y¢_i, j¢_i)_{i ÎJ} are two equivalent representations of a (D,O)-species W and a: X ® X¢ is an isomorphism of O-modules, b_i : Y_i ® Y¢_i are isomorphisms of D-vector spaces (i Î J), then the following equalities hold:

(3.16)

Let U Î M_s(O) be the matrix corresponding to the isomorphism a, and let be the matrices corresponding to the isomorphisms b_i, iÎ J. If A_i, (i Î J) are the matrices corresponding to the representations M, M¢ then equalities (3.14) are equivalent to the following matrix equalities

(3.17)

We obtain the following matrix problem.

Given a matrix T = with entries in D. The transformations of the follow- ing types are allowed:

1. Right D-elementary transformations of columns within any vertical strip.

2. Left O-elementary transformations of rows of T.

The matrix T can be reduced by these transformations to a direct sum of the following matrices:

, , , .

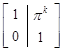Thus, a (D,O)-species with diagram (3.15) is of bounded representation type.

The sufficiency in Theorem 1 follows from Lemmas 3.1, 3.6, 3.12, and 3.16.

4. Conclusion

We have described all weak (D, O)-species of bounded representation type. The proof is given by reduction to mixed matrix problems over discrete valuation rings and their common skew field of fractions. We use some facts about representations of quivers and species from [1-3].

References

[1] Gabriel P., Indecomposable representations I, Manuscripta Math. 1972, 6, 71-103.

[2] Dlab V., Ringel C.M., On algebras of finite representation type, Journal of Algebra 1975, 33, 306-394.

[3] Dowbor P., Ringel C.M., Simson D., Hereditary Artinian rings of finite representation type, Representation theory, II. Lecture Notes in Math. 1980, 832, 232-241.

[4] Gubareni N., Representations of (D,O)-species and flat mixed matrix problems, Journal of Applied Mathematics and Computational Mechanics 2016, 3(15), 47-56.

[5] Gubareni N., Structure of finitely generated modules over right hereditary SPSD-rings, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 45-56.

[6] Gubareni N., Some mixed matrix problems over several discrete valuation rings, Journal of Applied Mathematics and Computational Mechanics 2013, 4(12), 47-58.