Novel visual object descriptor using SURF and clustering algorithms

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Grycuk_2016,
   doi = {10.17512/jamcm.2016.3.04},
   url = {https://doi.org/10.17512/jamcm.2016.3.04},
   year = 2016,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {15},
   number = {3},
   pages = {37--46},
   author = {Rafał Grycuk},
   title = {Novel visual object descriptor using SURF and clustering algorithms},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2016.3.04
UR  - https://doi.org/10.17512/jamcm.2016.3.04
TI  - Novel visual object descriptor using SURF and clustering algorithms
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Grycuk, Rafał
PY  - 2016
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 37
EP  - 46
IS  - 3
VL  - 15
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Grycuk, R. (2016). Novel visual object descriptor using SURF and clustering algorithms. Journal of Applied Mathematics and Computational Mechanics, 15(3), 37-46. doi:10.17512/jamcm.2016.3.04

Grycuk, R., 2016. Novel visual object descriptor using SURF and clustering algorithms. Journal of Applied Mathematics and Computational Mechanics, 15(3), pp.37-46. Available at: https://doi.org/10.17512/jamcm.2016.3.04

[1]R. Grycuk, "Novel visual object descriptor using SURF and clustering algorithms," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 3, pp. 37-46, 2016.

Grycuk, Rafał. "Novel visual object descriptor using SURF and clustering algorithms." Journal of Applied Mathematics and Computational Mechanics 15.3 (2016): 37-46. CrossRef. Web.

1. Grycuk R. Novel visual object descriptor using SURF and clustering algorithms. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(3):37-46. Available from: https://doi.org/10.17512/jamcm.2016.3.04

Grycuk, Rafał. "Novel visual object descriptor using SURF and clustering algorithms." Journal of Applied Mathematics and Computational Mechanics 15, no. 3 (2016): 37-46. doi:10.17512/jamcm.2016.3.04

NOVEL VISUAL OBJECT DESCRIPTOR USING SURF AND CLUSTERING ALGORITHMS

Rafał Grycuk

Institute of Computational Intelligence, Czestochowa University of Technology
Częstochowa, Poland
rafal.grycuk@iisi.pcz.pl

Abstract. In this paper we propose a method for object description based on two well-known clustering algorithms (k-means and mean shift) and the SURF method for keypoints detection. We also perform a comparison of these clustering methods in object description area. Both of these algorithms require one input parameter; k-means (k, number of objects) and mean shift (h, window). Our approach is suitable for images with a non-homogeneous background thus, the algorithm can be used not only on trivial images. In the future we will try to remove non-important keypoints detected by the SURF algorithm. Our method is a part of a larger CBIR system and it is used as a preprocessing stage.

Keywords: k-means, mean shift, clustering, image description, SURF, keypoints, CBIR

1. Introduction

Content-based image retrieval is one of the greatest challenges of present computer science. Effective browsing and retrieving of images is required in various fields of life e.g. medicine, architecture, forensic, publishing, fashion, archives and many others. In the process of image recognition, users search through databases which consist of thousands, even millions of images. The purpose of CBIR is to retrieve a similar image or images containing certain objects from the query image [1, 2]. A process associated with retrieving images in the databases is query formulation (just like the ‘select’ statement in the SQL language). In the literature, it is possible to find algorithms which operate on one of the three levels [3]:

· Level 1: Retrieval based on primary features like color, texture and shape. A typical query is “search for a similar image”.

· Level 2: Retrieval of a certain object which is identified by extracted features, e.g. “search for a flower image”.

· Level 3: Retrieval of abstract attributes, including vast number of determiners about presented objects and scenes. Here, it is possible to find names of events and emotions. An exemplary query is: “search for angry people”.

Such methods require the use of algorithms from many different areas such as computational intelligence [4], mathematics and image processing. All of them allow it to perform mathematical description of the image [5, 6]. For example, they extract primary features such as: color [7, 8], texture, shape [9] and their position on the image. The features can be subjected to additional algorithms which are able to reduce their number. It is possible, thanks to exclusion of background elements, to eliminate the features absent in other images with the same object. In this paper we present a novel approach for image description based on a SURF algorithm and two well-known clustering methods: k-means and mean shift.

1.1. SURF

SURF (Speeded-Up Robust Features) is an algorithm which makes it possible to detect and describe local features of an image. It was presented for the first time in [10], but currently is used in various systems e.g. image recognition, 3D reconstruction, image description, segmentation [11], image analysis [12], content based image retrieval [13], object tracking, image databases [14], and many others. SURF is based on SIFT, and it uses Integral Images instead of DOG (Difference of Gaussian), which allows it to work much faster than SIFT. It can also be accelerated by GPU and it has a parallel implementation. SURF is based on image keypoints (interesting points), which makes it possible to extract local features from an image. For each keypoint, which indicates local image feature, we generate a feature vector, which can be used for further processing. SURF consists of four main steps:

· Computing Integral Images,

· Fast-Hessian Detector,

o The Hessian,

o Constructing the Scale-Space,

o Accurate Interest Point Localization,

· Interest Point Descriptor,

o Orientation Assignment,

o Descriptor Components,

· Generating vectors describing the keypoint.

A SURF keypoint consists of two vectors [15, 16]. The first one contains: point position (x, y), scale (Detected scale), response (Response of the detected feature, strength), orientation (Orientation measured anti-clockwise from +ve x-axis), laplacian (Sign of laplacian for fast matching purposes). The second one describes the intensity distribution of the pixels within the neighborhood of the interest point (64 or 128 values). In order to generate keypoints, SURF requires one input parameter minHessian. The method is resistant to change of scale and rotation, which allows for matching corresponding keypoints in similar images [17].

1.2. Mean shift clustering method

The mean shift clustering algorithm [18] is a method which does not require any parameters such as cluster number or shape. The number of parameters of the algorithm is limited to the radius h, that number determines the range of the clusters [19]. The mean shift determines the points in d-dimensional space as a probability density function, where the denser regions correspond to local maxima. For each data point in the feature space, one performs a gradient ascent procedure on the local estimated density until convergence. Points assigned to one cluster (stationary point) are considered to be a part of the cluster. Given points multivariate kernel density function is expressed using the following equation [20]:

(1)

where defines the radius of the kernel function. The kernel function is defined as

(2)

where represents a normalization constant. With a density gradient estimator we can make the following calculations [20]:

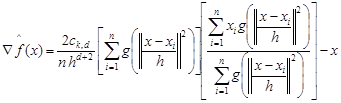(3)

where denotes the derivative of a function of the selected kernel. The first term1 allows one to determine the density, while the second term2 defines a mean shift vector m(x). Where m(x) is vector and t is algorithm step. Points toward the direction of the maximum density and proportional to the density gradient can be determined at the point t, obtained with kernel function K. The algorithm can be summarized in the following steps [20]:

· Determine the mean shift vector, expressed by formula:

· Translate density estimation window:

· Repeat the first and the second step until:

1.3. K-means Clustering Method

K-means algorithm belongs to the group of heuristic clustering algorithms. It was firstly proposed by MacQueen in 1967 [21] and improved by Hartigan in 1979 [22]. The purpose of this method is to divide N points in D dimensional space into K clusters. That process of partitioning requires only one input parameter K - number of clusters. K-means is commonly used for data clustering in various applications. It is relatively fast and easy in implementation. The following pseudo-code describes its functioning [23, 24]:

INPUT: (data to cluster), k (number of clusters)

OUTPUT: (cluster centers),

1. Create random initial cluster centers,

2. ForEach do

{

Set ;

}

3. Set ch := false;

4. While ch = true

{

ForEach do

{

UpdateCluster();

}

ForEach do

{

Set minDistance := ArgMinDist;

If minDistance ≠ then

{

Set ;

Set ch := true

}

}

}

The results of k-means are presented in Figure 1. As can be seen, the input data were clustered and presented as simple shapes. The parameter k was set to 6.

Fig. 1. An example of the k-means clustering. The left side of the image presents input data, the right side shows the clusters. Each shape is a different cluster

2. Presented method for image keypoint clustering

The presented method is based on three well-known algorithms: SURF [25-27], Mean Shift and K-Means. In this paper we compare efficiency of clustering algorithms in the field of visual object extraction [28, 29]. This work is a description of pre-processing implemented in our system. The input images need to be indexed, thus first we need to extract the local features of the image. There are many methods for feature extraction, but in this paper we used SURF (see Subsection 1.1). For each image we perform a smooth (Gaussian blur) operation to remove non important features. Then, we execute the SURF algorithm with minHessian set to 500. On the output we obtain a list of keypoints. Each keypoint contains two vectors. From the first vector we get the position of the keypoint. In the next step we perform the keypoint clustering (both k-means and mean shift separately). Each keypoint is assigned to the cluster to which it belongs. Our method allows one to extract keypoints located on the objects, and remove most of the features not related with the object. It also performs keypoint segmentation, thus the object has assigned a list of keypoints. This pre-processing step is extremely important because it improves the indexation process in our CBIR system (removes non-important features). The presented pseudo-code and block diagram (Fig. 2) show all the steps of our approach.

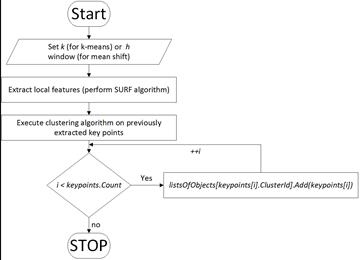
INPUT: Input image, k (number of objects) [or h window for Mean shift]

OUTPUT: List of keypoints assigned to each object

1. keypoints := DetectKeypoints(InputImage);

2. ClusterKeyPoints(keypoints);

3. ForEach keypoints do

{

;

}

3. Experimental results

In this section we present the results of the experiments. The simulation environ- ment was written by the author in .NET Framework with an Emgu CV library and C# programing language. The research includes experiments on various objects with a background. The system firstly detects all the keypoints in the input image (see Fig. 3) then the clustering algorithm can be chosen. Next, the clustering is performed. On the output we obtain the image with clustered keypoints. Clusters are labeled by ASCII characters (e.g. the first cluster is labeled by ‘W’, the second by ‘c’) as can be seen the characters are random, because our algorithm is flexible and we do not know how many clusters will be detected.

Fig. 3. Keypoints detected by the SURF algorithm. The circles represent the position of the keypoints

The presented experiments have proven that k-means is more effective in object description (see Fig. 4). Keypoints are clustered correctly and most of them are located on objects. Figure 5 shows that two objects are placed on points labeled as ‘X’. Other keypoints are also misplaced, or they are detected on the background. Table 1 presents the comparison of both algorithms in the image description.

Fig. 4. Clustered keypoints by k-means algorithm

Fig. 5. Clustered keypoints by the mean shift algorithm

Table 1

Comparison of k-means and mean shift in image description. Percentage value of correct assigned keypoints [%]

As can be seen, the k-means has better performance in seven experiments. Only Experiment 4 provided different results. This is because the mean shift is a density-based algorithm and the image keypoints in Exp. 4 are located in denser regions with a huge distance between them.

4. Conclusions

The presented comparison proves that the k-means algorithm is more suitable for image description purposes. The image descriptor that we obtain allows one to extract object keypoints which is a crucial step in any CBIR method (pre-processing). Our approach returns a list of keypoints assigned to each object located in the input image. Thus, further processing will take under consideration only keypoints located on the interesting object. Unfortunately, SURF detects keypoints outside of object edge, and they need to be removed. This is the only disadvantage of our method. In the future we will try to develop a method that will resolve the issue. The performed experiments proved the effectiveness of our approach.

Acknowledgments

The work presented in this paper was supported by a grant BS/MN-1-109-301/14/P “Clustering algorithms for data stream - in reference to the Content-Based Image Retrieval methods (CBIR)” and by the grant BS/MN-1-109-301/15/P “New approa- ches of storing and retrieving images in databases".

References

[1] Bazarganigilani M., Optimized image feature selection using pairwise classifiers, Journal of Artificial Intelligence and Soft Computing Research 2011, 1, 147-153.

[2] Canny J., A computational approach to edge detection, Pattern Analysis and Machine Intelli-gence, IEEE Transactions 1986, 8(6), 679-698.

[3] Liu Y., Zhang D., Lu G., Ma W.Y., A survey of content-based image retrieval with high-level semantics, Pattern Recognition 2007, 40(1), 262-282.

[4] Gabryel M., Korytkowski M., Scherer R., Rutkowski L., Object detection by simple fuzzy classifiers generated by boosting, Artificial Intelligence and Soft Computing 2013, Springer International Publishing, 540-547.

[5] Nowak T., Najgebauer P., Rygał J., Scherer R., A Novel Graph-Based Descriptor for Object Matching, Artificial Intelligence and Soft Computing 2013, Springer International Publishing, 602-612.

[6] Gabryel M., Korytkowski M., Scherer R., Rutkowski L., Object detection by simple fuzzy classifiers generated by boosting, Artificial Intelligence and Soft Computing 2013, Springer International Publishing, 540-547.

[7] Rygał J., Najgebauer P., Romanowski J., Scherer R., Extraction of objects from images using density of edges as basis for GrabCut algorithm, Artificial Intelligence and Soft Computing 2013, Springer International Publishing, 613-623.

[8] Nowak T., Najgebauer P., Romanowski J., Gabryel M., Korytkowski M., Scherer R., Kosta- dinov D., Spatial keypoint representation for visual object retrieval, Artificial Intelligence and Soft Computing 2014, Springer International Publishing, 639-650.

[9] Rygał J., Romanowski J., Scherer R., Ferdowski S., Novel algorithm for translation from image content to semantic form, Artificial Intelligence and Soft Computing 2014, Springer International Publishing, 783-792.

[10] Bay H., Tuytelaars T., Van Gool L., SURF: Speeded up robust features, Computer Vision-ECCV 2006, 404-417.

[11] Grycuk R., Gabryel M., Korytkowski M., Romanowski J., Scherer R., Improved digital image segmentation based on stereo vision and mean shift algorithm, Parallel Processing and Applied Mathematics 2014, 8384, 433-443.

[12] Grycuk R., Gabryel M., Korytkowski M., Scherer R., Voloshynovskiy S., From single image to list of objects based on edge and blob detection, Artificial Intelligence and Soft Computing 2014, 8468, 605-615.

[13] Grycuk R., Gabryel M., Korytkowski M., Scherer R., Content-based image indexing by data clustering and inverse document frequency, Beyond Databases, Architectures, and Structures 2014, 424, 374-383.

[14] Chromiak M., Stencel K., A data model for heterogeneous data integration architecture, Beyond Databases, Architectures, and Structures 2014, 547-556.

[15] Lowe D.G., Object recognition from local scale-invariant features, Computer Vision 1999, 2, 1150-1157.

[16] Lowe D.G., Distinctive image features from scale-invariant keypoints, International Journal of Computer Vision 2004, 60(2), 91-110.

[17] Evans C., Notes on the Opensurf Library, University of Bristol, Tech. Rep, 2009

[18] Cheng Y., Mean shift mode seeking, and clustering, Pattern Analysis and Machine Intelligence, 1995, 17(8), 790-799.

[19] Derpanis K.G., Mean shift clustering, Lecture Notes, 2005.

[20] Comaniciu D., Meer P., Mean shift: A robust approach toward feature space analysis, Pattern Analysis and Machine Intelligence 2002, 24(5), 603-619.

[21] MacQueen J., Some methods for classification and analysis of multivariate observations, Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability 1967, 1, 281-297.

[22] Hartigan J.A., Wong M.A., Algorithm AS 136: A k-means clustering algorithm, Applied Statistics 1979, 100-108.

[23] Kanungo T., Mount D.M., Netanyahu N.S., Piatko C.D., Silverman R., Wu A.Y., An efficient k-means clustering algorithm: Analysis and implementation, Pattern Analysis and Machine Intelligence 2002, 24(7), 881-892.

[24] Wagstaff K., Cardie C., Rogers S., Schrödl S., Constrained k-means clustering with background knowledge, ICML 2001, 1, 577-584.

[25] Hare J.S., Samangooei S., Lewis P.H., Efficient clustering and quantisation of SIFT features: exploiting characteristics of the SIFT descriptor and interest region detectors under image inversion, Proceedings of the 1st ACM International Conference on Multimedia Retrieval, 2011, 2-18.

[26] Soltanshahi M.A., Montazer G.A., Giveki D., Content based image retrieval system using clustered scale invariant feature transforms, Optik - International Journal for Light and Electron Optics 2015, 126(18), 1695-1699.

[27] Górecki P., Sopyła K., Drozda P., Ranking by k-means voting algorithm for similar image retrieval, In: Artificial Intelligence and Soft Computing 2012, Springer, Berlin Heidelberg, 509-517.

[28] Velmurugan K., Baboo L.D.S.S., Content-based image retrieval using SURF and colour moments, Global Journal of Computer Science and Technology 2011, 11(10).

[29] Zagoris K., Chatzichristofis S.A., Arampatzis A., Bag-of-visual-words vs global image descriptors on two-stage multimodal retrieval, Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval, 2011, 1251-1252.