Comparison of bio-heat transfer numerical models based on the Pennes and Cattaneo-Vernotte equations
Mariusz Ciesielski
,Mateusz Duda
,Bohdan Mochnacki
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
COMPARISON OF BIO-HEAT TRANSFER NUMERICAL MODELS BASED ON THE PENNES AND CATTANEO-VERNOTTE EQUATIONS
Mariusz Ciesielski 1, Mateusz Duda 2, Bohdan Mochnacki 2
1 Institute
of Computer and Information Sciences, Czestochowa University of Technology
Częstochowa, Poland
2 University of Occupational Safety Management in Katowice
Katowice, Poland
mariusz.ciesielski@icis.pcz.pl, bmochnacki@wszop.edu.pl,
mduda@wszop.edu.pl
Received: 07 October
2016; accepted: 10 November 2016
Abstract. The homogeneous soft tissue domain subjected to an external heat source is considered. Thermal processes in this domain are described using the well known Pennes equation and next the Cattaneo-Vernotte one. Within recent years the prevailing view is that the Cattaneo-Vernotte equation better describes the thermal processes proceeding in the biological tissue (it results from the specific internal tissue structure). Appearing in this equation the delay time of heat flux with respect to the temperature gradient (τq) is of the order of several seconds and the different values of τq are taken into account. At the stage of numerical modeling the finite difference method is used. In the final part of the paper, the examples of computations are shown.
Keywords: bioheat transfer, Pennes equation, Cattaneo-Vernotte equation, numerical modeling of heating process, finite difference method
1. Introduction
The heat transfer processes proceeding in the domain of soft tissue are the most commonly described by the well known Pennes equation [1-3]. It is the Fourier - - type PDE containing the additional internal heat sources resulting from the blood perfusion and metabolism. The first is proportional to the local differences between blood and tissue temperatures and the mathematical form of the perfusion heat source results from the assumption that the tissue domain is supplied by a large number of blood capillaries (the soft tissue models). The metabolic heat source can be treated as the temperature dependent function (e.g. [4]) or a constant value (e.g. [5]).
As is generally known, the Fourier-type equation has been formulated under the assumption of the infinite velocity of thermal wave propagation. In the case of materials with a specific internal structure (e.g. biological tissue) this equation should be modified. To take into account the delay effect of the local and temporary heat flux with respect to the temperature gradient, the so-called relaxation time τq is introduced, and then the heat transfer process is described by the Cattaneo- -Vernotte equation (CVE) [6, 7] which belongs to the group of hyperbolic PDE. According to the literature data, the relaxation time for the processed meat is the order of seconds (2÷5 s) [7]. Recently the thermal processes in the domain of soft tissue are also described using the dual phase lag equation in which two delay times are taken into account (the relaxation time τq and a thermalization time τT - e.g. [8, 9]). This approach is very interesting, but so far, the numerical data concerning the delay times are rather precarious.
The interesting thing from a practical point of view is the comparison of the results obtained using both models and also the analysis of the impact of relaxation time changes on the CVE solution.
At the stage of numerical computations, the authorial variant of the finite difference method (FDM) has been used [10]. The 1D problem has been considered. Such a solution is sufficient for the formulation of conclusions connected with the subject of this study. In the final part of the paper the results of numerical simulations and also the concluding remarks are formulated.
2. The governing equations
The 1D Pennes equation for the domain oriented in the Cartesian co-ordinate system can be written in the following form
| (1) |
where c is the volumetric specific heat of tissue, λ is the thermal conductivity, Q is the capacity of internal heat sources, T is the temperature, x, t denote the geometrical co-ordinate and time.
The internal heat source is a sum of two components
| (2) |
where GB [m3blood/m3tissue/s] is the perfusion coefficient, cB is the volumetric specific heat of blood, TB is the arterial blood temperature, and Qmet is the metabolic heat source.
The equation (1) is supplemented by the appropriate boundary and initial conditions. In particular, for x = 0 the value of external heat flux is given (the Neumann boundary condition), meaning
| (3) |
while for x = G (a thickness of domain) the no-flux condition (qb = 0) is assumed.
Additionally, for t = 0
| (4) |
The Cattaneo-Vernotte equation is more complicated, namely
| (5) |
where the relaxation time is denoted by τq. Taking into account the mathematical form of internal heat source (2), one has
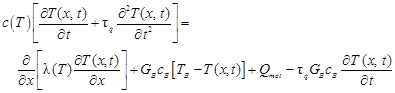 | (6) |
It can be seen that contrary to the parabolic Pennes equation (1), the equation (5) is of the hyperbolic type. As previously expressed, the equation (6) is supplemented by the appropriate boundary and initial conditions. It should be pointed out that the form of typical boundary conditions in the case of CVE is somewhat different than those that are classic. In particular, the Neumann condition takes a form
| (7) |
One can see, that for the constant value of q(x,t)
= qb the condition (7) takes a classical form. The initial
conditions concern the initial tissue temperature (4) and initial heating rate ![]() .
.
3. The numerical solution
The numerical
solution of the problem discussed can be obtained using the explicit scheme of
the FDM. Let us consider the differential mesh being the Cartesian product ![]() , where
, where ![]() and
and
![]() . Both the geometric h and time
∆t mesh steps are assumed to be the constant values.
. Both the geometric h and time
∆t mesh steps are assumed to be the constant values.
Now, the FDM equation for the Pennes model and the set of internal nodes will be presented. To simplify the mathematical notation, the local numbering of nodes is introduced, in particular the numbers 0, 1, 2 correspond to the nodes i, i+1, i–1.
The explicit FDM approximation of the Pennes equation is taken in the form
| (8) |
where (in the case considered)
| (9) |
while Fe, Re are the mesh shape functions and the thermal resistances between the neighboring nodes. In a general case, the formulas determining thermal resistances are essentially more complicated, but here (from the lack of other data) the constant values of c and λ are assumed.
Denoting
| (10) |
one has
| (11) |
or
| (12) |
The stability condition for the explicit FDM scheme is discussed in [11]. The quite simple problem connected with the ‘appending’ of the Neumann boundary conditions will not be presented here.
In the case of the CVE, the numerical model based on the FDM is more complicated, of course. One can refer here to the paper [12] in which the FDM equations for the Cattaneo-Vernotte model are presented in details. Generally speaking, the ‘start point’ for the successive mathematical transformations is the equation
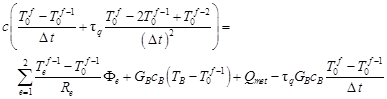 | (13) |
while the symbols appearing in this equation correspond to the symbols used in equation (8). From this three-level FDM explicit differential scheme one can find the values of T0f. The problem of FDM equation stability is discussed in the previously cited work [12].
4. Results of computations
The 1D problem is considered here, the tissue layer (muscle) with a thickness G = 15 mm is subjected to the heat flux qb = 1250 W/m2, while on the boundary x = G the no-flux condition (qb = 0) is assumed. The following thermophysical parameters are accepted: λ = 0.42 W/(mK), c = 3768·1085 J/(m3K), GB = = 0.5380·10‒3 1/s, Qmet = 684 W/m3, cB = 3650·1069 J/(m3K), TB = 37°C. Initial temperature T0 = 35.7°C. In Figures 1 and 2 the examples of the results obtained are shown. The heating curves at the selected points of domain for the Pennes model are presented in Figure 1, while the influence of non-zero value of lag times (τq = 2 s and τq = 5 s) is well visible in Figure 2.
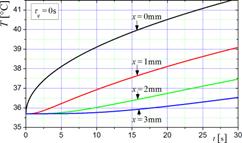
Fig. 1. Solution of the Pennes equation
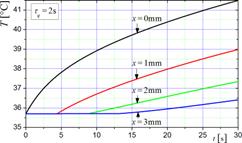
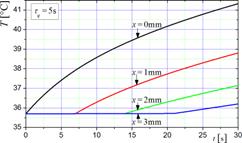
Fig. 2. Solutions of CVE for the relaxation times 2 s and 5 s
5. Final remarks
The differences between
numerical solutions corresponding to the Pennes and Cattaneo-Vernotte models are
clearly visible. They are especially evident
at the
points located in the interior of tissue domain. This can be of
importance, among others,
for the modeling of tissue burns. The residence time at a temperature above 44°C
is very essential at the stage of
burn degree prediction (e.g. [2]). It seems that
the Cattaneo-Vernotte model is closer to the real course of the
process and can be widely used for the modeling of bioheat transfer
problems. One can note that the results obtained for the Cattaneo-Vernotte
model clearly illustrate the existence of a thermal wave front. This front moves
with the finite velocity ![]() [m/s]. For the assumed lag times (τq = 2 s
and τq = 5 s),
the velocities are equal to
0.227 mm/s, and 0.143 mm/s, respectively.
[m/s]. For the assumed lag times (τq = 2 s
and τq = 5 s),
the velocities are equal to
0.227 mm/s, and 0.143 mm/s, respectively.
Acknowledgement
This work is supported by the project No. 2015/19/B/ST8/01101 sponsored by The National Science Centre (Poland).
References
[1] Pennes H.H., Analysis of tissue and arterial blood temperatures in the resting human forearm, J. Appl. Physiol. 1948, 1, 93-122.
[2] Majchrzak E., Mochnacki B., Jasinski M., Numerical modelling of bioheat transfer in multi-layer skin tissue domain subjected to a flash fire, Computational Fluid and Solid Mechanics 2003, 1-2, 1766-1770.
[3] Jasinski M., Modelling of tissue thermal injury process with application of direct sensitivity method, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 947-957.
[4] Majchrzak E., Modelowanie i analiza zjawisk termicznych, Rozdział 4, Biomechanika, Tom XII Mechanika Techniczna, Ed. R. Bedzinski, IPPT PAN, 2011, 223-362.
[5] Ciesielski M., Mochnacki B., Application of the control volume method using the Voronoi polygons for numerical modeling of bio-heat transfer processes, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 927-935.
[6] Cattaneo M.C., A form of heat conduction equation which eliminates the paradox of instantaneous propagation, C.R. Acad. Sci. I - Math., 1958, 247, 431-433.
[7] Antaki P.J., New interpretation of non-Fourier heat conduction in processed meat, ASME J. Heat Transfer 2005, 127, 189-193.
[8] Majchrzak E., Numerical solution of dual phase lag model of bioheat transfer using the general boundary element method, CMES - Computer Modeling in Engineering & Sciences 2010, 69, 1, 43-60.
[9] Majchrzak E., Turchan L., The general boundary element method for 3D dual-phase lag model of bioheat transfer, Engineering Analysis with Boundary Elements 2015, 50, 76-82.
[10] Mochnacki B., Computational simulations and applications. Numerical modeling of solidification process (Chapter 24), Ed. Jianping Zhu, INTECH, 2011, 513-542.
[11] Tuzikiewicz W., Duda M., Bioheat transfer equation. The problem of FDM explicit scheme stability, Journal of Applied Mathematics and Computational Mechanics 2015, 14(4), 139-144.
[12] Mochnacki B., Tuzikiewicz W., Cattaneo-Vernotte bioheat transfer equation. Stability conditions of numerical algorithm based on the explicit scheme of finite difference method, Journal of Applied Mathematics and Computational Mechanics 2016, 15(4), 137-144.

