The Jacobians of non-maximal degree
Sylwia Lara-Dziembek
,Grzegorz Biernat
,Edyta Pawlak
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE JACOBIANS OF NON-MAXIMAL DEGREE
Sylwia Lara-Dziembek, Grzegorz Biernat, Edyta Pawlak
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
sylwia.lara@im.pcz.pl, grzegorz.biernat@im.pcz.pl, edyta.pawlak@im.pcz.pl
Received: 30 October
2016; accepted: 15 November 2016
Abstract. In the article the leading forms of the polynomial mapping having the Jacobians of non-maximal degree are considered. In particular, the mappings having two zeros at infinity are discussed.
Keywords: Jacobian, zeros at infinity
1. Introduction
The article presents the decomposition of leading forms of the polynomial mapping of two complex variables in the case when the Jacobian of this mapping does not meet maximal degree. In particular, the structure of these forms interest us in the case where the mapping has two zeros at infinity.
2. The Jacobian having non-generic degrees
Let fm, hn be
the forms of variables X, Y of degrees m, n respectively
with
the condition ![]() .
Suppose that the Jacobian of forms fm, hn vanish and
represent the structures of these forms.
.
Suppose that the Jacobian of forms fm, hn vanish and
represent the structures of these forms.
Lemma. Let ![]() . Therefore
. Therefore
| (1) |
and
| (2) |
where:
![]() and
and ![]() ,
, ![]() ,
, 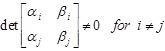 , where
, where ![]() means
the greatest common divisor
of the numbers m and n.
means
the greatest common divisor
of the numbers m and n.
Proof.
According to the Euler formula [1] we have
| (3) |
so using the Cramer rule we obtain
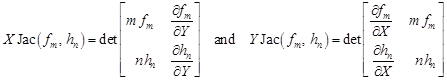 | (4) |
Because ![]() ,
then
,
then
| (5) |
so after dividing by the greatest common divisor (m, n) of the numbers m and n we receive
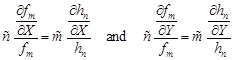 | (6) |
This means that the logarithmic derivatives of the form fm, hn respectively, satisfy equalities
| (7) |
therefore
| (8) |
Thus the forms fm, hn have the same factors.
So
| (9) |
and
| (10) |
According to formula (9) the exponents ![]() satisfy the equalities
satisfy the equalities
| (11) |
Since the numbers ![]() are
relatively prime numbers, then
are
relatively prime numbers, then
| (12) |
So
| (13) |
therefore
| (14) |
and at the
same time the equality ![]() hold.
hold.
This means that
| (15) |
and
| (16) |
Assume
| (17) |
| (18) |
where ![]() .
.
Therefore
| (19) |
so
| (20) |
Thus ![]() exactly when
exactly when ![]() . However
. However
| (21) |
and
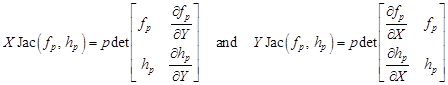 | (22) |
Then
| (23) |
so
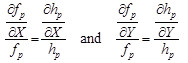 | (24) |
This means that
| (25) |
therefore
| (26) |
This completes the proof.
Remark 1. Obviously
we can assume that ![]() .
.
Corollary
1 [2]. Let ![]() , where
, where ![]() . If
. If ![]() , then only zeros
at infinity of the mapping (f, h) are the factors
of the form fm or hn.
, then only zeros
at infinity of the mapping (f, h) are the factors
of the form fm or hn.
Corollary
2. If the
numbers m and n are relatively prime and ![]() , then
, then ![]() and
and ![]() . This means that the mapping
(f, h) has only one zero at infinity.
. This means that the mapping
(f, h) has only one zero at infinity.
Corollary
3. Let ![]() , where
, where ![]() . Let
. Let ![]() . If the mapping (f,
h) have two zeros at infinity, then
. If the mapping (f,
h) have two zeros at infinity, then
| (27) |
where ![]() , k and l are relatively prime,
, k and l are relatively prime, ![]() .
.
Remark 2. In particular, can be consider the case ![]()
![]() (we put k = l = 1, p = k
+1, q = k). The mappings of this type were considered in the
paper [3].
(we put k = l = 1, p = k
+1, q = k). The mappings of this type were considered in the
paper [3].
3. Conclusion
The Jacobians of non-maximal degree appears for the mappings with the constant Jacobian. The Jacobians Conjecture [4-9] do not occur for non trivial classes of the mappings having the constant Jacobian and one or two zeros in infinity [3, 10]. In the second case (two zeros in infinity) the leading forms of the mapping have the form given in the Corollary 2. The study of such mappings lead to the general classes of the mappings for which the Jacobian Conjecture does not take place.
References
[1] Mostowski A., Stark M., Elementy algebry wyższej, Wyd. Naukowe PWN, Warszawa 1997.
[2] Biernat G., The Jacobians of Lower Degree, Scientific Research of the Institute of Mathematics and Computer Science 2003, 2(1), 19-24.
[3] Lara-Dziembek S., Biernat G., Pawlak E., Woźniakowska M., A second example of non-Keller mapping, Journal of Applied Mathematics and Computational Mechanics 2016, 15(2), 65-70.
[4] Griffiths P., Harris J., Principles of Algebraic Geometry, New York 1978.
[5] Mumford D., Algebraic Geometry I: Complex Projective Varieties , Springer Verlag, New York 1975.
[6] Shafarevich I.R., Basic Algebraic Geometry, Berlin, Springer-Verlag, New York 1974.
[7] Wright D., On the Jacobian conjecture, no. 3, 423-440, Illinois J. Math. 25, 1981.
[8] Van den Essen A., Polynomial automorphisms and the Jacobian conjecture, Progress in Matematics 190, Birkhäuser Verlag, Basel 2000.
[9] Bass H., Connell E.H., Wright D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, American Mathematical Society. Bulletin. New Series 1982, 7(2), 287-330.
[10] Pawlak E., Lara-Dziembek S., Biernat G., Woźniakowska M., An example of non-Keller mapping, Journal of Applied Mathematics and Computational Mechanics 2016, 15(1), 115-121.

