Vibration analysis of composite circular and annular membranes
Urszula Siedlecka
,Izabela Zamorska
,Stanisław Kukla
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
VIBRATION ANALYSIS OF COMPOSITE CIRCULAR AND ANNULAR MEMBRANES
Urszula Siedlecka, Izabela Zamorska, Stanisław Kukla
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
urszula.siedlecka@im.pcz.pl, izabela.zamorska@im.pcz.pl, stanislaw.kukla@im.pcz.pl
Abstract. In this paper a solution to the free vibration problem of composite circular and annular membranes is presented. The vibrations of membranes whose material densities and/or thicknesses varied step-wise with the radial co-ordinate are considered. This approach is applied to approximate the solution to the vibration problem of a membrane with continu- ously varying density and/or thickness with the radial co-ordinate. The obtained analytical solutions are used in numerical investigations into the effect of parameters characterizing the composite membranes on their eigenfrequencies.
Keywords: composite membrane, free vibration, Green’s function
1. Introduction
The vibration analysis of membranes is of particular interest in the design of various acoustical devices. The solution to the vibration problem of a non-homogenous membrane in a closed form can be derived only for the cases of some functions describing the change in the material density and thickness of this membrane. Free vibration problems of circular and annular membranes when the density varies with the radial co-ordinate are the subject of papers [1-5]. The solution to the vibration problem of a membrane comprising two concentric annular membranes has been derived in an exact form by Laura et al. in paper [1]. Gottlieb [2] gives the explicit values of the radial spectrum of an annular membrane with a stepped density which contains inverse fourth power logarithmic terms in the density function. The exact solutions to both the axisymmetric and antisymmetric modes of non-homogenous circular and annular membranes with polynomial variation of the density are given by Jabareen and Eisenberger in paper [3]. The eigenfrequencies for variable density membranes are obtained by a power series expansion and for multiple-connected regions by the dynamic stiffness method.
Approximate methods have been applied to solve the vibration problems of non-homogeneous membranes in numerous papers (for example in references [4-9] various approximate methods are used). An application of the boundary point collocation method to determine the eigenfrequencies of membranes with varying mass density is presented by Cap in paper [4]. Gutierrez et al. [5] present numerical results for two lower free vibration frequencies of circular and annular membranes whose densities varied linearly, quadratically or cubically with the radial coordinate. The frequencies were calculated by using the differential quadrature method, the finite element technique, an optimized and/or improved Rayleigh quotient method and a lower bound based on the Stodola-Vianello method. The multi-symplectic methods for free vibration of the membrane are proposed by Wei-Peng et al. in paper [6]. Numerical results presented in the paper verify the efficiency of the methods. The free vibration frequencies of an annular membrane for axisymmetric modes by the discrete singular convolution method, based on the regularized Shannon’s delta kernel, were determined by Civalek and Gürses in reference [7]. The numerical technique for problems of free vibrations of non-homogenous membranes is presented by Reutskiy in paper [8]. The method is based on the mathematical modeling of the response of a system to external excitation over a range of frequencies. Buchanan [9] has studied vibrational properties and has demonstrated the accuracy of finite element formulation for circular and annular membranes with density variation assumed as a linear function of the radius. The free vibration of an annular membrane consisting of three concentric annular membranes was considered in the paper [10]. The solution of the problem has been derived by using the properties of Green’s functions.
In this paper, a solution to the free vibration problem of composite circular and annular membranes whose densities and/or thicknesses varied step-wise with the radial co-ordinate is derived. This approach has been applied for numerical computation of eigenfrequencies of membranes with a continuous change in density and thickness in the radial direction.
2. Formulation and solution to the free vibration problem of a composite membrane
Consider the vibration problem of an annular
composite membrane consisting of m annular homogenous membranes as shown
in Figure 1. The thickness and
the material density of the composite membrane change step-wise at circles with
radii ![]() . The j-th annular membrane
includes an elastic support distributed along the circle
. The j-th annular membrane
includes an elastic support distributed along the circle ![]() , where
, where ![]() .
.
Free vibrations of the homogenous annular membranes with an elastic support are governed by the following differential equations:
| (1) |
where ![]() is
the displacement of the j-th annular membrane,
is
the displacement of the j-th annular membrane, ![]() is the tension per unit length,
is the tension per unit length, ![]() is the mass per unit area,
is the mass per unit area, ![]() is the thickness of the j-th annular membrane,
is the thickness of the j-th annular membrane,
![]() is the Laplacian operator,
is the Laplacian operator, ![]() and
and ![]() are
polar coordinates and
are
polar coordinates and ![]() is time. The radial variable
is time. The radial variable ![]() for the j-th annular membrane is
in the interval:
for the j-th annular membrane is
in the interval: ![]() ,
, ![]() ,
where
,
where ![]() ,
, ![]() .
.
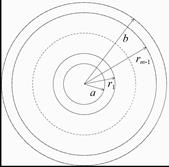
Fig. 1. The sketch of the composite annular membrane under study
Functions ![]()
![]() satisfy
the continuity conditions
satisfy
the continuity conditions
| (2) |
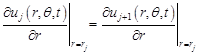 , , | (3) |
and the boundary conditions
| (4) |
Considering the free vibration of the
membrane we assume functions ![]() in
the form
in
the form
| (5) |
where ![]() is
the natural frequency of the composite membrane. Taking equation (6) into
account in differential equation (1), in continuity conditions (3)-(4) and
in boundary conditions (5), we obtain a differential
equation, continuity conditions and boundary conditions for functions
is
the natural frequency of the composite membrane. Taking equation (6) into
account in differential equation (1), in continuity conditions (3)-(4) and
in boundary conditions (5), we obtain a differential
equation, continuity conditions and boundary conditions for functions ![]() :
:
| (6) |
| (7) |
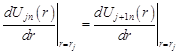 , , | (8) |
![]() (9)
(9)
where ![]() .
.
The general solution of the differential equation (7) is given by
| (10) |
where ![]() and
and ![]() are arbitrary constants.
Substituting the functions (10) into conditions (7)-(9), we obtain a set of
are arbitrary constants.
Substituting the functions (10) into conditions (7)-(9), we obtain a set of ![]() equations which can be written in
a matrix form
equations which can be written in
a matrix form
| (11) |
where ![]() , and
, and ![]() . For
. For ![]() (an
annular membrane) the non-zero elements of the matrix A are (index n
is omitted)
(an
annular membrane) the non-zero elements of the matrix A are (index n
is omitted)
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
for ![]() and
and
![]() ,
, ![]() .
.
For a nontrivial solution of the equation (11) the determinant of the matrix A is set equal to zero yielding the frequency equation of the composite membrane
| (12) |
The equation (12)
is then solved numerically with respect to ![]() by
using an approxi-
mate method. Note that for a fixed
by
using an approxi-
mate method. Note that for a fixed ![]() we obtain a sequence
we obtain a sequence ![]() ,
, ![]() , of
the roots of the equation (12).
, of
the roots of the equation (12).
The frequency equation for a circular
membrane (![]() ) is obtained similarly. In this case,
the first row in the matrix A for the annular membrane should
be changed by assuming:
) is obtained similarly. In this case,
the first row in the matrix A for the annular membrane should
be changed by assuming: ![]() ,
, ![]() . The remainder elements of the matrix A
for the circular membrane are the same as for annular membrane.
. The remainder elements of the matrix A
for the circular membrane are the same as for annular membrane.
For the computed values ![]() ,
, ![]() , the
corresponding
eigenfunctions (the mode shapes of vibration) are given by equation (10) where
the coefficients
, the
corresponding
eigenfunctions (the mode shapes of vibration) are given by equation (10) where
the coefficients ![]() ,
, ![]() are
determined by solving equation (11), in which
are
determined by solving equation (11), in which ![]() should
be assumed. The eigenfunctions satisfied the following orthogonality conditions
should
be assumed. The eigenfunctions satisfied the following orthogonality conditions
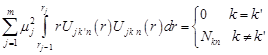 | (13) |
where ![]() and
and
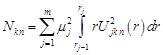 | (14) |
3. Forced vibration of a composite membrane
The differential equation to vibration of an annular membrane forced by an outer force is
| (15) |
The functions ![]()
![]() satisfy the continuity conditions (2)-(3)
and
the boundary conditions (4). Moreover, the initial conditions are
satisfy the continuity conditions (2)-(3)
and
the boundary conditions (4). Moreover, the initial conditions are
| (16) |
![]() (17)
(17)
We seek a solution of the problem in the form of a series
| (18) |
where ![]() were derived in
Section 2 (equation (10)) and functions
were derived in
Section 2 (equation (10)) and functions ![]() will
be now determined.
will
be now determined.
Substituting the
function ![]() in the form (18) into equation (15) and
using the orthogonality condition (13), we obtain an equation with unknown
functions
in the form (18) into equation (15) and
using the orthogonality condition (13), we obtain an equation with unknown
functions ![]() in the form
in the form
![]() (19)
(19)
where ![]() and
and ![]() ,
, ![]() for
for ![]() . This equation is complemented by
initial conditions which follow from (16) and (17). Using (18) and (13) one
obtains the initial conditions in the form
. This equation is complemented by
initial conditions which follow from (16) and (17). Using (18) and (13) one
obtains the initial conditions in the form
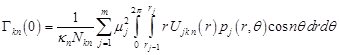 | (20) |
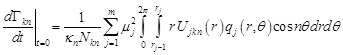 | (21) |
The solution of the equation (19) with conditions (20), (21) is as follows:
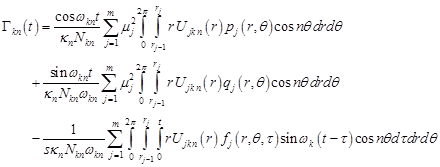 | (22) |
Finally, the solution of the forced vibration problem of the composite membrane can be written in the form
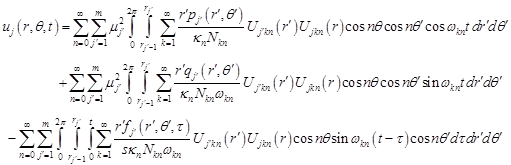 | (23) |
4. Numerical examples
The numerical computations presented here concern the frequency analysis of composite annular and circular membranes for various values of parameters which characterize their non-uniformity. The calculations of the non-dimensional free vibration frequencies were performed using frequency equation (12). The roots of this equation were determined by the application of the false position method [11].
In the first example, the eigenfrequencies of
circular and annular membrane were computed with the density function given by
the formula: ![]() .
The results of calculations:
.
The results of calculations: ![]() (
(![]() ;
;![]() ) for
various values of
) for
various values of ![]() and various numbers of
annular membranes
and various numbers of
annular membranes ![]() are shown
in Table 1 - for the annular membrane and in Table 2 - for the circular membrane. The eigenfrequencies for these membranes
were determined earlier by using
the power series method in paper [3] by Jabareen and Eisenberger. The results
for
are shown
in Table 1 - for the annular membrane and in Table 2 - for the circular membrane. The eigenfrequencies for these membranes
were determined earlier by using
the power series method in paper [3] by Jabareen and Eisenberger. The results
for ![]() , obtained by using the presented
method, are compared with
the results given in reference [3].
The calculated free vibration frequencies
, obtained by using the presented
method, are compared with
the results given in reference [3].
The calculated free vibration frequencies ![]() are consistent
for both annular (Table 1) and circular (Table 2) membranes for
are consistent
for both annular (Table 1) and circular (Table 2) membranes for ![]() and those presented in reference [3].
The differences do not exceed 5∙10–4 for
and those presented in reference [3].
The differences do not exceed 5∙10–4 for ![]() and 3∙10–2 for
and 3∙10–2 for ![]() . Moreover, it can be shown that the
differences decrease as the number of annular membranes
. Moreover, it can be shown that the
differences decrease as the number of annular membranes ![]() is
increased.
is
increased.
The frequencies of the circular composite
membrane of radius ![]() consisting
of three parts (a circular inner membrane and two annular membranes) as
functions of the ratio
consisting
of three parts (a circular inner membrane and two annular membranes) as
functions of the ratio ![]() , are presented in Figure 2
for
, are presented in Figure 2
for ![]() The material density of the inner
annular membrane is much greater than the density of the other parts of the membrane, i.e.
The material density of the inner
annular membrane is much greater than the density of the other parts of the membrane, i.e. ![]() , and
, and ![]() . The calculations were performed for:
. The calculations were performed for: ![]() and
and ![]() Figure
2 shows that both the material density (or membrane thickness) and the location
of the inner annular membrane cause significant changes in the eigenfrequencies
of the composite membrane.
Figure
2 shows that both the material density (or membrane thickness) and the location
of the inner annular membrane cause significant changes in the eigenfrequencies
of the composite membrane.
Table 1
Values of ![]() for an annular membrane,
for an annular membrane,
![]()
![]()
|
|
a = 1.0 |
a = 2.0 |
||||||
|
m |
Ref [3] |
m |
Ref [3] |
|||||
|
10 |
15 |
20 |
10 |
15 |
20 |
|||
|
W01 |
3.0156 |
3.0156 |
3.0156 |
3.0156 |
2.5691 |
2.5691 |
2.5691 |
2.5691 |
|
W02 |
6.1639 |
6.1640 |
6.1640 |
6.1640 |
5.2653 |
5.2654 |
5.2654 |
5.2654 |
|
W03 |
9.2537 |
9.2937 |
9.2937 |
9.2937 |
7.9442 |
7.9442 |
7.9443 |
7.9443 |
|
W04 |
12.4161 |
12.4163 |
12.4163 |
12.4163 |
10.6161 |
10.6163 |
10.6164 |
10.6164 |
|
W05 |
15.5350 |
15.5354 |
15.5354 |
15.5354 |
13.2845 |
13.2851 |
13.2852 |
13.2852 |
|
W11 |
3.3349 |
3.3349 |
3.3349 |
3.3349 |
2.8360 |
2.8360 |
2.8360 |
2.8360 |
|
W12 |
6.3801 |
6.3801 |
6.3802 |
6.3802 |
5.4503 |
5.4504 |
5.4504 |
5.4504 |
|
W13 |
9.4532 |
9.4532 |
9.4532 |
9.4532 |
8.0825 |
8.0826 |
8.0826 |
8.0826 |
|
W14 |
12.5414 |
12.5415 |
12.5416 |
12.5416 |
10.7255 |
10.7258 |
10.7258 |
10.7259 |
|
W15 |
15.6377 |
15.6381 |
15.6381 |
15.6381 |
13.3746 |
13.3753 |
13.3753 |
13.3754 |
|
W21 |
4.0734 |
4.0734 |
4.0734 |
4.0734 |
3.4492 |
3.4492 |
3.4492 |
3.4492 |
|
W22 |
6.9718 |
6.9718 |
6.9718 |
6.9718 |
5.9526 |
5.9526 |
5.9526 |
5.9526 |
|
W23 |
9.9155 |
9.9156 |
9.9156 |
9.9156 |
8.4816 |
8.4817 |
8.4817 |
8.4817 |
|
W24 |
12.9120 |
12.9122 |
12.9122 |
12.9123 |
11.0488 |
11.0491 |
11.0492 |
11.0492 |
|
W25 |
15.9440 |
15.9444 |
15.9445 |
15.9445 |
13.6434 |
13.6441 |
13.6442 |
13.6443 |
|
W31 |
4.9359 |
4.9359 |
4.9359 |
4.9359 |
4.1603 |
4.1603 |
4.1603 |
4.1603 |
|
W32 |
7.7955 |
7.7956 |
7.7956 |
7.7956 |
6.6424 |
6.6424 |
6.6425 |
6.6425 |
|
W33 |
10.6269 |
10.6271 |
10.6271 |
10.6271 |
9.0889 |
9.0891 |
9.0892 |
9.0892 |
|
W34 |
13.5092 |
13.5095 |
13.5095 |
13.5096 |
11.5663 |
11.5668 |
11.5669 |
11.5669 |
|
W35 |
16.4474 |
16.4480 |
16.4481 |
16.4481 |
14.0838 |
14.0848 |
14.0850 |
14.0850 |
Table 2
Values of ![]() for a circular membrane,
for a circular membrane, ![]()
|
|
a = 1.0 |
a = 2.0 |
||||||
|
m |
Ref [3] |
m |
Ref [3] |
|||||
|
10 |
15 |
20 |
10 |
15 |
20 |
|||
|
W01 |
2.0108 |
2.0108 |
2.0108 |
2.0108 |
1.7598 |
1.7598 |
1.7598 |
1.7598 |
|
W02 |
4.5548 |
4.5549 |
4.5549 |
4.5549 |
3.9802 |
3.9802 |
3.9802 |
3.9802 |
|
W03 |
7.1194 |
7.1195 |
7.1196 |
7.1196 |
6.2147 |
6.2149 |
6.2150 |
6.2150 |
|
W04 |
9.6897 |
9.6900 |
9.6901 |
9.6901 |
8.4537 |
8.4542 |
8.4543 |
8.4543 |
|
W05 |
12.2622 |
12.2629 |
12.2631 |
12.2631 |
10.6943 |
10.6956 |
10.6957 |
10.6958 |
|
W11 |
3.0678 |
3.0678 |
3.0678 |
3.0678 |
2.6273 |
2.6273 |
2.6273 |
2.6273 |
|
W12 |
5.6990 |
5.6991 |
5.6991 |
5.6991 |
4.9267 |
4.9268 |
4.9268 |
4.9268 |
|
W13 |
8.3004 |
8.3006 |
8.3006 |
8.3006 |
7.1990 |
7.1993 |
7.1993 |
7.1994 |
|
W14 |
10.8914 |
10.8919 |
10.8920 |
10.8920 |
9.4608 |
9.4616 |
9.4617 |
9.4618 |
|
W15 |
13.4773 |
13.4785 |
13.4786 |
13.4787 |
11.7170 |
11.7188 |
11.7191 |
11.7192 |
|
W21 |
4.0223 |
4.0223 |
4.0224 |
4.0224 |
3.4110 |
3.4110 |
3.4110 |
3.4110 |
|
W22 |
6.7453 |
6.7454 |
6.7454 |
6.7454 |
5.7872 |
5.7874 |
5.7874 |
5.7874 |
|
W23 |
9.3940 |
9.3943 |
9.3944 |
9.3944 |
8.1011 |
8.1015 |
8.1016 |
8.1016 |
|
W24 |
12.0150 |
12.0157 |
12.0158 |
12.0159 |
10.3905 |
10.3916 |
10.3918 |
10.3919 |
|
W25 |
14.6217 |
14.6234 |
14.6236 |
14.6236 |
12.6665 |
12.6691 |
12.6694 |
12.6696 |
|
W31 |
4.9283 |
4.9283 |
4.9284 |
4.9284 |
4.1549 |
4.1549 |
4.1550 |
4.1550 |
|
W32 |
7.7381 |
7.7383 |
7.7383 |
7.7383 |
6.6029 |
6.6031 |
6.6032 |
6.6032 |
|
W33 |
10.4357 |
10.4362 |
10.4362 |
10.4363 |
8.9581 |
8.9587 |
8.9588 |
8.9588 |
|
W34 |
13.0894 |
13.0904 |
13.0906 |
13.0906 |
11.2758 |
11.2774 |
11.2776 |
11.2776 |
|
W35 |
15.7197 |
15.7220 |
15.7223 |
15.7224 |
13.5726 |
13.5763 |
13.5767 |
13.5768 |
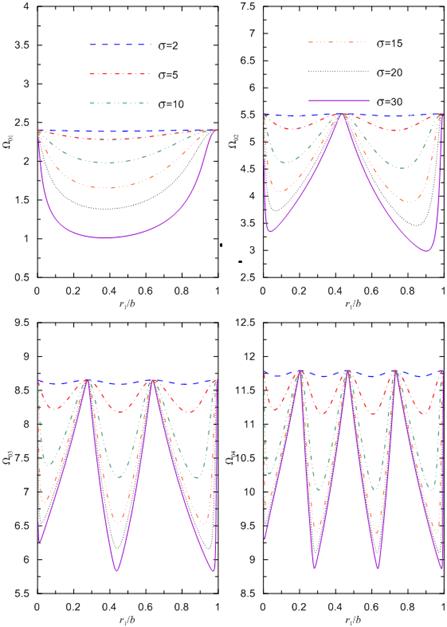
Fig. 2. Four free
vibration frequencies ![]() of the circular
composite membrane
consisting of three segments for n = 0, as functions of the ratio
of the circular
composite membrane
consisting of three segments for n = 0, as functions of the ratio ![]() for various
for various ![]() and
and ![]()
5. Conclusions
In this paper, a solution to the free vibration problem of annular and circular composite membranes has been derived. Numerical analysis has shown the effect of parameters characterizing the composite annular or circular membranes on their eigenfrequencies. The frequency analysis was performed for a circular membrane with an inner highlighted annular membrane whose material density (or thickness) is much greater than the material density (or thickness) of the remaining part of the membrane. The numerical results show that the location of the highlighted annular membrane has a significant effect on eigenfrequencies of the composite membrane. It follows that the application of this annular membrane can be used to introduce a specific change in the dynamical characteristic of the composite membrane. Numerical examples show that the presented method can be used to determine approximate natural frequencies of composite membranes with continuously varying densities or thicknesses.
References
[1] Laura P.A.A., Rossit C.A., La Malfa S., Transverse vibrations of composite, circular annular membranes: exact solution, Journal of Sound and Vibration 1998, 216(1), 190-193.
[2] Gottlieb H.P.W., Exact solutions for vibrations of some annular membranes with inhomogeneous radial densities, Journal of Sound and Vibration 2000, 223(1), 165-170.
[3] Jabareen M., Eisenberger M., Free vibrations of non-homogeneous circular and annular membranes, Journal of Sound and Vibration 2001, 240(3), 409-429.
[4] Cap F.F., Eigenfrequencies of membranes of arbitrary boundary and with varying surface mass density, Applied Mathematics and Computation 2001, 124, 319-329.
[5] Gutierrez A.A., Laura P.A.A., Bambill D.V., Jederlinic V.A., Hodges D.H., Axisymmetric vibrations of solid circular and annular membranes with continuously varying density, Journal of Sound and Vibration 1998, 212(4), 611-622.
[6] Wei-Peng H., Zi-Chen D., Wen-Cheng L., Multi-symplectic methods for membrane free vibration equation, Applied Mathematics and Mechanics 2007, 28(9), 1181-1189.
[7] Civalek Ö., Gürses M., Discrete singular convolution for free vibration analysis annular membranes, Mathematical and Computational Applications 2009, 14(2), 131-138.
[8] Reutskiy S.Y., The methods of external and internal excitation for problems of free vibrations of non-homogeneous membranes, Engineering Analysis with Boundary Elements 2007, 31, 906-918.
[9] Buchanan G.R., Vibration of circular membranes with linearly varying density along a diameter, Journal of Sound and Vibration 2005, 280, 407-414.
[10] Zamorska I., Kukla S., Siedlecka U., Frequency analysis of composite annular membranes, Scientific Research of the Institute of Mathematics and Computer Science 2012, 11(1), 129-135.
[11] Dahlquist G., Björck A., Numerical Methods in Scientific Computing, Society for Industrial and Applied Mathematics, Philadelphia 2008.

