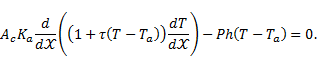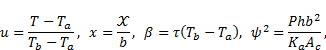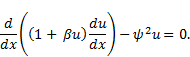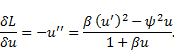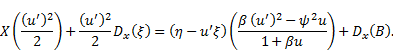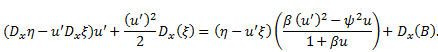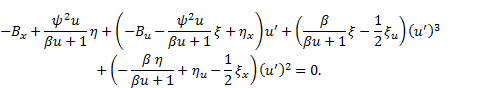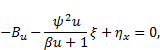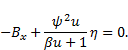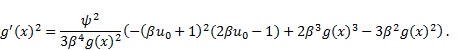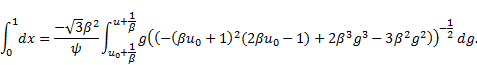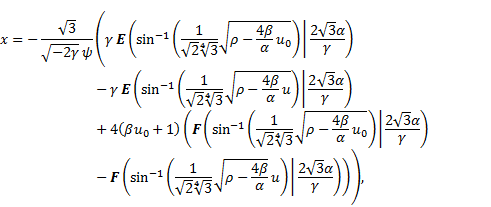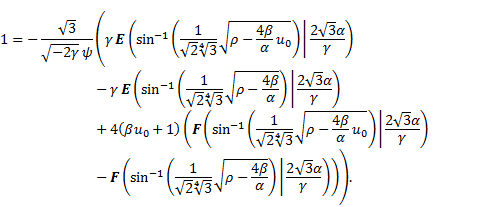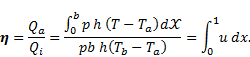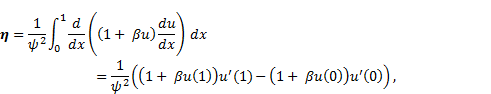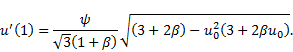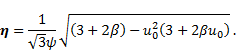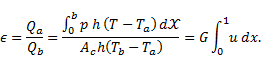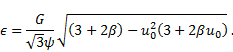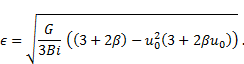EXACT SOLUTION OF FIN PROBLEM WITH LINEAR TEMPERATURE-DEPENDENT THERMAL CONDUCTIVITY
A.H. Abdel Kader, M.S. Abdel Latif, H.M.
Nour
Mathematics and Engineering Physics
Department, Faculty of Engineering
Mansoura University, Egypt
Leaderabass87@gmail.com, m_gazia@mans.edu.eg, hanour@mans.edu.eg
Received: 20
September 2016; accepted: 15 November 2016
Abstract: In
this paper, we obtain the general exact solution of a nonlinear fin equation
which governs heat transfer in a rectangular fin with linear
temperature-dependent thermal conductivity using the partial
Noether method. The
relationship between the fin efficiency and the
thermo-geometric fin parameter is obtained. Additionally, we obtained the relationship among the fin effectiveness,
the thermo-geometric fin parameter and the Biot number.
Keywords: exact solution, fin
equation, fin efficiency, thermal conductivity
1. Introduction
In this paper, we
assume that the rectangular fin subjected to some assumptions such as steady
state heat transfer operation with no heat generation, the fin tip
is insulated, and the heat transfer is one dimensional. Under these
assumptions,
the energy balance equation of rectangular fin is given by [1-11]
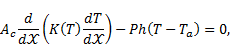 | (1) |
where, 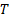 is the fin temperature,
is the fin temperature, 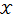 is the axial distance
measured from the fin tip,
is the axial distance
measured from the fin tip, 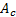 is the cross-sectional
area of the fin,
is the cross-sectional
area of the fin, 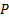 is the fin
perimeter,
is the fin
perimeter,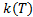 is the thermal
conductivity of the fin,
is the thermal
conductivity of the fin, 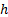 is the heat transfer
coefficient and
is the heat transfer
coefficient and 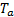 is the ambient
temperature.
is the ambient
temperature.
Here, we take the
heat transfer coefficient 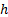 as a
constant and the thermal conductivity
as a
constant and the thermal conductivity 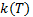 as a linear function
of temperature [1-9]
as a linear function
of temperature [1-9]
where 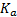 is the thermal
conductivity of the fin at the ambient temperature
is the thermal
conductivity of the fin at the ambient temperature 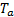 ,
,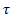 is
a constant.
is
a constant.
Substituting (2) into (1), we obtain
To make Eq. (3) dimensionless; the following
transformations are introduced
[1-14]
where, 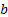 is the length of fin,
is the length of fin, 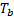 is the temperature of the heat source where
the fin is attached and the parameter
is the temperature of the heat source where
the fin is attached and the parameter 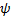 is called thermo geometric fin parameter.
is called thermo geometric fin parameter.
Using the transformations (4), Eq. (3) becomes
Equation (5) can be rewritten as
The boundary
conditions are:
At the fin tip 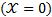 , since the fin tip is
insulated, so
, since the fin tip is
insulated, so
Using the transformation (4), Eq. (7) becomes
At the fin base 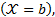 the fin temperature is
the same temperature as the heat source
the fin temperature is
the same temperature as the heat source 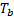
Using the transformation (4), Eq. (9) becomes
Approximate solutions of Eq. (6) with
boundary conditions (8) and (10) are
investigated using the Parameterized Perturbation
method in [1], by using optimal homotopy asymptotic method in [2], by using the
homotopy analysis method
in [3, 4], by using the Residue minimization technique in [5], by using
the variational iteration method in [6] and by using the decomposition method
in [7, 8].
The homotopy analysis method is widely used in investigating many fin problems
in [12-14]. In this paper, we will obtain the exact solution of Eq. (6) using
the partial Noether method.
The paper will be organized as follows: In
section 2, the exact solution of
Eq. (6) is obtained using the partial Noether method. In section 3, the fin
efficiency will be discussed. In section 4, the fin effectiveness is studied.
In section 5, we will discuss the obtained results in this paper.
2. Partial Noether Method
Definition [15, 16]. A Lie operator 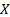 of a form
of a form
is called a partial Noether operator
corresponding to a partial Lagrangian 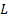 , if there exists
a function
, if there exists
a function 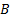 , such that
, such that
where 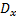 is the total differentiation with respect to
is the total differentiation with respect to 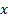 and
and 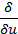 is called the Euler-
-Lagrange operator, which are defined as,
is called the Euler-
-Lagrange operator, which are defined as,
Theorem [15, 16]. If the Lie operator (11) is a partial Noether operator corresponding
to a partial Lagrangian 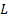 of Eq. (6), then the
first integral
of Eq. (6), then the
first integral 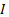 of (6) is
given by
of (6) is
given by
which is satisfied by the conservation law
where, 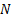 is a Noether operator
which is defined as:
is a Noether operator
which is defined as:
where,
Consider the partial Lagrangian of Equation (6)
[15, 16]
where,
To obtain the partial Noether operator of Eq.
(6), we will substitute (18) and (19) into the condition (12) to obtain
Substituting (11) into (20), we obtain the
determining equation
Let,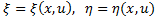 and
and 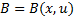 , the determining equation (21) becomes
, the determining equation (21) becomes
Equating the coefficients of the derivatives of 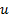 with zero, we obtain
with zero, we obtain
The solution of system (23)-(26) is given by
Substituting (18) into (16), we obtain
Substituting (27) and (28) into (14), we obtain
Suppose the first integral 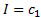 , hence, we obtain
, hence, we obtain
where 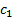 is a constant. Using
the boundary condition (8), we can determine
the constant
is a constant. Using
the boundary condition (8), we can determine
the constant 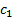 as follows
as follows
where, 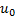 is the temperature of
fin at the fin tip
is the temperature of
fin at the fin tip 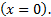 Substituting (31) into
(30), we obtain
Substituting (31) into
(30), we obtain
Let,
Hence, Eq. (32) becomes
Integrating Eq. (33), we obtain
Hence, we obtain the following exact implicit
solution of Eq. (5)
where, 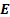 is the
incomplete elliptic integral of the second kind, which is defined as [17]
is the
incomplete elliptic integral of the second kind, which is defined as [17]
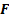 is the incomplete elliptic integral of the first kind, which is defined as
[17]
is the incomplete elliptic integral of the first kind, which is defined as
[17]
and 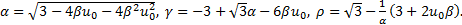
The solution (35) has an unknown parameter
namely 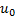 . This parameter can be
easily determined with the help of the boundary condition
. This parameter can be
easily determined with the help of the boundary condition 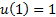 as follows:
as follows:
Equation (36) shows the relation between the
temperature at fin tip 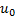 and the
thermo-geometric parameter
and the
thermo-geometric parameter 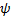 and
and 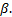
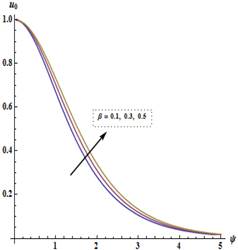
Figure 1 shows the effect of the
thermo-geometric parameter 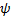 on the fin tip
temperature
on the fin tip
temperature 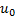 . We find that the fin
tip temperature
. We find that the fin
tip temperature 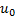 decreases with
increasing
decreases with
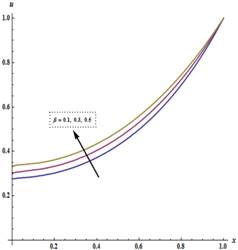
increasing 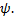 Figure 2 shows the distribution of fin temperature
Figure 2 shows the distribution of fin temperature 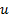 along the fin. We find that
the fin temperature decreases with increasing
along the fin. We find that
the fin temperature decreases with increasing 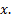
3. Fin efficiency
The fin efficiency
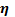 is the ratio of the
actual heat transfer rate
is the ratio of the
actual heat transfer rate 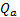 from the fin to ideal
heat transfer
from the fin to ideal
heat transfer 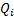 rate from the fin if
the entire fin were at base temperature
[3-11]
rate from the fin if
the entire fin were at base temperature
[3-11]
Using Eq. (5), Eq. (37) becomes
Using the boundary conditions (8) and (10), Eq. (38)
becomes
From (32), when 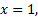 we obtain
we obtain
Substituting (40) into (39), we obtain
Using the relations (41) and (36), we can plot
the relation between the efficiency 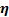 and the thermo-geometric fin parameter
and the thermo-geometric fin parameter 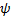 (see Figure 3).
(see Figure 3).
3. Fin effectiveness
Fin effectiveness ϵ is the ratio of
heat transferred from the fin area 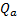 to the heat which
would be transferred if entire fin area was at base temperature
to the heat which
would be transferred if entire fin area was at base temperature 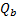 [11]
[11]
where, 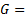
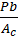 is a parameter
which depends on the fin geometry.
is a parameter
which depends on the fin geometry.
From (37), we find
Substituting (41) into (43), we obtain
The parameter 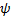 can be rewritten in the form
can be rewritten in the form
where, 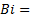
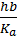 is the Biot number.
is the Biot number.
Substituting (45) into (44), we obtain
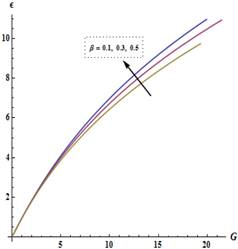
Using the relations (45), (46) and (36), we
can plot the relation between the fin effectiveness 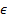 and the parameters
and the parameters 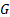 and
and 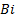 (Figures 4
and 5).
(Figures 4
and 5).
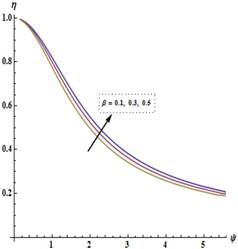
Figure 3 shows the effect of the
thermo-geometric parameter 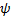 on fin efficiency
on fin efficiency 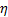 . We find that the fin efficiency
. We find that the fin efficiency 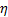 decreases with increasing
decreases with increasing 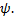 Figure 4 shows
the effect of the parameter
Figure 4 shows
the effect of the parameter 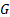 on fin effectiveness
on fin effectiveness 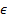 . We find that fin effectiveness
. We find that fin effectiveness 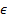 increases with increasing
increases with increasing 
Fig. 5. Plot the
relation between the fin effectiveness 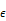 and
and 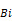 when
when 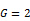 for various values of
for various values of 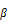
Figure 5 shows the effect of the Biot number on
fin effectiveness 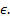 We find that
fin effectiveness
We find that
fin effectiveness 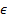 decreases with increasing
decreases with increasing 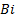 .
.
5. Discussions and concluding remarks
In this paper, we obtain the general exact
solution (35) of the fin equation (5) which is subjected to the boundary
conditions (8) and (10). The solution is valid for all values of the thermo-geometric
fin parameters 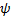 and
and 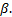 We observe in Figure 1 that the fin tip temperature
We observe in Figure 1 that the fin tip temperature 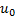 decreases with an
increase in the thermo-geometric parameter
decreases with an
increase in the thermo-geometric parameter 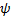 . Figure 2 shows that
the fin temperature
. Figure 2 shows that
the fin temperature 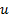 increases with an
increasing
increases with an
increasing 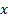 (in other words, the temperature increases when approaching a heat source). The
relation between the fin efficiency
(in other words, the temperature increases when approaching a heat source). The
relation between the fin efficiency 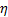 and the parameters
and the parameters 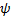 and
and 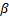 is obtained.
Figure 3 shows that the fin efficiency
is obtained.
Figure 3 shows that the fin efficiency 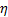 decreases with
increasing the thermo-geo-
metric parameter
decreases with
increasing the thermo-geo-
metric parameter 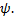 The relation between the fin effectiveness
The relation between the fin effectiveness 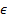 and the parameters,
and the parameters, 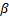 and Biot number
and Biot number 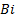 is obtained. Figures 4 and 5 show that the fin effectiveness
is obtained. Figures 4 and 5 show that the fin effectiveness 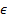 increases when increasing
increases when increasing 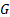 and decreases when increasing the Biot number
and decreases when increasing the Biot number 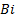 .
.
References
[1]
Seiyed Ghasemi E., Ali Zolfagharian, M. Hatam,
Ganji D.D., Analytical thermal study on nonlinear
fundamental heat transfer cases using a novel computational technique, Applied
Thermal Engineering 2016, 98, 88-97.
[2]
Saeed Dinarvand, Reza Hosseini, Optimal homotopy
asymptotic method for convective-radiative cooling of a lumped system, and
convective straight fin with temperature-dependent thermal conductivity, Afr.
Mat. 2013, 24, 103-116.
[3]
Srikumar Panda, A study on nonlinear wet fin
problem using homotopy analysis method,
Int. J. Appl. Comput. Math, 2016, DOI: 10.1007/s40819-016-0188-1.
[4]
Mustafa Inc: Application of homotopy analysis
method for fin efficiency of convective straight fins with
temperature-dependent thermal conductivity, Mathematics and Computers in
Simulation 2008, 79, 189-200.
[5]
Kulkarni D.B., Joglekar M.M., Residue
minimization technique to analyze the efficiency
of convective straight fins having temperature-dependent thermal
conductivity, Applied Mathematics and Computation 2009, 215, 2184-2191.
[6]
Safa Bozkurt Coskun, Mehmet Tarik Atay, Fin efficiency analysis of convective straight fins with temperature
dependent thermal conductivity using variational iteration method, Applied
Thermal Engineering 2008, 28, 2345-2352.
[7]
Cihat Arslanturk, A decomposition method for fin
efficiency of convective straight fins with temperature-dependent thermal
conductivity, International Communications in Heat and Mass Transfer 2005, 32,
831-841.
[8]
Ching-Huang Chiu, Cha’o-Kuang Chen, A
decomposition method for solving the convective longitudinal fins with
variable thermal conductivity, Int. J. Heat and Mass Transfer. 2002, 45,
2067-2075.
[9]
Abdel Latif M.S., Abdel Kader A.H., Nour H.M., Exact implicit solution of nonlinear heat transfer in rectangular
straight fin using symmetry reduction methods, Appl. Appl. Math. 2015, 10, 2,
864-877.
[10] Abdel Kader A.H., Abdel
Latif M.S., Nour H.M., General exact solution of the fin problem
with variable thermal conductivity, Propulsion and
Power Research 2016, 5(1), 63-69.
[11] Abdel Kader A.H., Abdel
Latif M.S., Nour H.M., General exact solution of the fin problem
with the power law temperature - dependent thermal conductivity, Math. Meth. Appl. Sci. 2016, 39, 1513-1521.
[12] Srikumar Panda, Arka Bhowmik, Ranjan Das, Ramjee Repaka, Subash S.C.
Martha, Application of homotopy analysis method and inverse solution of a
rectangular wet fin, Energy Conversion and Management 2014, 80, 305-318.
[13] Arka Bhowmik,
Srikumar Panda, Ranjan Das, Ramjee Repaka, Subash S.C. Martha, Inverse analysis
of conductive-convective wet triangular fin for predicting thermal properties
and fin dimensions, Inverse Problems in Science and Engineering 2014, 22(8),
1367-1393.
[14] Srikumar Panda, Arka Bhowmik, Homotopy analysis method for thermal
analysis of wet
fin with all nonlinearity, International Conference on Engineering (NUiCONE),
2013, 1-6, DOI:10.1109/NUiCONE.2013. 6780197.
[15] Kara A.H., Mahomed F.M., Naeem I., Wafo Soh C., Partial Noether
operators and first integrals via partial Lagrangians, Math. Meth. Appl. Sci.
2007, 30, 2079-2089.
[16] Naeem I., Mahomed F.M., Noether, partial Noether operators and first
integrals for a linear
system, J. Math. Anal. Appl. 2008, 342, 70-82.
[17] Frank Olver W.J., Lozier D.W., Boisvert R.F., Clark C.W., Nist
Handbook of Mathematical Functions 2010.



![]() is the fin temperature,
is the fin temperature, ![]() is the axial distance
measured from the fin tip,
is the axial distance
measured from the fin tip, ![]() is the cross-sectional
area of the fin,
is the cross-sectional
area of the fin, ![]() is the fin
perimeter,
is the fin
perimeter,![]() is the thermal
conductivity of the fin,
is the thermal
conductivity of the fin, ![]() is the heat transfer
coefficient and
is the heat transfer
coefficient and ![]() is the ambient
temperature.
is the ambient
temperature.![]() as a
constant and the thermal conductivity
as a
constant and the thermal conductivity ![]() as a linear function
of temperature [1-9]
as a linear function
of temperature [1-9]![]() is the thermal
conductivity of the fin at the ambient temperature
is the thermal
conductivity of the fin at the ambient temperature ![]() ,
,![]() is
a constant.
is
a constant.![]() is the length of fin,
is the length of fin, ![]() is the temperature of the heat source where
the fin is attached and the parameter
is the temperature of the heat source where
the fin is attached and the parameter ![]() is called thermo geometric fin parameter.
is called thermo geometric fin parameter.![]() , since the fin tip is
insulated, so
, since the fin tip is
insulated, so![]() the fin temperature is
the same temperature as the heat source
the fin temperature is
the same temperature as the heat source ![]()
![]() of a form
of a form![]() , if there exists
a function
, if there exists
a function ![]() , such that
, such that![]() is the total differentiation with respect to
is the total differentiation with respect to ![]() and
and ![]() is called the Euler-
-Lagrange operator, which are defined as,
is called the Euler-
-Lagrange operator, which are defined as,![]() of Eq. (6), then the
first integral
of Eq. (6), then the
first integral ![]() of (6) is
given by
of (6) is
given by![]() is a Noether operator
which is defined as:
is a Noether operator
which is defined as:![]() and
and ![]() , the determining equation (21) becomes
, the determining equation (21) becomes![]() with zero, we obtain
with zero, we obtain![]() , hence, we obtain
, hence, we obtain![]() is a constant. Using
the boundary condition (8), we can determine
the constant
is a constant. Using
the boundary condition (8), we can determine
the constant ![]() as follows
as follows![]() is the temperature of
fin at the fin tip
is the temperature of
fin at the fin tip ![]() Substituting (31) into
(30), we obtain
Substituting (31) into
(30), we obtain![]() is the
incomplete elliptic integral of the second kind, which is defined as [17]
is the
incomplete elliptic integral of the second kind, which is defined as [17]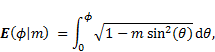
![]() is the incomplete elliptic integral of the first kind, which is defined as
[17]
is the incomplete elliptic integral of the first kind, which is defined as
[17]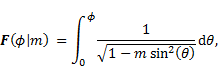
![]()
![]() . This parameter can be
easily determined with the help of the boundary condition
. This parameter can be
easily determined with the help of the boundary condition ![]() as follows:
as follows:![]() and the
thermo-geometric parameter
and the
thermo-geometric parameter ![]() and
and ![]()
![]() on the fin tip
temperature
on the fin tip
temperature ![]() . We find that the fin
tip temperature
. We find that the fin
tip temperature ![]() decreases with
increasing
decreases with
increasing ![]() Figure 2 shows the distribution of fin temperature
Figure 2 shows the distribution of fin temperature ![]() along the fin. We find that
the fin temperature decreases with increasing
along the fin. We find that
the fin temperature decreases with increasing ![]()
![]() is the ratio of the
actual heat transfer rate
is the ratio of the
actual heat transfer rate ![]() from the fin to ideal
heat transfer
from the fin to ideal
heat transfer ![]() rate from the fin if
the entire fin were at base temperature
[3-11]
rate from the fin if
the entire fin were at base temperature
[3-11] ![]() we obtain
we obtain![]() and the thermo-geometric fin parameter
and the thermo-geometric fin parameter ![]() (see Figure 3).
(see Figure 3).![]() to the heat which
would be transferred if entire fin area was at base temperature
to the heat which
would be transferred if entire fin area was at base temperature ![]() [11]
[11]![]()
![]() is a parameter
which depends on the fin geometry.
is a parameter
which depends on the fin geometry.![]() can be rewritten in the form
can be rewritten in the form![]()
![]() is the Biot number.
is the Biot number.![]() and the parameters
and the parameters ![]() and
and ![]() (Figures 4
and 5).
(Figures 4
and 5).![]() on fin efficiency
on fin efficiency ![]() . We find that the fin efficiency
. We find that the fin efficiency ![]() decreases with increasing
decreases with increasing ![]() Figure 4 shows
the effect of the parameter
Figure 4 shows
the effect of the parameter ![]() on fin effectiveness
on fin effectiveness ![]() . We find that fin effectiveness
. We find that fin effectiveness ![]() increases with increasing
increases with increasing ![]()

![]() and
and ![]() when
when ![]() for various values of
for various values of ![]()
![]() We find that
fin effectiveness
We find that
fin effectiveness ![]() decreases with increasing
decreases with increasing ![]() .
.![]() and
and ![]() We observe in Figure 1 that the fin tip temperature
We observe in Figure 1 that the fin tip temperature ![]() decreases with an
increase in the thermo-geometric parameter
decreases with an
increase in the thermo-geometric parameter ![]() . Figure 2 shows that
the fin temperature
. Figure 2 shows that
the fin temperature ![]() increases with an
increasing
increases with an
increasing ![]() (in other words, the temperature increases when approaching a heat source). The
relation between the fin efficiency
(in other words, the temperature increases when approaching a heat source). The
relation between the fin efficiency ![]() and the parameters
and the parameters ![]() and
and ![]() is obtained.
Figure 3 shows that the fin efficiency
is obtained.
Figure 3 shows that the fin efficiency ![]() decreases with
increasing the thermo-geo-
metric parameter
decreases with
increasing the thermo-geo-
metric parameter ![]() The relation between the fin effectiveness
The relation between the fin effectiveness ![]() and the parameters,
and the parameters, ![]() and Biot number
and Biot number ![]() is obtained. Figures 4 and 5 show that the fin effectiveness
is obtained. Figures 4 and 5 show that the fin effectiveness ![]() increases when increasing
increases when increasing ![]() and decreases when increasing the Biot number
and decreases when increasing the Biot number ![]() .
.