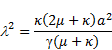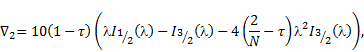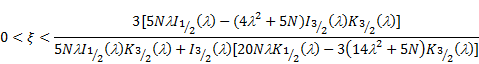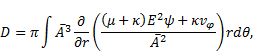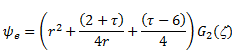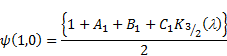Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations
Vandana Mishra
,Bali Ram Gupta
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Mishra_2016,
doi = {10.17512/jamcm.2016.3.10},
url = {https://doi.org/10.17512/jamcm.2016.3.10},
year = 2016,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {15},
number = {3},
pages = {97--109},
author = {Vandana Mishra and Bali Ram Gupta},
title = {Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2016.3.10 UR - https://doi.org/10.17512/jamcm.2016.3.10 TI - Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Mishra, Vandana AU - Gupta, Bali Ram PY - 2016 PB - The Publishing Office of Czestochowa University of Technology SP - 97 EP - 109 IS - 3 VL - 15 SN - 2299-9965 SN - 2353-0588 ER -
Mishra, V., & Gupta, B. (2016). Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations. Journal of Applied Mathematics and Computational Mechanics, 15(3), 97-109. doi:10.17512/jamcm.2016.3.10
Mishra, V. & Gupta, B., 2016. Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations. Journal of Applied Mathematics and Computational Mechanics, 15(3), pp.97-109. Available at: https://doi.org/10.17512/jamcm.2016.3.10
[1]V. Mishra and B. Gupta, "Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 3, pp. 97-109, 2016.
Mishra, Vandana, and Bali Ram Gupta. "Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations." Journal of Applied Mathematics and Computational Mechanics 15.3 (2016): 97-109. CrossRef. Web.
1. Mishra V, Gupta B. Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(3):97-109. Available from: https://doi.org/10.17512/jamcm.2016.3.10
Mishra, Vandana, and Bali Ram Gupta. "Drag on a permeable sphere placed in a micropolar fluid with non-zero boundary condition for microrotations." Journal of Applied Mathematics and Computational Mechanics 15, no. 3 (2016): 97-109. doi:10.17512/jamcm.2016.3.10
DRAG ON A PERMEABLE SPHERE PLACED IN A MICROPOLAR FLUID WITH NON-ZERO BOUNDARY CONDITION FOR MICROROTATIONS
Vandana Mishra, Bali Ram Gupta
Department of Mathematics, Jaypee
University of Engineering & Technology
Guna, M.P, India
mishrav635@gmail.com, baliram.gupta@juet.ac.in
Abstract. This paper concerns an analytical study of an infinite expanse of uniform flow of steady axisymmetric creeping flow of an incompressible micropolar fluid around the permeable sphere assuming a nonhomogeneous boundary condition for microrotation vector. It is assumed that microrotation vector is proportional to the rotation rate of velocity vector. The stream function solutions for the flow fields are obtained in the terms of modified Bessel’s functions and Gegenbauer functions. Continuity of normal velocity, no-slip condition, non-zero microrotation vector on the sphere, uniform velocity at infinity are the different boundary conditions used to determine the flow fields explicitly. The micro- rotation component, pressure field, bounds of permeability parameter and drag force experienced by the permeable sphere are calculated. Dependence of the drag force on different fluid parameters is presented graphically and discussed. It is found that drag force decreases with increasing spin parameter. Several cases of interest are deduced from the present analysis.
Keywords: drag force, modified Bessel’s function, micropolar fluid, permeable sphere, stream function
1. Introduction
The investigation of viscous flow through permeable media has fascinated substantial practical and theoretical interest in science, designing and innovation. In our day to day life, we observe that the permeable objects and permeability nature correspond to various types of viscous and non viscous fluids passing through the objects viz. cloth, sand, paper etc. Many different theoretical and experimental models have been proposed, which explain the viscous flow past and within porous bodies. Some more examples of such flow are a flow past a meshed spherical surface, soil etc.
Darcy [1] proposed the initial study of the fluid flow in a permeable medium and stated that the flow rate in porous media is proportional to the pressure gradient. Many different approaches [2-4] implemented to explain the creeping flow of an incompressible viscous fluid about permeable sphere. Joseph and Tao [5] investi- gated that the slow motion of a viscous fluid past a permeable sphere in an uniform stream can be calculated in an analogous analytic form if the fluid in the permeable sphere obeys the Darcy’s law. Birikh and Rudakoh [6] investigated the problem of slow motion of a permeable sphere in a viscous fluid and evaluated the drag and the flow rate of the fluid. Padmavathi et al. [8] solved the problem of stokes flow past a permeable sphere for the non-axisymmetric case and gave a general method for calculating non-axisymmetric flow both outside and inside the permeable spherical boundary and expressions for drag and torque on the sphere. Usha [9] solved the problem of creeping flow over concentric permeable spheres in relative motion. The problem on slow viscous flow past a spinning sphere with permeable surface was solved by Vasudeviah and Malathi [10], and they derived the expression for drag coefficient on the body which can be used as a formula for the determination of the permeability of the sphere.
Eringer [11]
introduced a subclass of viscous fluids, which he named micro-
polar fluids, that ignores the deformation of the microelement but still allows
for the particle micromotion to take place. Apart from the classical field of
velocity,
in the micropolar fluid theory there are
two additional field variables, viz. the micro-
rotation vector ![]() and the gyration
parameter
and the gyration
parameter![]() ; introduced to explain
the kinematic of microrotation. Ramkisoon and
Majumdar [12] derived a formula to evaluate drag on axially symmetric
bodies for the case of micropolar fluid and they
observed that the drag in the micropolar fluid is greater than that in the
classical fluid. The slow stationary flow of a micropolar fluid past a sphere
was studied
by Rao and Rao [13]. Srinivasacharya and Rajyalakshmi [14] solved the problem
of the creeping flow of micropolar fluid past a porous sphere and observed that
the drag on the porous sphere, when the fluid is micropolar, is more than that
of
the Newtonian fluid. Ramkissoon [15] has obtained the solution for the problem
of a micropolar fluid flow around a Newtonian fluid sphere and evaluated the
drag force exerted on the sphere. The resistance force exerted on a solid
sphere moving with constant velocity in micropolar fluid with a non-homogeneous
boundary
condition for microrotation vector was tackled by Haffmann et al. [16]. Gupta
and Deo [17] have studied Stokes flow of micropolar fluid past a porous sphere
with non-zero boundary condition for microrotations. Drag on Reiner-Rivlin
liquid sphere placed in a micropolar fluid with non-zero boundary condition for
micro-
rotation has been solved by Jaiswal and Gupta [18]. Gupta and Deo [19] have
solved the problem of axisymmetric creeping flow of micropolar fluid over
a sphere coated with a thin fluid film. It is found that a sphere without
coating
experiences greater resistance in comparison to coated fluid. Slow steady
rotation of a permeable sphere in an incompressible couple stress fluid is
considered
by Aparna and Murthy [20] and they also studied the problem on uniform flow
of an incompressible micropolar fluid past a permeable sphere [21].
; introduced to explain
the kinematic of microrotation. Ramkisoon and
Majumdar [12] derived a formula to evaluate drag on axially symmetric
bodies for the case of micropolar fluid and they
observed that the drag in the micropolar fluid is greater than that in the
classical fluid. The slow stationary flow of a micropolar fluid past a sphere
was studied
by Rao and Rao [13]. Srinivasacharya and Rajyalakshmi [14] solved the problem
of the creeping flow of micropolar fluid past a porous sphere and observed that
the drag on the porous sphere, when the fluid is micropolar, is more than that
of
the Newtonian fluid. Ramkissoon [15] has obtained the solution for the problem
of a micropolar fluid flow around a Newtonian fluid sphere and evaluated the
drag force exerted on the sphere. The resistance force exerted on a solid
sphere moving with constant velocity in micropolar fluid with a non-homogeneous
boundary
condition for microrotation vector was tackled by Haffmann et al. [16]. Gupta
and Deo [17] have studied Stokes flow of micropolar fluid past a porous sphere
with non-zero boundary condition for microrotations. Drag on Reiner-Rivlin
liquid sphere placed in a micropolar fluid with non-zero boundary condition for
micro-
rotation has been solved by Jaiswal and Gupta [18]. Gupta and Deo [19] have
solved the problem of axisymmetric creeping flow of micropolar fluid over
a sphere coated with a thin fluid film. It is found that a sphere without
coating
experiences greater resistance in comparison to coated fluid. Slow steady
rotation of a permeable sphere in an incompressible couple stress fluid is
considered
by Aparna and Murthy [20] and they also studied the problem on uniform flow
of an incompressible micropolar fluid past a permeable sphere [21].
The aim of this paper is to extend the work
of Aparna and Murthy [21] by
assuming a non-zero boundary condition instead
of zero boundary condition for microrotation
vector![]() The microrotation on the boundary of
the sphere is assumed to be proportional to the rotational rate of the velocity
field on the boundary.
The stream function and pressure for the flow outside and inside of the sphere
are calculated. The drag experienced by a permeable sphere is evaluated and
the graphical representation of the drag force with respect to the different
fluid
parameters is displayed. The effect of fluid parameters on velocities and
stream functions are discussed.
The microrotation on the boundary of
the sphere is assumed to be proportional to the rotational rate of the velocity
field on the boundary.
The stream function and pressure for the flow outside and inside of the sphere
are calculated. The drag experienced by a permeable sphere is evaluated and
the graphical representation of the drag force with respect to the different
fluid
parameters is displayed. The effect of fluid parameters on velocities and
stream functions are discussed.
2. Mathematical formulas
Here we have considered a permeable sphere
of radius ![]() in an unbounded
medium with the origin at the centre
in an unbounded
medium with the origin at the centre ![]() of the sphere (Fig. 1). We assume that
the permeable sphere is stationary and a steady axisymmetric creeping flow of
a micropolar fluid has been established around it by a uniform flow with velocity
of magnitude
of the sphere (Fig. 1). We assume that
the permeable sphere is stationary and a steady axisymmetric creeping flow of
a micropolar fluid has been established around it by a uniform flow with velocity
of magnitude ![]() directed along the
directed along the ![]() -axis far away from the sphere.
-axis far away from the sphere.

Fig. 1. Graphical representation of the model
The general form of governing equations for the slow steady motion of micro- polar fluid under stokes approximation can be written as
| (1) |
| (2) |
| (3) |
where ![]() being the velocity vector,
being the velocity vector, ![]() the pressure,
the pressure, ![]() the microrotation
the microrotation
vector, ![]() the classical viscosity coefficient of the fluid,
the classical viscosity coefficient of the fluid, ![]() the
vortex viscosity
coefficients,
the
vortex viscosity
coefficients, ![]() are gyro viscosity coefficients satisfying the following
inequalities
are gyro viscosity coefficients satisfying the following
inequalities
| (4) |
To non-dimensionalize the equations and variables, we put
|
|
|
and drop tildes subsequently in further
analysis. Since the flow field is axisymmetric, we can introduce stream
functions ![]() which is related to
the velocity in spherical coordinate system
which is related to
the velocity in spherical coordinate system ![]() by Happel
and Brenner [7]
by Happel
and Brenner [7]
|
|
|
and we obtain two velocity components of the flow as
|
|
|
Eliminating the pressure from equation (2) and using (3) we get the differential equation
| (8) |
|
|
where , ![]() and micropolar parameter
and micropolar parameter
|
|
Using the equation (3) we get the micro-rotation component
|
|
|
3. Method of solution
The solution of Eq. (8) can be obtained by superimposing the solution of
| (11) |
in the form,
| (12) |
Suppose ![]() and
and ![]() denote the stream function solution for the external flow
(
denote the stream function solution for the external flow
(![]() ) and for the internal flow (
) and for the internal flow (![]() ) respectively. Using the method of separation of variables, the
stream function solution for external flow and internal flow are obtained as
) respectively. Using the method of separation of variables, the
stream function solution for external flow and internal flow are obtained as
|
|
|
and
| (14) |
where ![]() are modified Bessel functions of the first and second kind and
are modified Bessel functions of the first and second kind and ![]() is Gegenbauer polynomial.
is Gegenbauer polynomial.
The micro-rotation components ![]() and
and ![]() for external and internal flow are
for external and internal flow are
|
|
|
||||
|
|
|
4. Boundary conditions
The boundary conditions to be satisfied at the surface of the permeable sphere, which are physically realistic and mathematically consistent for this proposed problem, can be taken as:
· Continuity of normal velocity on the boundary i.e.
|
|
|
· No-slip condition across the surface i.e.
|
|
|
· The micro-rotation vector on the boundary is assumed to be proportional to the rotation rate of velocity which provides
|
|
|
· The condition at infinity for uniform stream as
|
|
|
· The pressure difference across the permeable boundary obeys Darcy’s law i.e.
|
|
|
where ![]() is the permeability ceofficient coefficient of the surface.
is the permeability ceofficient coefficient of the surface.
4.1. Determination of arbitrary constant
By applying the above boundary conditions (17)-(20) we obtain the following linear equations:
|
|
The above five linear equations involve six
arbitrary constants. Consequently, the unknown constants ![]() and
and ![]() are expressed in terms of
are expressed in terms of ![]() On solving above equations, we get
On solving above equations, we get
|
|
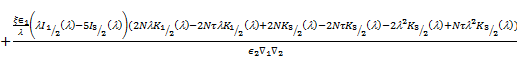 |
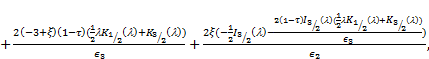 |
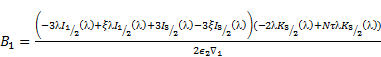 |
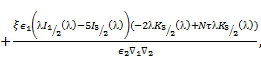 |
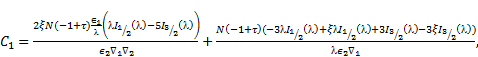 |
Where
|
We considered ![]() as the measure of permeability of the boundary surface which
reduces the uncertainty in the equation. In the case of
as the measure of permeability of the boundary surface which
reduces the uncertainty in the equation. In the case of ![]() the stream function for the internal region vanishes identically and
this corresponds to the case of an impermeable boundary. Here, we take the
problem of permeable sphere
for non-zero
the stream function for the internal region vanishes identically and
this corresponds to the case of an impermeable boundary. Here, we take the
problem of permeable sphere
for non-zero ![]()
5. Pressure distribution
Using equation (2) the pressure for the external flow is
|
|
|
and for the internal flow
|
|
|
Solving Eq. (22) we get the external pressure
|
|
|
by Eq. (23) the internal pressure
|
|
|
5.1. Bounds for permeability parameter ![]()
We assume that there is a pressure difference at the surface of the sphere, due to which fluid enters and leaves the surface of sphere. At the boundary, the normal filtration velocity
|
|
|
Bounds of permeability parameter for physically possible flow are determined by Leonov [3], from obvious conditions
|
|
using these conditions, we get
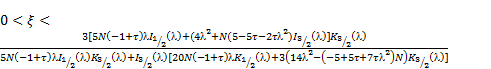 . . | (27) |
Putting ![]() in equation (27), we obtained
in equation (27), we obtained
|
this is calculated by Aparna and Murthy [21].
6. Evaluation of drag force
In order to determine the hydrodynamic drag
force ![]() acting on the sphere,
which is directed along the symmetrical axis, we have used the formula
acting on the sphere,
which is directed along the symmetrical axis, we have used the formula
|
|
where ![]() . Using the equation (13) to (16), the drag on the permeable sphere
due to external flow
. Using the equation (13) to (16), the drag on the permeable sphere
due to external flow
|
|
|
The non-dimensional drag is defined as
|
|
|
7. Result and discussion
At the outset, it is instructive to consider some limiting situations of the drag force as discussed below:
(a) Drag for no-spin on the boundary
It
is interesting to know that by putting ![]() in the calculated drag force (30), we get
in the calculated drag force (30), we get
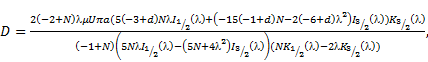 | (32) |
this result is same as earlier reported by Aparna and Murthy [21].
(b) Case of viscous fluid
By putting ![]() and
and
![]() on the constants
on the constants ![]() for viscous fluid, the stream functions are obtained for external
and internal flow, as given below
for viscous fluid, the stream functions are obtained for external
and internal flow, as given below
|
|
||||
|
|
|
As ![]() ,
, ![]() the right hand side of equality (27) tends to 2/7 this leads to
the right hand side of equality (27) tends to 2/7 this leads to ![]() , these results are all in complete agreement with Leonov [3].
, these results are all in complete agreement with Leonov [3].
(c) Micropolar polar fluid past a solid sphere
Substituting
![]() in equation (32) and we
get
in equation (32) and we
get
|
|
this is well known result has been reported by Ramkisoon and Majumdar [12].
The non-dimensional
stream function ![]() at the surface is
given by
at the surface is
given by
|
|
The normal
velocity on the surface of the sphere decreases as ![]() increase
for 0 to
increase
for 0 to ![]() and at
and at ![]() the normal velocity is zero. On the axis
the normal velocity is zero. On the axis![]() the
normal velocity is given by
the
normal velocity is given by
| (37) |
This velocity is less than the velocity ![]() of
the fluid at infinity.
of
the fluid at infinity.
|
|
|
|
Fig. 2. Variation in |
Fig. 3. Dependence of drag w.r.t.
|
|
|
|
|
Fig. 4. Variation of |
Fig. 5. Dependence of |
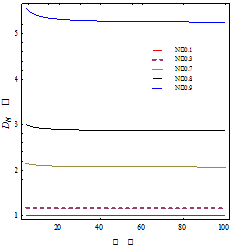
The variation in non-dimensional drag ![]() with respect to micropolar parameter
with respect to micropolar parameter ![]() is
shown in Figure 2. It is clear from the figure that firstly
is
shown in Figure 2. It is clear from the figure that firstly ![]() decreases at
the small values of
decreases at
the small values of ![]() and then drag force reaches almost constant for fix value of
and then drag force reaches almost constant for fix value of ![]() and
and![]() and
and ![]() approaches unity as
approaches unity as ![]() decrease to zero.
decrease to zero.
Variation in the non-dimensional drag ![]() against spin parameter
against spin parameter ![]() (Fig. 3) shows that the
(Fig. 3) shows that the ![]() decreases with the increase in
decreases with the increase in ![]() for
for![]() ,
, ![]() and various value of
coupling number
and various value of
coupling number![]() . The microrotation vector is zero when spin parameter
. The microrotation vector is zero when spin parameter ![]() , in
this case the drag is maximum as shown in Figure 3. This physically shows that
the drag is greater in the case of zero microrotation vector than in the case
of non-zero microrotation vector.
, in
this case the drag is maximum as shown in Figure 3. This physically shows that
the drag is greater in the case of zero microrotation vector than in the case
of non-zero microrotation vector.
|
|
|
|
Fig. 6. The
variation of |
Fig. 7. The
variation of |
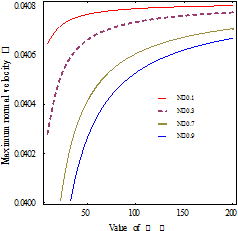
Figure 4 represent the variation of
non-dimensional velocity ![]() on the sphere
on the axis (
on the sphere
on the axis (![]() ) with respect to micropolar parameter
) with respect to micropolar parameter![]() . It is evident as
. It is evident as ![]() increases the normal filtration velocity increases
rapidly.
increases the normal filtration velocity increases
rapidly.
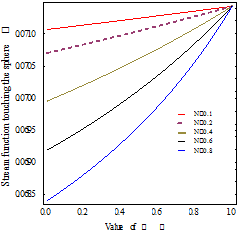
The variation between the stream function
touching the sphere with regard to value of spin parameter ![]() is
shown in Figure 5. Represented that stream function increases with increasing
value
is
shown in Figure 5. Represented that stream function increases with increasing
value ![]() for the fixed value of
for the fixed value of
![]() and
and ![]() .
.
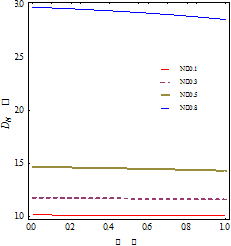
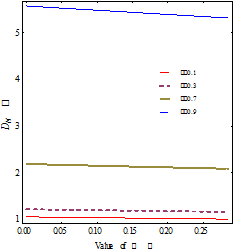
The effect of permeability parameter ![]() on
the non-dimensional drag
on
the non-dimensional drag ![]() is shown in Figure 6. It is evident that
for different value of spin parameter
is shown in Figure 6. It is evident that
for different value of spin parameter ![]() ,
drag decreases continiously as increases the value of
,
drag decreases continiously as increases the value of ![]() where
where
![]() are
the fixed value. When permeability parameter
are
the fixed value. When permeability parameter ![]() the
permeable sphere become impermeable. Figure 6 shows that drag is maximum for
impermeable sphere.
the
permeable sphere become impermeable. Figure 6 shows that drag is maximum for
impermeable sphere.
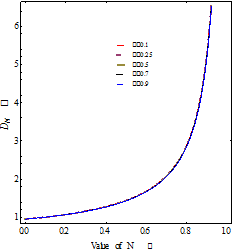
The variation of ![]() with respect to the coupling number
with respect to the coupling number ![]() for
different values of the spin paeameter
for
different values of the spin paeameter![]() shown in Figure 7. It is clear that for
shown in Figure 7. It is clear that for ![]() correspond
to a weak drag and increases rapidly for
correspond
to a weak drag and increases rapidly for ![]() for fix value of
for fix value of ![]() and
and
![]() From Figure 7, it is observed that drag is greater in case of
micropolar fluid than that of newtonian fluid.
From Figure 7, it is observed that drag is greater in case of
micropolar fluid than that of newtonian fluid.
8. Conclusion
The stream function solution to the flow field equation for steady axisymetric creeping flow of micropolar fluid around a permeable sphere are obtained. Different useful results are obtained from the solution, particularly the closed expression for the drag force and the dependence of the drag coefficient on various fluid parameters. It is found that an increase in the spin parameter decreases the drag force experienced by permeable sphere. As the value of permeability parameter increases, the drag force experienced by the sphere decreases continously and, with the increasing of the coupling number, the drag force also increases. The volumetric rate increases with the increasing spin parameter. Maximum normal velocity on the micropolar parameter is also studied. It is observed that the drag is greater in the case of zero microrotation vector than in the case of non-zero microrotation vector.
References
[1] Darcy H., Les Fontaines Publiques, De La Ville De Dijon, Paris, Victor Dalmont, 1856.
[2] Wolfersdorf L.V., Stokes flow past a sphere with permeable surface, Journal of Applied Mathematics and Mechanics 1989, 69, 111-112.
[3] Leonov A.I., The slow stationary flow of a viscous fluid about a porous sphere, Journal of Applied Mathematics and Mechanics 1962, 26, 564-566.
[4] Zeng Yu, Wu Wang-Yi, A new exact solution of the Stokes equation, Chinese Sci. Bull. 1990, 35(14), 1172-1176.
[5] Joseph D.D., Tao L.N., The effect of permeability on the slow motion of a porous sphere in a viscous liquid, Journal of Applied Mathematics and Mechanics 1964, 44, 361-364.
[6] Birikh, R., Rudakoh R., Slow motion of a permeable sphere in viscous fluid, Fluid Dynamics 1982, 17(5), 792-793.
[7] Happel J., Brenner H., Low Reynolds Number Hydrodynamics, Martinus Nijhoff, Publishers, Hague 1983.
[8] Padmavathi B.S., Amarnath T., Palaniappan D., Stokes flow past a permeable sphere-nonaxi-symetric case, Journal of Applied Mathematics and Mechanics 1994, 74, 290-292.
[9] Usha R., Creeping flow with concentric permeable spheres in relative motion, Journal of Applied Mathematics and Mechanics 1995, 75, 644-646.
[10] Vasudeviah M., Malathi V., Slow viscous flow past a spinning sphere with permeable surface, Mechanics Research Communications 1995, 22(2), 191-200.
[11] Eringen A.C., Theory of micropolar fluids, J. Math. Mech. 1966, 16, 1-18.
[12] Ramkisoon H., Majumdar S.R., Drag on an axially symmetric body in the Stokes flow of micropolar fluid, Physics of Fluids 1976, 19, 16-21.
[13] Rao S.K.L., Rao P.B., Slow stationary flow of a micropolar fluid past a sphere, J. Engg. Maths. 1971, 4, 209-217.
[14] Srinivasacharya D., Rajyalakshmi I., Creeping flow of micropolar fluid past a porous sphere, App. Mathematics and Computation 2004, 153, 843-854.
[15] Ramkissoon H., Flow of micropolar fluid past a Newtonian fluid sphere, Journal of Applied Mathematics and Mechanics 1985, 12, 635-637.
[16] Haffmann K.H., Marx D., Botkin N., Drag on spheres in micropolar fluids with non-zero boundary conditions for microrotations, J. Fluid. Mech. 2007, 590, 319-330.
[17] Gupta B.R., Deo S., Stokes flow of micropolar fluid past a porous sphere with non-zero boundary condition for microrotations, International Journal of Fluid Mechanics Research 2010, 37(5), 424-434.
[18] Jaiswal B.R., Gupta B.R., Drag on Reiner-Rivlin liquid sphere placed in micropolar fluid with non-zero boundary condition for microrotations, Int. J. of Appl. Math. and Mech. 2014, 10(7), 90-103.
[19] Gupta B.R., Dev S., Axisymmetric creeping flow of micropolar fluid over a sphere coated with a thin fluid film, Journal of Applied Fluid Mechanics 2013, 6(2), 149-155.
[20] Aparna P., Murthy J.V.R., Nagaraju G., Slow steady rotation of a permeable sphere in an incompressible couple stress fluid, International Journal of Mathematical Archive 2015, 6(2), 1-9.
[21] Aparna P., Murthy J.V.R., Uniform flow of an incompressible micropolar fluid past a permeable sphere, International Electronic Engineering Mathematical Society 2010, 8, 1-10.