Percolation thresholds of 3D all-sided percolation clusters in non-cubic domains
Andrzej Katunin
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
PERCOLATION THRESHOLDS OF 3D ALL-SIDED PERCOLATION CLUSTERS IN NON-CUBIC DOMAINS
Andrzej Katunin
Institute of Fundamentals of Machinery
Design, Silesian University of Technology
Gliwice, Poland
andrzej.katunin@polsl.pl
Received: 30 April
2016; accepted: 21 October 2016
Abstract. The critical 3D all-sided percolation clusters in aL×L×L and aL×aL×L three-dimensional domains with a side length L and an aspect ratio a obtained from continuous percolation problem were analysed in this paper. The simulations of continuous percolation were performed in parallelepiped domains starting from a = 1 and ending at a = 10 using the Monte Carlo algorithm. The resulting percolation thresholds for the simulated domains and percolation clusters as well as variability of number of cells in a domain and in a percolation cluster with variation of a were analysed. The obtained results are useful for evaluation of a content of electrically conducting particles in the dielectric matrix of a composite developed for aircraft lightning strike protection purposes.
Keywords: 3D percolation, percolation threshold, all-sided percolation cluster, percolation in parallelepiped domain, Monte Carlo simulation
1. Introduction
The theory of percolation gains its popularity due to a possibility of probabilistic description of numerous physical phenomena which are characterized by a sudden change of their properties. These phenomena can be described my numerous percolation models developed to date which can be classified, in general, into lattice-based and continuous percolation models (an overview and characterization of these types can be found e.g. in [1]).
In most cases, the simulations of percolation are performed in square or cubic domains for 2D and 3D cases, respectively. It is already known that the percolation is a geometric transition, and thus, it is scale-invariant, however, when considering a non-equal side length of a domain, this invariance may be impaired. Therefore, the influence of an aspect ratio of sides of a domain on properties of percolation systems and, in particular, on critical percolation clusters is one of key issues which has both theoretical and practical reasons, and which has been examined insufficiently to date. The studies on percolation in 2D rectangular domains were initiated by the authors of [2-5]. Later, these studies were continued by Ziff [6], Tsubakihara [7], Watanabe et al. [8, 9] and others. In the same period the extensive studies were performed on 3D non-cubic domains [10-13]. However, one should note that in all of these cases the lattice-based percolation problems were considered. This class of percolation problems is inconsistent to numerous physical phenomena, in particular, to models of polymers and polymeric mixtures which have an amorphous molecular structure, and thus the conducting particles are dispersed randomly in the dielectric matrix, and the continuous percolation model should be applied. The application of such an approach for characterization of critical phenomena occurring in polymers can be found in [14]. The authors of [14] based their study on an all-sided percolation cluster, i.e. the cluster which ensures connectedness between all sides of a domain.
To the best of the author’s knowledge, the investigated problem has not been considered previously, and in the recent study it resulted from practical aspects of manufacturing of composite structures with a conducting filler (see [1, 15, 16]), where the content of a conducting filler needs to be determined in order to obtain a fully conducting composite (i.e. the percolation cluster of a conducting phase needs to be formed). However, based on previously discussed studies, the percolation threshold which characterizes such a cluster may vary depending on the aspect ratio of the side lengths of a domain. This issue has an additional practical aspect, namely, the aircraft structures are usually manufactured in the form of sheets, therefore it is of great interest to evaluate the changes in the percolation threshold with an increase of the aspect ratio.
The performed numerical studies were based on Monte Carlo simulations for three-dimensional parallelepiped domains with side lengths of aL×L×L and aL×aL×L, where L is a side length and a is an aspect ratio for a = 1,…,10. The simulations allow for the finding of the percolation clusters for particular values of a and characterize them with respect to thresholds values.
2. Monte Carlo algorithm and simulations
The developed software is based on a generator of pseudo-random numbers with uniform distribution which generates 3D coordinates of spheres that imitate conducting particles into a 3D dielectric matrix. The algorithm is realized as follows. First, after generation of a certain number of conducting particles, the algorithm checks whether at least one of them is located on the left side of the field of percolation. In the case when such a particle was not found, the number of conducting particles located in the domain is increased by a predefined number of particles k. While in the case when such particle is detected, this particle is considered as a particle that may belong to the percolation cluster, and the searching procedure is performed. For such a particle the radius Rc equaled the double hopping distance (the distance of tunneling of electrical charge between conducting particles - see [1, 17] for details) was defined, and the next particles are searched for in the volume inscribed by Rc. If the searching procedure is successful, found particles are classified as particles belonged to the percolation cluster and the searching procedure is continued in the analogous way. If in this process the formed cluster reaches the rest five sides of a domain, the procedure stops and the percolation thresholds of resulting clusters are calculated. Otherwise, the additional k particles are added to the domain and the searching procedure starts from the beginning [18]. For clarity, the algorithm is presented in the form of block diagram in Figure 1. The described algorithm is similar to the algorithm presented in [1], however it has a direct control of the aspect ratio of side lengths of a domain.
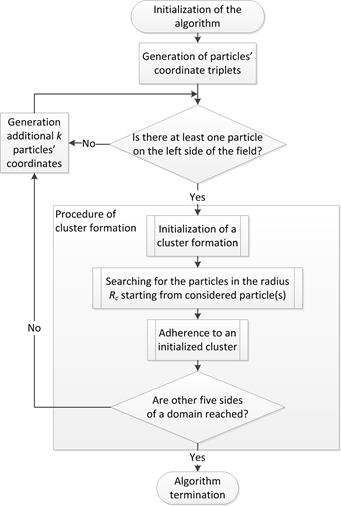
Fig. 1. A block diagram of the percolation cluster formation algorithm
The simulations were performed in the three-dimensional domain with a side length L equivalent to 30 cells and an aspect ratio of a = 1,…,10, thus in the limit cases for the aL×L×L configuration, one obtained a cubic domain of 27000 cells and an elongated domain with a selected side ten times longer than the other 270000 cells, while for the aL×aL×L configuration, the upper limit cases consisted of 2700000 cells. The parameter k for the aL×L×L configuration was set to 3 during simulations, i.e. if the all-sided percolation cluster of n particles was not created in a given run, the next run was performed for n + 3 particles. Such a small value of k increases the accuracy of the obtained solutions. For the aL×aL×L configuration the parameter k was set as functionally dependent on a following the relation 3a2 which allows for significant acceleration of calculation, however, at the cost of accuracy of determination of analysed parameters. In order to verify trends for the aL×aL×L configuration an additional study was performed for L–a×L×L for a = 1,…29 with k = 3. Simulations for each unique set of parameters were repeated 20 times in order to ensure statistical justification of results.
Since the polyaniline was assumed as a conducting filler in the developed composite material [15], the numerical model was parametrized for this material. Following the literature data [19, 20], Rc was assumed to be equal to 1.045·10-4 mm (see the description of numerical experiments in [21] for more details), and the side length of the domain L was assumed to be equal to 0.01 mm.
3. Analysis of obtained results
The obtained results of simulations for both considered configurations of domains for various values of a are presented in Figures 2a 2b, respectively, which contain the averaged values of the numbers of cells that participate in the percolation process with a corresponding percolation threshold, and the number of particles in a percolation cluster with a corresponding clustering threshold with their standard deviations.
|

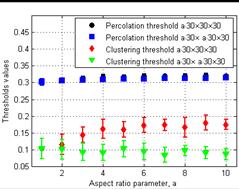
Fig. 2. Influence of the aspect ratio on the numbers of cells and the threshold values for the aL×L×L and aL×aL×L configurations
Analysing the obtained results, one can observe the increase of numbers of cells involved in the percolation process, and the increase of numbers of cells belonging to the percolation cluster with an increase of a which seems to be obvious from the point of view of the geometrical analysis of the system. However, the percolation and clustering thresholds also reveal the increasing trend for the configuration aL×L×L. The increase of these thresholds can be explained by the elongation of the percolation cluster in one direction that leads to an interesting and important property. Namely, if a → ∞ then the percolation, and consequently, the clustering thresholds will increase monotonically to the values of these thresholds which characterize the 1D percolation problem.
The same trends are observed for the configuration aL×aL×L, except the cluster- ing threshold which behaves non-monotonically with an increase of a. This phenomenon can be explained by a still small aspect ratio to consider the problem as the convergent one to the 2D percolation problem. Theoretically, when aL >> L, and thus a → ∞, the formulated problem tends to the 2D percolation problem, and consequently, the percolation and clustering thresholds should increase with an increase of a. In order to verify this tendency, the additional study was performed for the configuration of a domain L–a×L×L for a = 1,…29. The results of these studies are presented in Figures 3a and 3b.
|


Fig. 3. Influence of the aspect ratio on the numbers of cells and the threshold values for the L–a×L×L configuration
These results clearly show that for the increasing aspect ratio, the thresholds increase significantly and reach much higher values than for a cubic-shaped domain. This confirms the convergence of the 3D percolation problem to the 2D one when a increases. According to the observed relations it is possible to approximate the obtained results and use this approximation for description of a percolation system for arbitrary a.
4. Conclusions
The 3D electrical percolation problems in non-cubic domains can be studied using the Monte Carlo simulation. The relation between the aspect ratio of sides lengths of a domain and the resulting percolation and clustering thresholds have been analysed in the performed studies. The obtained results reveal small changes in percolation threshold with a change of the aspect ratio parameter which confirms that this parameter is almost scale-independent. Moreover, it was shown that with an increase of the aspect ratio parameter used in one or two sides, the percolation problems tend to their one or two-dimensional analogues, respectively. By approxi- mation of these trends it is possible to find the percolation threshold for the arbitrary value of the aspect ratio parameter. This relation was helpful for theoretical estimation of the percolation threshold of conducting particles used as a filler in the dielectric matrix of the developed material. The presented procedure is used to determine a content of conducting particles necessary for manufacturing of the composite of conducting and dielectric particles. Further experimental studies [22] on determination of the content of conducting particles necessary to make a resulting material electrically conductive confirmed that the considered content of 30% vol. (following the simulation results obtained in this study) ensures both acceptable electrical conductivity as well as processing parameters during moulding process of the material. Considering the relatively high error occurred in the Monte Carlo simulations of percolation processes (usually more than 10%) the obtained results is in very good agreement with results obtained experimentally.
Acknowledgements
The publication is financed from the funds granted by the Foundation for Polish Science according the contract no. 128/UD/SKILLS/2015 on realization of award granted in the INTER contest, realized within the framework of the SKILLS programme, cofinanced from the European Social Fund. The author would like to thank Prof. Alexander Herega who programmed the software for simulations within the realization of the task in the mentioned research grant.
References
[1] Katunin A., Krukiewicz K., Electrical percolation in composites of conducting polymers and dielectrics, J. Polym. Eng. 2015, 35(8), 731-741.
[2] Monetti R.A., Albano E.V., Critical behavior of the site percolation model on the square lattice in a L × M geometry, Z. Phys. B Con. Mat. 1991, 82(1), 129-134.
[3] Langlands R.P., Pichet C., Pouliot P., Saint-Aubin Y., On the universality of crossing probabilities in two-dimensional percolation, J. Stat. Phys. 1992, 64(3/4), 553-574.
[4] Monetti R.A., Albano E.V., Percolation on the square lattice in a L × M geometry, Z. Phys. B Con. Mat. 1993, 90(3), 351-355.
[5] Monetti R.A., Albano E.V., Density profiles and correlation function of percolating clusters in finite strips, J. Phys. A Math. Gen. 1993, 26(16), 3955-3962.
[6] Ziff R.M., Effective boundary extrapolation length to account for finite-size effects in the percolation crossing function, Phys. Rev. E 1996, 54(3), 2547-2554.
[7] Tsubakihara S., Aspect-ratio dependence of percolation probability in a rectangular system, Phys. Rev. E 2000, 62(6), 8811-8813.
[8] Watanabe H., Yukawa S., Ito N., Hu C.-K., Superscaling of percolation on rectangular domains, Phys. Rev. Lett. 2004, 93(19), 190601.
[9] Watanabe H., Hu C.-K., Mapping functions and critical behavior of percolation on rectangular domains, Phys. Rev. E 2008, 78(4), 041131.
[10] Lorenz C.D., Ziff R.M., Universality of the excess number of clusters and the crossing probability function in three-dimensional percolation, J. Phys. A Math. Gen. 1998, 31(40) 8147-8157.
[11] Lin C.-Y., Hu C.-K., Chen J.-A., Universality of critical existence probability for percolation on three-dimensional lattices, J. Phys. A Math. Gen. 1998, 31(5), L111-L117.
[12] Marrink S.J., Kanckstedt M.A., Percolation thresholds on elongated lattices, J. Phys. A Math. Gen. 1999, 32(44), L461-L466.
[13] Gimel J.C., Nicolai T., Durand D., Crossing probabilities in one, two or three directions for percolation on a cubic lattice, J. Phys. A Math. Gen. 1999, 32(48), L515-L519.
[14] Norizoe Y., Jinnai H., Takahara A., Two-dimensional percolation phenomena of single-component linear homopolymer brushes, J. Chem. Phys. 2014, 140, 054904.
[15] Katunin A., Krukiewicz K., Herega A., Catalanotti G., Concept of a conducting composite material for lightning strike protection, Adv. Mater. Sci. 2016, in press.
[16] Krukiewicz K., Katunin A., The effect of reaction medium on the conductivity and morphology of polyaniline doped with camphorsulphonic acid, Synth. Met. 2016, 214, 45-49.
[17] Catalanotti G., Katunin A., Modelling the electro-mechanical properties of PPy/epoxy conductive composites, Comput. Mater. Sci. 2016, 113, 88-97.
[18] Herega A., Report on the realization of three-dimensional percolation model, Internal report of the project INTER realized according the contract no. 128/UD/SKILLS/2015, Odessa, 20.12.2015.
[19] Bhadra J., Sarkar D., Size variation of polyaniline nanoparticles dispersed in polyvinyl alcohol metrix, Bull. Mater. Sci. 2010, 33(5), 519-523.
[20] Kondawar S.B., Deshpande M.D., Agrawal S.P., Transport properties of conductive polyaniline nanocomposites based on carbon nanotubes, Int. J. Compos. Mater. 2012, 2(3), 32-36.
[21] Katunin A., Analysis of critical percolation clusters of mixtures of conducting and dielectric polymers, J. Appl. Math. Comput. Mech. 2016, 15(1), 59-69.
[22] Katunin A., Krukiewicz K., Turczyn R., Sul P., Łasica A., Bilewicz M., Synthesis and characterization of the electrically conductive polymeric composite for lightning strike protection of aircraft structures, Compos. Struct. 2017, 159, 773-783.

