(D,O)-species of bounded representation type
Nadiya Gubareni
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
(D,O)-SPECIES OF BOUNDED REPRESENTATION TYPE
Nadiya Gubareni
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
nadiya.gubareni@yahoo.com
Received: 11 April
2016; accepted: 29 May 2016
Abstract. We describe weak (D,O)-species of bounded representation type in terms of Dynkin diagrams and diagrams with weights. We reduce the problem of their description to flat mixed matrix problems over discrete valuation rings and their common skew field of fractions.
Keywords: species, (D,O)-species, flat mixed matrix problems, discrete valuation ring, Dynkin diagrams
1. Introduction
The representations of species which are first introduced by P. Gabriel [1] are closely connected with representations of finitely dimensional algebras and Artinian rings and were studied by many authors (see e.g. [1-3]). This paper is devoted to the study of (D,O)-species which can be considered as a type of a generalization of these species. They play an important role in the representation theory of some classes of rings, for example, of right hereditary SPSD-rings. We use the main definitions and results from the previous paper [4].
Let W = (Fi, iMj)i,j Î I be a weak (D,O)-species, where all Fi are equal to Oi or D, and iMj is a (D, D)-bimodule that is finite dimensional both as a right and left D-vector space (see [1]). Let I = {1,2, …, n}. The diagram of W is a directed graph Q(W) whose vertices are indexed by the numbers 1, 2, ..., n, and the number of arrows from a vertex i to a vertex j is
![]() A vertex i of
the graph Q(W) is said to be marked if Fi = Oi and we say that Fi is a
weight of this vertex. A marked vertex is denoted by .
By definition of a weak (D,O)-species, each marked vertex is
minimal in Q(W). The graph obtained from the graph Q(W) with marked
vertices by deleting the orientation of all arrows that connect the unmarked vertices of Q(W) will be called the diagram with weights of a (D,O)-species W. Recall that a
(D,O)-species is of bounded representation type if the dimensions
of its indecomposable finite dimensional representations have
an upper bound.
A vertex i of
the graph Q(W) is said to be marked if Fi = Oi and we say that Fi is a
weight of this vertex. A marked vertex is denoted by .
By definition of a weak (D,O)-species, each marked vertex is
minimal in Q(W). The graph obtained from the graph Q(W) with marked
vertices by deleting the orientation of all arrows that connect the unmarked vertices of Q(W) will be called the diagram with weights of a (D,O)-species W. Recall that a
(D,O)-species is of bounded representation type if the dimensions
of its indecomposable finite dimensional representations have
an upper bound.
In this paper we prove the following theorem, which describes the structure of (D,O)-species of bounded representation type in terms of Dynkin diagrams and diagrams with weights. The proof of this theorem is reduced to solving some flat mixed matrix problems over discrete valuation rings and their common skew field of fractions as it was developed in [4].
Theorem 1. Let {Oi}iÎI be a family of discrete valuation rings with a common skew field of fractions D. A weak (D,O)-species is of bounded representation type if and only if its diagram Q(W) is a finite disjoint union of Dynkin diagrams of the form An, Dn, E6, E7, E8 and the following diagrams with weights:
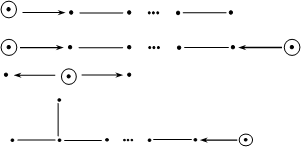
Throughout this paper all rings are assumed to be associative with identity.
2. Proof of the necessity in Theorem 1
Lemma 2.1. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4}. Then a (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
 | (2.2) |
is of unbounded representation type.
Proof. We prove this lemma for the case F1 = O, F2 = F3 = F4 = D, 1M2 = 1M3 = 1M4 = = ODD and iMj = 0 for other i,j Î I. Write J = {1,2,3}.
Let X be a right O-module, Yi
a right D-vector space, and let ![]() be
a D-linear mapping for i Î J.
be
a D-linear mapping for i Î J.
Consider the category Rep(W) whose objects are representations M = (X, Yi, ji,)iÎJ, and a morphism from an object M to an object M¢ = (X¢, Y¢i, j¢i,)i ÎJ is a set of homomorphisms (a, bi) i Î J, in which a: X ® X¢ is a homomorphism of O-modules, bi: Yi ® Y¢i is a homomorphism of D-vector spaces (iÎ J), and the following equalities hold:
| (2.3) |
Let us show that the category Rep(W) is of
unbounded representation type.
Let X be a finitely generated free O-module with basis w1, ... , wn; and let Yi be
a finite dimensional D-space with basis ![]() (i
= 1,2,3). Suppose
(i
= 1,2,3). Suppose
| (iÎ J) (2.4) |
where ![]() for i Î J, s = 1, ..., n.
Then the matrices
for i Î J, s = 1, ..., n.
Then the matrices ![]() , iÎ J, define
the representation M uniquely up to equivalence.
, iÎ J, define
the representation M uniquely up to equivalence.
Let UÎMn(O) be
the matrix corresponding to the isomorphism a, and let ![]() be the matrices corresponding to the isomorphisms bi, i Î J. If
be the matrices corresponding to the isomorphisms bi, i Î J. If ![]() are the matrices corresponding to a representation M¢, then
equalities (2.3) have
the following matrix form:
are the matrices corresponding to a representation M¢, then
equalities (2.3) have
the following matrix form:
| (2.5) |
We obtain the following matrix problem:
Given
a block-rectangular matrix T = ![]() with the following admissible transformations:
with the following admissible transformations:
1. Right O-elementary transformations of columns of T.
2. Left D-elementary transformations of rows within each block Ai (i = 1,2,3).
Set
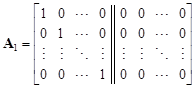 , , |
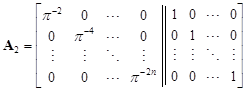 , , 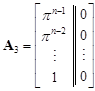 , , |
where p Î R = rad O, p ¹ 0. By [5, Lemma 4], the matrix T is indecomposable and therefore the species with diagram (2.2) is of unbounded representation type.
Lemma 2.6. Let O be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4}. Then a (D,O)-spe-cies W = (Fi, iMj)i,j Î I whose diagram with weights has the form
| (2.7) |
is of unbounded representation type.
Proof. Analogously as in the proof of Lemma 2.1, we obtain the following matrix problem:
Given
a block-triangular matrix T = ![]() . The following transformations are
admitted:
. The following transformations are
admitted:
1. Right O-elementary transformations of columns within the first vertical strip of the matrix T.
2. Right D-elementary transformations of columns within the second vertical strip of the matrix T.
3. Left D-elementary transformations of rows within each horizontal strip of the matrix T.
Reduce A3 to the form ![]() and obtain A2 of the
form
and obtain A2 of the
form ![]() . It is possible to add any row of the
matrix B2 multiplied on the left by elements of D to
any
column of the matrix B1. Thus the matrices A1,
B1 and B2 form the matrix
problem II from [5] and so the (D,O)-species with diagram (2.7)
is of unbounded representation type.
. It is possible to add any row of the
matrix B2 multiplied on the left by elements of D to
any
column of the matrix B1. Thus the matrices A1,
B1 and B2 form the matrix
problem II from [5] and so the (D,O)-species with diagram (2.7)
is of unbounded representation type.
Lemma 2.8. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4,5}. Then a (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
 | (2.9) |
is of unbounded representation type.
Proof. Write J
= {1,2,3,4}. Let X be a right O-module, let Yi be
a right D-vector space for iÎJ, and let ![]() ,
, ![]() (i
= 2,3),
(i
= 2,3), ![]() be D-linear mappings.
be D-linear mappings.
Let Ai be the
matrices corresponding to homomorphisms ji (i Î J) that define the representation M, and ![]() (iÎ J ) be the matrices
corresponding to the represen-
tation M¢. If UÎMn(O)
is the matrix corresponding to the isomorphism a, and
(iÎ J ) be the matrices
corresponding to the represen-
tation M¢. If UÎMn(O)
is the matrix corresponding to the isomorphism a, and ![]() are the matrices corresponding to the isomorphisms bi, iÎ J, then
we have the following matrix equalities:
are the matrices corresponding to the isomorphisms bi, iÎ J, then
we have the following matrix equalities:
| (2.10) |
| (2.11) |
We obtain the following matrix problem:
Given
a block-rectangular matrix T = ![]() which partitioned into
2 horizontal and 3 vertical strips. The
following transformations are admitted:
which partitioned into
2 horizontal and 3 vertical strips. The
following transformations are admitted:
1. Right O-elementary transformations of columns within the first vertical strip of T.
2. Right D-elementary transformations of columns within the second and third vertical strips of T.
3. Left D-elementary transformations of rows within each horizontal strip of T.
Reduce A2 and A4
to the form ![]() and A3 to the form
and A3 to the form
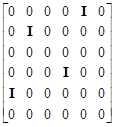 |
In according with this reducing the matrix A1 is divided into 6 horizontal strips and we obtain the following matrix problem.
Given a block-rectangular matrix B partitioned into 6 vertical strips:
|
B1 |
B2 |
B3 |
B4 |
B5 |
B5 |
The following transformations are admitted:
1. Left O-elementary transformations of rows of B.
2. Right D-elementary transformations of columns within each vertical strip Bi (i = 1,2,..,6).
3. If ai £ aj in the poset S:
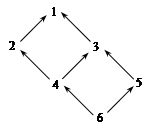
then any column of the vertical strip Bi multiplied on the right by the arbitrary element of D can be added to any column of the vertical strip Bj.
It is easy to see that the blocks B2, B4, B5 form the matrix problem II from [5]. Therefore the species with diagram (2.9) is of unbounded representation type.
Analogously one can prove the following lemma:
Lemma 2.12. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, I = {1,2,3,4,5}. Then a (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
 | (2.13) |
is of unbounded representation type for any directions of arrows.
Lemma 2.14. Let Oi be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical Ri = piOi = Oipi, for i = 1,2; and I = {1,2,3,4}. Then a (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
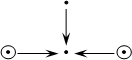 | (2.15) |
is of unbounded representation type.
Proof. Write J
= {1,2,3}. Let Xi be a right Oi-module for i
= 1,2;
Yj a right D-vector space for j = 1,2; and let ![]() , (i = 1,2),
, (i = 1,2), ![]() be D-linear mappings.
be D-linear mappings.
If M = (X1, X2, Y1, Y2, ji,)i ÎJ and M¢ = (X1¢, X2¢, Y1¢, Y2¢, j¢i,)i ÎJ are two equivalent representations of a (D,O)-species W and ai: Xi ® Xi¢ are isomorphisms of O-modules, bi: Yi ® Y¢i are isomorphisms of D-vector spaces (i = 1,2), then the following equalities hold:
| (2.16) |
| (2.17) |
Let Ai be the
matrices corresponding to the homomorphisms ji (i Î J) that
define the representation M,
and ![]() (iÎ J) be the matrices corresponding to
the representation M¢. If Ui
is the matrix with entries in Oi corresponding to
the isomorphism ai, and
(iÎ J) be the matrices corresponding to
the representation M¢. If Ui
is the matrix with entries in Oi corresponding to
the isomorphism ai, and ![]() are the matrices corresponding to the iso-
morphisms bi (i = 1,2), then
equalities (2.16) and (2.17) have the following matrix form:
are the matrices corresponding to the iso-
morphisms bi (i = 1,2), then
equalities (2.16) and (2.17) have the following matrix form:
| (2.18) |
| (2.19) |
We obtain the following matrix problem:
Given a block-rectangular matrix T = ![]() . The following transformations are admitted:
. The following transformations are admitted:
1. Left D-elementary transformations of rows of T.
2. Right O1-elementary transformations of columns of A1.
3. Right O2-elementary transformations of columns of A2.
4. Right D-elementary transformations of columns of A3.
Consider two possible cases.
Case 1: Assume that O1 = O2. Set
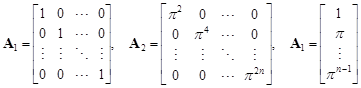 |
By [5, lemma 3], the matrix T is indecomposable. Thus the corresponding representation M of the species W is indecomposable and the species W with diagram (2.15) is of unbounded representation type.
Case 2: Assume
that O1 ¹ O2. Set A1 = A2 = I.
Then T = ![]() and for the matrix A3
we have the matrix problem II from [6]. By [6, Lemma 4.2], this matrix problem
is of unbounded representation type. Therefore, the species with diagram (2.15)
is of unbounded representation type.
and for the matrix A3
we have the matrix problem II from [6]. By [6, Lemma 4.2], this matrix problem
is of unbounded representation type. Therefore, the species with diagram (2.15)
is of unbounded representation type.
Lemma 2.20. Let Oi be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical Ri = piOi = Oipi, for i = 1,2; and I = {1,2,3,4}. Then a (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
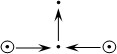 | (2.21) |
is of unbounded representation type.
This lemma is proved as Lemma 2.14.
Note that all diagrams which are not presented in the diagrams of Theorem 1 have a subdiagram of one of the types considered in this section and hence they are of bounded representation type. Therefore, the necessity of Theorem 1 follows from Lemmas 2.1, 2.6, 2.8, 2.12, 2.14, 2.20 and [4, proposition 4.4].
3. Proof of the sufficiency in Theorem 1
Lemma 3.1. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, and let I = {1,2,…,n, n+1}. Then a weak (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
| (3.2) |
is of bounded representation type.
Proof. Write J = {1, 2, ... , n}. Let X
be a right O-module, let Yi be a right D-vector
space for i Î J, and let ![]() ;
; ![]() be D-linear mapping for i = 2, ..., n.
be D-linear mapping for i = 2, ..., n.
If M = (X, Yi, ji)i ÎJ and M¢ = (X¢, Y¢i, j¢i)i ÎJ are two equivalent representations of a (D,O)-species W, a: X ® X¢ is an isomorphism of O-modules and bi: Yi ® Y¢i are isomorphisms of D-vector spaces (i Î J), then the following equalities hold:
| (3.3) |
| (3.4) |
Let Ai be the
matrices corresponding to the homomorphisms ji (i Î J) that
define the representation M,
and ![]() (iÎ J) be the matrices corresponding to
the representation M¢. If UÎMs(O)
is the matrix corresponding to the isomorphism a, and
(iÎ J) be the matrices corresponding to
the representation M¢. If UÎMs(O)
is the matrix corresponding to the isomorphism a, and ![]() are the matrices corresponding to the isomorphisms bi (iÎ J), then equalities (3.3) and (3.4) have the following matrix form:
are the matrices corresponding to the isomorphisms bi (iÎ J), then equalities (3.3) and (3.4) have the following matrix form:
| (3.5) |
Note that the
problem of reducing a set of matrices Ai by matrices Vi
(i = 2, ..., n)
satisfying equalities (3.5) leads to the problem of classifying representations
of
the quiver Q with diagram An-1. By the Gabriel theorem
[1], this
quiver has ![]() indecomposable representations. In
accordance with these representations,
the matrix A1 is partitioned into 2n-2 vertical
strips, and the partial ordering
relation between these strips is linear. Therefore, the matrix problem (3.5)
leads
to the following matrix problem.
indecomposable representations. In
accordance with these representations,
the matrix A1 is partitioned into 2n-2 vertical
strips, and the partial ordering
relation between these strips is linear. Therefore, the matrix problem (3.5)
leads
to the following matrix problem.
Given a rectangular matrix T with entries in a skew field D that is partitioned into 2n-2 vertical strips:
|
T1 |
T2 |
… |
T2n-3 |
T2n-2 |
The transformations of the following types are admitted:
1. Right O-elementary transformations of rows of T.
2. Left D-elementary transformations of columns within each vertical strip Ti.
3. Addition of columns of the i-th vertical strip Ti multiplied on the right by elements of D to columns in the j-th vertical strip Tj if i £ j.
The matrix T can be reduced by these
transformations to the form in which
any block Ti has the form ![]() and
all blocks over and under I are zero. Thus, for any indecomposable
representation M the corresponding matrix T has a finite fixed
number of nonzero elements and this number depends only on n. Therefore,
the species W with diagram (3.2) is of bounded representation type.
and
all blocks over and under I are zero. Thus, for any indecomposable
representation M the corresponding matrix T has a finite fixed
number of nonzero elements and this number depends only on n. Therefore,
the species W with diagram (3.2) is of bounded representation type.
Lemma 3.6. Let Oi be a discrete valuation ring with a common skew field of fractions D and the Jacobson radical Ri = piOi = Oipi for i = 1,2; and let I = {1,2,..., n, n +1}. Then a weak (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
| (3.7) |
is of bounded representation type.
Proof. Renumber the vertices of the diagram (2.16) in such a way that the vertex 1 corresponds to F1 = O1 and the vertex 2 corresponds to F2 = O2. We obtain the diagram
Write J = {1, 2, ..., n–1}.
Let Xi be a right Fi-module (i =
1,2), let Yj be a right
D-vector space for j Î J, and let ![]() ;
; ![]() ;
; ![]() be D-linear mapping for i
= 2, ..., n-1.
be D-linear mapping for i
= 2, ..., n-1.
If M = (X1, X2, Yi, ji, jn)i ÎJ and M¢ = (X1¢, X2¢, Y¢i, j¢i, jn¢)i ÎJ are two equivalent representations of a (D,O)-species W and ai : Xi ® Xi¢ is an isomorphism of O-modules (i = 1,2), bj : Yj ® Y¢j is an isomorphism of D-vector spaces (j Î J), then the following equalities hold:
| (3.8) |
| (3.9) |
Suppose the isomorphism ai is given by the matrix Ui with entries in Oi
for
i = 1,2; and the isomorphism bj is given by the matrix Vj with entries in D
for
j Î J. If Ai, ![]() (i
Î I)
are the matrices corresponding to the representations M, M¢ then
equalities (3.8) and (3.9) are equivalent to the following matrix equalities:
(i
Î I)
are the matrices corresponding to the representations M, M¢ then
equalities (3.8) and (3.9) are equivalent to the following matrix equalities:
| (3.10) |
| (3.11) |
Note that the reduction of a set of matrices Ai, i = 1,3,4, ..., n, by admissible transformations (3.10) and (3.11) leads to the matrix problem of classifying representations of a (D,O)-species W with diagram (3.2) described in Lemma 3.1. After reducing the matrices Ai, i = 1,3,4, ..., n, we get A2 partitioned into n vertical strips and the following matrix problem for A2.
Given a block matrix T with entries in a skew field D that is partitioned into n vertical strips:
|
T1 |
T2 |
… |
Tn |
The transformations of the following types are allowed:
1. Left O2-elementary transformations of rows of T.
2. Right O1-elementary transformations of columns within a vertical strip Tk, for some fixed 1 £ k £ n.
3. Right D-elementary transformations of columns within each vertical strip Ti, if i ¹ k.
4. Addition of columns in the vertical strip Ti multiplied on the right by elements of D to columns in the vertical strip Tj if i £ j.
Using these transformations and taking into
account [5, Lemma 4.1], we can
reduce T to the form in which
every block Ti has the form: U = ![]() or
W =
or
W = ![]() and all
matrices over, under, on the left, and on the right of
the matrix I or, respectively, pmI are zero. This means that the
matrix A2 is
decomposed into a direct sum of matrices of the forms U and W.
and all
matrices over, under, on the left, and on the right of
the matrix I or, respectively, pmI are zero. This means that the
matrix A2 is
decomposed into a direct sum of matrices of the forms U and W.
Thus, the species W with diagram (3.7) is of bounded representation type.
Analogously we can prove the following lemma:
Lemma 3.12. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, and let I = {1,2,…,n, n+1}. Then a weak (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
| (3.13) |
is of bounded representation type.
Lemma 3.14. Let O be a discrete valuation ring with a skew field of fractions D and the Jacobson radical R = pO = Op, and I = {1,2,…,n, n+1}. Then a weak (D,O)-species W = (Fi, iMj)i,j Î I whose diagram with weights has the form
| (3.15) |
is of bounded representation type.
Proof. Write J = {1,2}. Let X be a right O-module, let
Yi be a right D-vector space, and let ![]() be a D-linear mapping for i Î J.
be a D-linear mapping for i Î J.
If M = (X, Yi, ji)i ÎJ and M¢ = (X¢, Y¢i, j¢i)i ÎJ are two equivalent representations of a (D,O)-species W and a: X ® X¢ is an isomorphism of O-modules, bi : Yi ® Y¢i are isomorphisms of D-vector spaces (i Î J), then the following equalities hold:
| (3.16) |
Let U Î Ms(O)
be the matrix corresponding to the isomorphism a, and let ![]() be the matrices corresponding to the isomorphisms bi, iÎ J. If Ai,
be the matrices corresponding to the isomorphisms bi, iÎ J. If Ai,
![]() (i Î J)
are the matrices corresponding to the representations M, M¢ then
equalities (3.14) are equivalent to the following matrix equalities
(i Î J)
are the matrices corresponding to the representations M, M¢ then
equalities (3.14) are equivalent to the following matrix equalities
| (3.17) |
We obtain the following matrix problem.
Given a matrix T = ![]() with entries in D. The transformations
of the follow-
ing types are allowed:
with entries in D. The transformations
of the follow-
ing types are allowed:
1. Right D-elementary transformations of columns within any vertical strip.
2. Left O-elementary transformations of rows of T.
The matrix T can be reduced by these transformations to a direct sum of the following matrices:
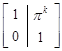 . . |
Thus, a (D,O)-species with diagram (3.15) is of bounded representation type.
The sufficiency in Theorem 1 follows from Lemmas 3.1, 3.6, 3.12, and 3.16.
4. Conclusion
We have described all weak (D, O)-species of bounded representation type. The proof is given by reduction to mixed matrix problems over discrete valuation rings and their common skew field of fractions. We use some facts about representations of quivers and species from [1-3].
References
[1] Gabriel P., Indecomposable representations I, Manuscripta Math. 1972, 6, 71-103.
[2] Dlab V., Ringel C.M., On algebras of finite representation type, Journal of Algebra 1975, 33, 306-394.
[3] Dowbor P., Ringel C.M., Simson D., Hereditary Artinian rings of finite representation type, Representation theory, II. Lecture Notes in Math. 1980, 832, 232-241.
[4] Gubareni N., Representations of (D,O)-species and flat mixed matrix problems, Journal of Applied Mathematics and Computational Mechanics 2016, 3(15), 47-56.
[5] Gubareni N., Structure of finitely generated modules over right hereditary SPSD-rings, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 45-56.
[6] Gubareni N., Some mixed matrix problems over several discrete valuation rings, Journal of Applied Mathematics and Computational Mechanics 2013, 4(12), 47-58.

