Generalized Ostrowski type inequalities for functions whose local fractional derivatives are generalized s-convex in the second sense
Hüseyin Budak
,Mehmet Zeki Sarikaya
,Erhan Set
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
GENERALIZED OSTROWSKI TYPE INEQUALITIES FOR FUNCTIONS WHOSE LOCAL FRACTIONAL DERIVATIVES ARE GENERALIZED S-CONVEX IN THE SECOND SENSE
Hüseyin Budak 1, Mehmet Zeki Sarikaya 2, Erhan Set 3
1,2 Department of Mathematics, Faculty of Science and Arts, Düzce
University, Düzce-Turkey
3 Department of Mathematics, Faculty of Arts
and Sciences, Ordu University, 52200, Ordu, Turkey
hsyn.budak@gmail.com, sarikayamz@gmail.com, erhanset@yahoo.com
Received: 14 March 2016; accepted: 15 September 2016
Abstract. In this paper, we establish some generalized Ostrowski type inequalities for functions whose local fractional derivatives are generalized s-convex in the second sense.
Keywords: generalized Hermite-Hadamard inequality, generalized Hölder inequality, generalized convex functions
1. Introduction
In 1938, Ostrowski established the following interesting integral inequality for differentiable mappings with bounded derivatives [1]:
Theorem
1. (Ostrowski
inequality) Let ![]() be a differentiable mapping on
be a differentiable mapping on ![]() whose derivative
whose derivative ![]() is bounded on
is bounded on ![]() i.e.
i.e.
![]() Then, we have the inequality
Then, we have the inequality
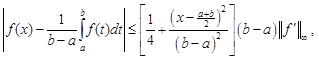 | (1) |
for all ![]() . The constant
. The constant ![]() is the best possible.
is the best possible.
In recent years, the fractal theory has received significant attention. The calculus on the fractal set can lead to better comprehension for the various real world models from science and engineering [2-19].
The purpose of this paper is to establish some
local fractional integral inequalities using generalized s-convex in the
second sense on real linear fractal set ![]()
![]() . This paper is divided into the
following three sections. In Section 2, we give the definitions of the local
fractional derivatives and local fractional integrals and introduce several
useful notations on fractal space which will be used our main results. In
Section 3, the main results are presented.
. This paper is divided into the
following three sections. In Section 2, we give the definitions of the local
fractional derivatives and local fractional integrals and introduce several
useful notations on fractal space which will be used our main results. In
Section 3, the main results are presented.
2. Preliminaries
Recall the set ![]() of
real line numbers and use the Gao-Yang-Kang's idea to describe the definition
of the local fractional derivative and local fractional integral, see [14, 15]
and so on.
of
real line numbers and use the Gao-Yang-Kang's idea to describe the definition
of the local fractional derivative and local fractional integral, see [14, 15]
and so on.
Recently, the theory of Yang’s fractional sets [yang] was introduced as follows.
For ![]() we have the following
we have the following ![]() -type set of element sets:
-type set of element sets:
![]() The
The ![]() -type set of integer is defined as the set
-type set of integer is defined as the set
![]()
![]() The
The ![]() -type set of the rational numbers is
defined as the set
-type set of the rational numbers is
defined as the set ![]()
![]()
![]()
![]() The
The ![]() -type set of the irrational numbers is
defined as the set
-type set of the irrational numbers is
defined as the set ![]()
![]()
![]()
![]() The
The ![]() -type set of the real line numbers is
defined as the set
-type set of the real line numbers is
defined as the set ![]()
If ![]() and
and ![]() belongs the set
belongs the set ![]() of
real line numbers, then
of
real line numbers, then
(1) ![]() and
and ![]() belongs the set
belongs the set ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]() and
and ![]()
The definition of the local fractional derivative and local fractional integral can be given as follows.
Definition
1. [14] A
non-differentiable function ![]()
![]() is called to be local fractional continuous at
is called to be local fractional continuous at ![]() , if for any
, if for any ![]() there
exists
there
exists ![]() such that
such that
holds for ![]() where
where ![]() If
If ![]() is local continuous on the interval
is local continuous on the interval ![]() we denote
we denote ![]()
Definition 2. [14]
The local fractional derivative of ![]() of order
of order ![]() at
at ![]() is
defined by
is
defined by
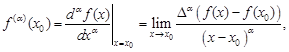 |
where ![]() .
.
If there exists ![]() for any
for any ![]() then
we denoted
then
we denoted ![]() where
where ![]() .
.
Definition 3. [14]
Let ![]() Then the local fractional integral is
defined by,
Then the local fractional integral is
defined by,
with ![]() and
and ![]() where
where
![]()
![]() and
and ![]() is a partition of interval
is a partition of interval ![]()
Here, it follows that ![]() if
if
![]() and
and ![]() if
if ![]() If for any
If for any ![]() there exists
there exists ![]() then
we denote by
then
we denote by ![]()
Lemma 1. [14]
(1) (Local fractional integration is anti-differentiation)
Suppose that ![]() then we have
then we have
(2) (Local fractional integration by parts) Suppose that ![]() and
and ![]()
![]() then we have
then we have
Lemma 2. [14]
Lemma 3. (Generalized
Hölder’s inequality) [14] Let![]()
![]() with
with ![]() then
then
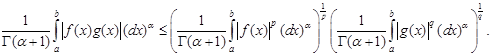 |
In [7], the authors introduced two kinds of
generalized s-convex functions on fractal sets ![]()
![]() as follows:
as follows:
Definition 4. Let ![]() A function
A function ![]() is
said to be generalized s-convex
is
said to be generalized s-convex ![]() in
the first sense, if
in
the first sense, if
for all ![]() and
and ![]() with
with
![]() We denote this by
We denote this by ![]()
Definition 5. A
function ![]() is said to be generalized s-convex
is said to be generalized s-convex
![]() in the second sense, if
in the second sense, if
for all ![]() and
and ![]() with
with
![]() We denote this by
We denote this by ![]()
If we have the reverse
inequality, then![]() is called s-concave.
is called s-concave.
Sarikaya and Budak proved the following generalized Ostrowski inequality in [10]:
Theorem 2. (Generalized Ostrowski
inequality) Let ![]() be an interval,
be an interval, ![]() (
(![]() is
the interior of
is
the interior of ![]() ) such that
) such that ![]() and
and ![]() for
for ![]() with
with ![]() Then,
for all
Then,
for all ![]() we have
the identity
we have
the identity
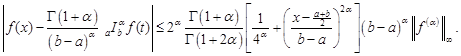 | (2) |
In [8], Mo and Sui established the following
Hermite-Hadamard inequality
for generalized s-convex functions on a real linear fractal set ![]()
![]()
Theorem 3. Suppose
that ![]() is a generalized s-convex
function
in the second sense, where
is a generalized s-convex
function
in the second sense, where ![]() . Let
. Let ![]() ,
, ![]() . If
. If ![]() , then the following inequalities hold:
, then the following inequalities hold:
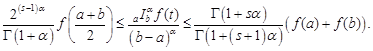 |
If ![]() is a generalized s-concave,
then we have the reverse inequality.
is a generalized s-concave,
then we have the reverse inequality.
3. Main results
We will start with a generalized identity for local fractional integrals:
Theorem 4. Let ![]() be an interval,
be an interval, ![]() (
(![]() is the interior of
is the interior of ![]() ) such that
) such that ![]() and
and ![]() for
for ![]() with
with
![]() . Then, we have the identity
. Then, we have the identity
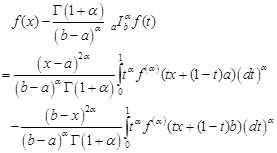 | (3) |
for all ![]()
Proof. Using the local fractional integration by parts (Lemma 1), we have
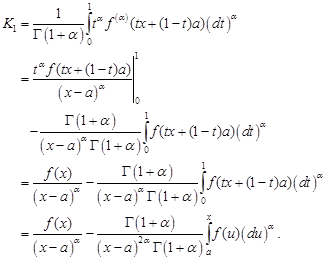 | (4) |
Similarly, we have
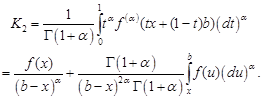 | (5) |
Using (4) and (5), we obtain
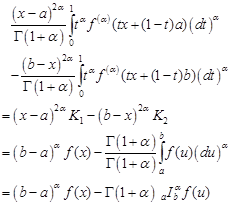 |
which is the required result.
Theorem 5. The
assumptions of Theorem 4 are satisfied. If ![]() is
generalized s-convex in the second sense on
is
generalized s-convex in the second sense on ![]() for
some fixed
for
some fixed ![]() , then we have the inequality
, then we have the inequality
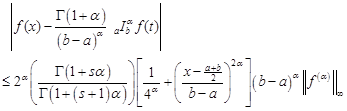 | (6) |
for all ![]() where
where
![]()
Proof. By Theorem 4
and since ![]() is generalized s-convex in the
second sense, then we have
is generalized s-convex in the
second sense, then we have
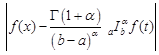
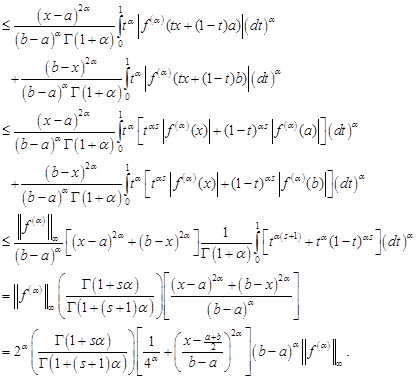 |
Here, we used the fact
and
This completes the proof.
Remark 1. If we
take ![]() in (6), then (6) reduces to (2).
in (6), then (6) reduces to (2).
Corollary 1. Under
assumption of Theorem 5 with ![]() we have
the following midpoint inequality
we have
the following midpoint inequality
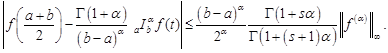 |
Theorem
6. The assumptions
of Theorem 4 are satisfied. If ![]() is generalized s-convex in
the second sense on
is generalized s-convex in
the second sense on ![]() for some fixed
for some fixed ![]() , then we have the inequality
, then we have the inequality
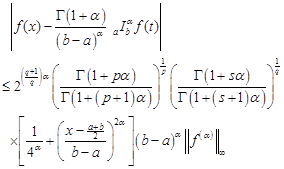 | (7) |
for all ![]() where
where
![]() with
with ![]()
Proof. Taking modulus in (3) and using the generalized Hölder's inequality (Lemma 3), we have
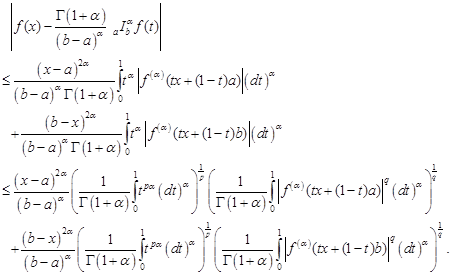 |
Since ![]() is generalized s-convex in the
second sense on
is generalized s-convex in the
second sense on ![]() , then we have
, then we have
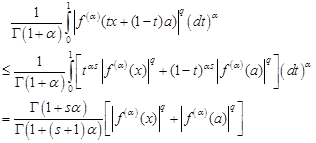 | (8) |
and similarly,
| (9) |
If we substitute the inequality (8) and (9), then we obtain the desired result.
Corollary
2. Under
assumption of Theorem 6 with ![]() we have
the following midpoint inequality
we have
the following midpoint inequality
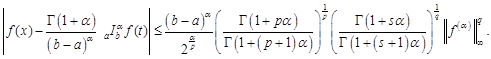 |
Theorem 7. The
assumptions of Theorem 4 are satisfied. If ![]() is
generalized s-concave on
is
generalized s-concave on ![]() for some fixed
for some fixed ![]() , then we have
the inequality
, then we have
the inequality
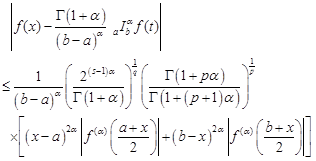 | (10) |
for all ![]() where
where ![]() with
with
![]()
Proof. From Theorem 4 and using generalized Hölder's inequality, we have
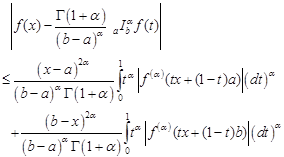
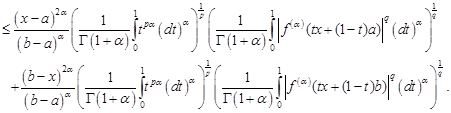 |
Since ![]() is generalized s-concave
on
is generalized s-concave
on ![]() applying Theorem 3, we have
applying Theorem 3, we have
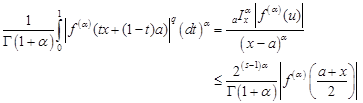 | (11) |
and
| (12) |
If we substitute the inequality (11) and (12), then we obtain the desired result.
Corollary
3. Under
assumption of Theorem 7 with ![]() we have
the following midpoint inequality
we have
the following midpoint inequality
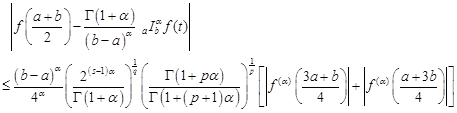 |
where ![]() with
with ![]()
4. Conclusions
In this paper, we presented some Ostrowski type inequalities for function whose local fractional derivatives are generalized s-convex in the second sense. A further study could be assess similar inequalities by using different types of kernels or convexity.
References
[1] Budak H., Sarikaya M.Z., Yildirim H., New inequalities for local fractional integrals, Iranian Journal of Science and Technology (Sciences), in press.
[2] Chen G-S., Generalizations of Hölder's and some related integral inequalities on fractal space, Journal of Function Spaces and Applications Volume 2013, Article ID 198405.
[3] Kılıçman A., Saleh W., Notions of generalized s-convex functions on fractal sets, Journal of Inequalities and Applications 2015, 312. DOI 10.1186/s13660-015-0826-x.
[4] Mo H., Sui X., Yu D., Generalized convex functions on fractal sets and two related inequalities, Abstract and Applied Analysis 2014, Article ID 636751, 7 pages.
[5] Mo H., Generalized Hermite-Hadamard inequalities involving local fractional integrals, arXiv:1410.1062 [math.AP].
[6] Mo H., Sui X., Generalized s-convex function on fractal sets, arXiv:1405.0652v2 [math.AP].
[7] Mo H., Sui X., Hermite-Hadamard type inequalities for generalized s-convex functions on real linear fractal set Rα(0 < α < 1), arXiv:1506.07391v1 [math.CA].
[8] Ostrowski A.M., Über die absolutabweichung einer differentiebaren funktion von ihrem integralmitelwert, Comment. Math. Helv. 1938, 10, 226-227.
[9] Saleh W., Kılıçman A., On generalized s-convex functions on fractal set, JP Journal of Geometry and Topology 2015, 17(1), 63-82.
[10] Sarikaya M.Z., Budak H., Generalized Ostrowski type inequalities for local fractional integrals, RGMIA Research Report Collection 2015, 18, Article 62, 11 p.
[11] Sarikaya M.Z., Erden S., Budak H., Some generalized Ostrowski type inequalities involving local fractional integrals and applications, Advances in Inequalities and Applications 2016, 6.
[12] Sarikaya M.Z., Erden S., Budak H., Some integral inequalities for local fractional integrals, RGMIA Research Report Collection 2015, 18, Article 65, 12 p.
[13] Sarikaya M.Z., Budak H., Erden S., On new inequalities of Simpson's type for generalized convex functions, RGMIA Research Report Collection 2015, 18, Article 66, 13 p.
[14] Yang X.J., Advanced Local Fractional Calculus and Its Applications, World Science Publisher, New York 2012.
[15] Yang J., Baleanu D., Yang X.J., Analysis of fractal wave equations by local fractional Fourier series method, Adv. Math. Phys. 2013, Article ID 632309.
[16] Yang X.J., Local fractional integral equations and their applications, Advances in Computer Science and its Applications (ACSA) 2012, 1(4).
[17] Yang X.J., Generalized local fractional Taylor's formula with local fractional derivative, Journal of Expert Systems 2012, 1(1), 26-30.
[18] Yang X.J., Local fractional Fourier analysis, Advances in Mechanical Engineering and its Applications 2012, 1(1), 12-16.
[19] Yang X.J., Baleanu D., Srivastava H.M., Local Fractional Integral Transforms and their Applications, Elsevier, 2016.

