Cattaneo-Vernotte bioheat transfer equation. Stability conditions of numerical algorithm based on the explicit scheme of the finite difference method
Bohdan Mochnacki
,Wioletta Tuzikiewicz
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
CATTANEO-VERNOTTE BIOHEAT TRANSFER EQUATION. STABILITY CONDITIONS OF NUMERICAL ALGORITHM BASED ON THE EXPLICIT SCHEME OF THE FINITE DIFFERENCE METHOD
Bohdan Mochnacki 1, Wioletta Tuzikiewicz 2
1 University
of Occupational Safety Management in Katowice
Katowice, Poland
2 Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
bmochnacki@wszop.edu.pl, wioletta.tuzikiewicz@im.pcz.pl
Received: 06 October
2016; accepted: 10 November 2016
Abstract. The Cattaneo-Vernotte (CVE) equation is considered. This equation belongs to the group of hyperbolic PDE. Supplementing this equation by two additional terms corresponding to perfusion and metabolic heat sources one can apply the CVE as a mathematical model describing the heat transfer processes proceeding in domain of the soft tissue. Such an approach is recently often preferred substituting the classical Pennes model. At the stage of numerical computations the different numerical methods of the PDE solving can be used. In this paper the problems of stability conditions for the explicit scheme of the finite difference method (FDM) are discussed. The appropriate condition limiting the admissible time step have been found using the von Neumann analysis.
Keywords: bioheat transfer, Cattaneo-Vernotte equation, finite difference method, stability conditions of FDM explicit scheme
1. Introduction
Bioheat transfer processes proceeding in the domain of soft tissue are, as a rule, described using the well known Pennes equation [1-4] being a certain modification of the Fourier parabolic equation. As is well known the mathematical form of this equation, results from the assumption of the infinite velocity of thermal wave propagation. In the case of materials with a specific internal structure (e.g. biological tissue), the Fourier equation should be modified. To take into account the delay effect of the local and temporary heat flux with respect to the temperature gradient, the so-called relaxation time τq is introduced, and then the Cattaneo-Vernotte equation should be considered [5, 6]. According to literature, the relaxation time for the processed meat is the order of seconds (2¸5 s) [6, 7]. As mentioned, the bioheat transfer equation (the tissue model) contains two additional terms determining the perfusion and metabolic heat sources. The first is proportional to the local differences between blood and tissue temperatures. The second term (in this paper) is treated as a constant value. It should be pointed out, that the mathematical form of perfusion heat source results from the assumption that the tissue is supplied by the large number of blood capillaries uniformly distributed in the area under consideration. To take into account the presence of thermally significant vessels of considerable size the so-called vessels models are considered but these problems will not be discussed here.
The primary goal of this paper is to establish the stability conditions for the Cattaneo-Vernotte bioheat transfer equation (in the case when at the stage of numerical modeling, the explicit scheme of the finite difference method is used). The FDM equations are constructed in the version proposed in [8], while at the same time the 2D problem for domains oriented in the Cartesian co-ordinate system is considered.
2. The FDM equations
We consider the following energy equation
| (1) |
where c is the volumetric specific heat of tissue, λ is the thermal conductivity, Q is the capacity of internal heat sources, τq is the relaxation time, T is the temperature, x, y, t denote the geometrical co-ordinates and time.
Additionally
| (2) |
where GB [m3 blood/m3 tissue/s] is the perfusion coefficient, cB is the volumetric specific heat of blood, TB is the arterial blood temperature, Qmet is the metabolic heat source (treated here as a constant value).
So, in the case of bio-heat problems the CVE is of the form
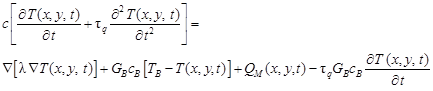 | (3) |
The equation (2) is supplemented by the appropriate boundary and initial conditions. It should be pointed out that the form of typical boundary conditions in the case of CVE is somewhat different than the classic ones. For example, the Neumann condition takes a form
| (4) |
One can see, that for the constant value of the boundary heat flux the condition (4) takes a well known form. The initial conditions determine the initial tissue temperature and initial cooling (heating) rate.
The numerical solution of the problem discussed
can be obtained using the explicit
scheme of the FDM. Let us consider the 2D differential
mesh being the Cartesian product ![]() of the geometrical mesh
of the geometrical mesh ![]() (Fig. 1) and temporal one
(Fig. 1) and temporal one ![]() . Both the geometric h, k and time ∆t mesh steps
are assumed to be the constant values.
. Both the geometric h, k and time ∆t mesh steps
are assumed to be the constant values.

Fig. 1. Rectangular mesh
Below, the FDM equation for the internal nodes will be presented. To simplify the mathematical notation the local numbering of nodes is introduced, in particular the nodes (i, j), (i, j +1), (i, j–1), (i+1, j), (i–1, j) are denoted as 0, 1, 2, 3 and 4.
The FDM approximation of the Cattaneo-Vernotte equation can be taken in the following form
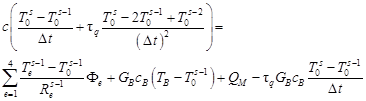 | (5) |
In the case of rectangular differental mesh
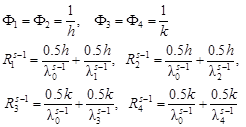 | (6) |
while ![]() are the mesh shape functions and the thermal resistances
between the neighboring
nodes.
are the mesh shape functions and the thermal resistances
between the neighboring
nodes.
The equation (5) can be transformed as follows
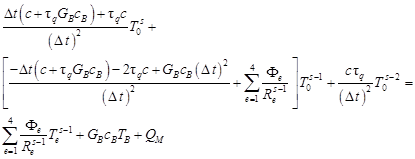 | (7) |
and finally
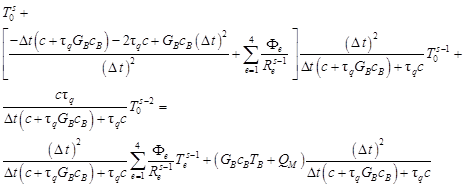 | (8) |
Let us denote
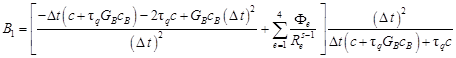 | (9) |
| (10) |
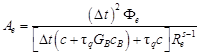 | (11) |
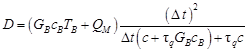 | (12) |
and then
| (13) |
3. Stability condition
The problem of numerical schemes stability is
closely associated with a numerical error. The FDM scheme is stable when the
errors made at one time step of the calculation do not cause the errors to increase
as the computations are continued [9]. If, on the contrary, the errors grow
with time the numerical scheme is said to be unstable. The stability of
numerical schemes can be investigated by performing von Neumann stability
analysis. According to this theory, the approximation error carried by ![]() at every node of space (i, j) = (e)
and time s is assumed to have
a wave form with the wave numbers denoted by w1, w2 and the amplitude by δ:
at every node of space (i, j) = (e)
and time s is assumed to have
a wave form with the wave numbers denoted by w1, w2 and the amplitude by δ:
| (14) |
As time progresses, to assure convergence, the
amplitude of an approximation error must be less than unity, i.e. ![]() [8-10].
[8-10].
Let us introduce the formula (14) into the FDM equation (13)
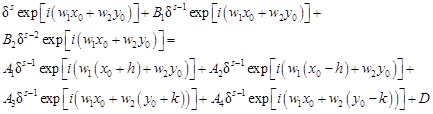 | (15) |
One can see, that for the rectagular mesh and
the constant value of thermal conduc-
tivity ![]()
Additionally the source term can be neglected, because it has no effect on the FDM equation stability. So
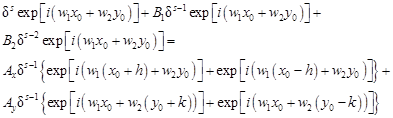 | (16) |
Dividing by δs-2 one obtains
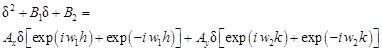 | (17) |
or using the Euler formulas
| (18) |
Denoting
| (19) |
one obtains the equation
| (20) |
According to [9] the absolute values of the roots of equation (20) will be less than 1 when
| (21) |
So, the first inequality takes a form
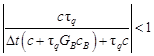 | (22) |
From the last inequality one obtains
| (23) |
or
| (24) |
This inequality is unconditional and does not limit the time step.
Let us consider the second inequality, this means:
| (25) |
The left hand side of (25) can be trasformed in the following way
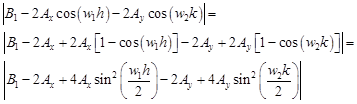 | (26) |
From the view point of FDM equation stability
the most ‘safe’ variant of the last inequality corresponds to ![]() and then
and then
| (27) |
For the constant value of thermal conductivity (see (6)) one obtains
| (28) |
but the transition from (27) to (28) is very tedious.
The final form of CVE stability condition is the following
| (29) |
In the case of non-linear tasks the stability
condition can be also found.
Then each FDM star for transition ![]() must be considered individually
and
the critical time step corresponds to the lowest value, of course.
must be considered individually
and
the critical time step corresponds to the lowest value, of course.
Acknowledgement
This work is supported by the project No. 2015/19/B/ST8/01101 sponsored by National Science Centre (Poland).
References
[1] Pennes H.H., Analysis of tissue and arterial blood temperatures in the resting human forearm, J. Appl. Physiol. 1948, 1, 93-122.
[2] Majchrzak E., Mochnacki B., Jasinski M., Numerical modelling of bioheat transfer in multi-layer skin tissue domain subjected to a flash fire, Computational Fluid and Solid Mechanics 2003, 1-2, 1766-1770.
[3] Jasinski M., Modelling of tissue thermal injury process with application of direct sensitivity method, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 947-957.
[4] Ciesielski M., Mochnacki B., Application of the control volume method using the Voronoi polygons for numerical modeling of bio-heat transfer processes, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 927-935.
[5] Cattaneo M.C., A form of heat conduction equation which eliminates the paradox of instantaneous propagation, C.R. Acad. Sci. I Math. 1958, 247, 431-433.
[6] Roetzel W., Putra N., Das S.K., Experiment and analysis for non - Fourier conduction in materials with non-homogeneous inner structure, Int. J. Therm. Sci. 2003, 42, 541-552.
[7] Antaki P.J., New interpretation of non-Fourier heat conduction in processed meat, ASME J. Heat Transfer 2005, 127, 189-193.
[8] Mochnacki B., Suchy J.S., Numerical Methods in Computations of Foundry Processes, PFTA, Cracow 1995.
[9] Tzou D.Y., Macro - to Microscale Heat Transfer: The Lagging Behavior, John Wiley & Sons, Ltd 2015.
[10] Majchrzak E., Mochnacki B., Dual-phase-lag equation. Stability conditions of a numerical algorithm based on the explicit scheme of the finite difference method, Journal of Applied Mathematics and Computational Mechanics 2016, 15(3), 89-96.
[11] Tuzikiewicz W., Duda M., Bioheat transfer equation. The problem of FDM explicit scheme stability, Journal of Applied Mathematics and Computational Mechanics 2015, 14(4), 139-144.

