Finding the probabilistically-temporal characteristics of Markov G-network with batch removal of positive customers
Mikhail Matalytski
,Victor Naumenko
,Dmitry Kopats
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
FINDING THE PROBABILISTICALLY-TEMPORAL CHARACTERISTICS OF MARKOV G-NETWORK WITH BATCH REMOVAL OF POSITIVE CUSTOMERS
Mikhail Matalytski 1, Victor Naumenko 2, Dmitry Kopats 2
1 Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
2 Faculty of Mathematics and Computer Science, Grodno State University
Grodno, Belarus
m.matalytski@gmail.com, victornn86@gmail.com
Received: 04 May
2016; accepted: 11 July 2016
Abstract. The investigation of a Markov queueing network with positive and negative customers and positive customers batch removal has been carried out in the article. The purpose of the research is analysis of such a network at the non-stationary regime, finding the time-dependent state probabilities and mean number of customers. In the first part of this article, a description of the G-network operation is provided with one-line queueing systems. When a negative customer arrives to the system, the count of positive customers is reduced by a random value, which is set by some probability distribution. Then for the non-stationary state probabilities a Kolmogorov system was derived of difference-differential equations. A technique for finding the state probabilities and the mean number of customers of the investigated network, based on the use of an apparatus of multi- dimensional generating functions has been proposed. The theorem about the expression for the generating function has been given. A model example has been calculated.
Keywords: G-network, positive and negative customers, customers batch removal, non-stationary regime, generation function, state probabilities
1. Introduction
G-networks or queueing networks with positive and negative customers was introduced by Gelenbe [1]. Such networks with batch removal of positive customers are used in the development of computer systems and networks models, in which defective problems (negative customers) destroy tasks or user jobs (positive customers). Task handlers are the processes running on servers; customers - user jobs for processing [2].
Let’s consider an open G-queueing network
with ![]() single-line queueing
systems (QS). To the
single-line queueing
systems (QS). To the ![]() system external environment (QS
system external environment (QS ![]() ) a simple flow
of customers arrives with the rate
) a simple flow
of customers arrives with the rate ![]() and
a simple flow of negative customers with the rate
and
a simple flow of negative customers with the rate ![]() ,
, ![]() . All customer flows that arrive to the network are independent. The
service durations of positive customers in i-th QS distributed
exponentially with the rate
. All customer flows that arrive to the network are independent. The
service durations of positive customers in i-th QS distributed
exponentially with the rate ![]() ,
, ![]() .
.
In the articles [3-5], a G-network at a transient (non-stationary) regime has been investigated. At that negative customer, arrivining to the system, where there were positive customers, immediately destroy one of them, and then immediately left the network, not having received service in the QS. In the article [6] was conducted analysis at non-stationary regime of G-network with signals, and in the article [7] - G-network with signals with random delay.
In this paper, we describe in more detail the
other behaviors of negative
customers, which arrive to the
network systems. Let at time t in the system ![]() there are
there are ![]() positive customers, where
positive customers, where ![]() - integer random value. Negative customer arriving to the some system of the network instantly destroys
(removes from the network) destroyed
immediately
- integer random value. Negative customer arriving to the some system of the network instantly destroys
(removes from the network) destroyed
immediately ![]() of positive customers. If
of positive customers. If ![]() , the system
, the system ![]() completely is
devastated (all positive customers, which are in this QS at a given time are immediately destroyed). Thus,
random value
completely is
devastated (all positive customers, which are in this QS at a given time are immediately destroyed). Thus,
random value ![]() , which effectively deter-
mines the maximum size of the destruction batch of customers in QS
, which effectively deter-
mines the maximum size of the destruction batch of customers in QS ![]() , is subject to an arbitrary discrete distribution law:
, is subject to an arbitrary discrete distribution law:
| (1) |
Gelenbe studied such behavior of negative customers considering signals in the paper [8], but only at stationary regime.
As previously explained, in each network system only
positive customers are serviced. A
positive customer serviced in the QS ![]() , with probability
, with probability ![]() sent to
the QS
sent to
the QS ![]() as a positive customer, with a probability
as a positive customer, with a probability ![]() - as a negative customer, and
with probability
- as a negative customer, and
with probability ![]() leaving
from the network to the external environment (QS
leaving
from the network to the external environment (QS ![]() ),
), ![]() .
.
The state of the network at time ![]() meaning the vector
meaning the vector
| (2) |
which forms a Markov random process with a
countable number of states, where state ![]() means
that at time
means
that at time ![]() in QS
in QS ![]() there are
there are ![]() of positive customers,
of positive customers, ![]() .
.
2. The system of the difference-differential Kolmogorov equations for the network state probabilities
We
introduce some notations. Let’s ![]() - probability of the network state
- probability of the network state ![]() at time
at time ![]() ;
; ![]() - Heaviside function,
- Heaviside function, ![]() ;
; ![]() - a vector of dimension
- a vector of dimension ![]() , consisting of
zeros, except for the component with number of
, consisting of
zeros, except for the component with number of ![]() , which is equal
to 1,
, which is equal
to 1, ![]() . Let’s allows
. Let’s allows
| (3) |
There are following transitions of a random
process ![]() to the state
to the state ![]() during
time
during
time ![]() :
:
1) from the state ![]() , in this case, during time
, in this case, during time ![]() a positive customer arriving to the QS
a positive customer arriving to the QS ![]() with probability
with probability ![]() ;
;
2) from the state ![]() , wherein the positive customer leaves
the network
or in an external environment passes into QS
, wherein the positive customer leaves
the network
or in an external environment passes into QS ![]() as a
negative customer,
if it had no customers; the probability of such an event equals
as a
negative customer,
if it had no customers; the probability of such an event equals ![]() ;
;
3) from the states ![]() , in this case a negative customer
arrives to the QS
, in this case a negative customer
arrives to the QS ![]() and destroys a random batch
of positive customers; the probability of such event is equal to
and destroys a random batch
of positive customers; the probability of such event is equal to ![]() ;
;
4) from the state ![]() , in this case, after the servicing of a
positive customer
in the QS
, in this case, after the servicing of a
positive customer
in the QS ![]() it goes to the QS
it goes to the QS ![]() ; the probability of such an event is
equal to
; the probability of such an event is
equal to ![]() ;
;
5) from the states in
this case, after the servicing of a positive customer in the QS ![]() it goes to the QS
it goes to the QS ![]() as a negative customer, which destroys
in it random batch of positive customers; the probability of such an event is
equal to
as a negative customer, which destroys
in it random batch of positive customers; the probability of such an event is
equal to ![]() ;
;
6) from the state ![]() , while in each QS
, while in each QS ![]() ,
, ![]() ,
there are no positive
customers nor any negative customers arriving, and which during
,
there are no positive
customers nor any negative customers arriving, and which during ![]() was
not to serviced by any customer; the probability of such event is equal to
was
not to serviced by any customer; the probability of such event is equal to ![]() ,
, ![]() ;
;
7) of the remaining states with a probability ![]() .
.
Then, using the formula of total probability, we shall have
| (4) |
Dividing both sides of this relation by ![]() and passing to the limit
and passing to the limit ![]() we obtain that the non-stationary
states probabilities of the considered network satisfy the following system of
difference-differential equations
we obtain that the non-stationary
states probabilities of the considered network satisfy the following system of
difference-differential equations
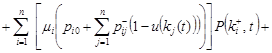
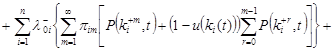 (5) (5)
|
Suppose that all systems of the network
operating in a heavy traffic regime,
i.e. ![]() ,
, ![]() ,
, ![]() .
Taking this assumption into account, the system (5) takes the form
.
Taking this assumption into account, the system (5) takes the form
| (6) |
3. Finding network state probabilities using the generating function
Denote by
![]() , where
, where ![]() ,
, ![]() , n-dimensional generating function:
, n-dimensional generating function:
| (7) |
Multiplied (6) on ![]() and adding together all possible values
and adding together all possible values ![]() from 0 to
from 0 to ![]() ,
, ![]() , obtain:
, obtain:
| (8) |
Consider some sums, contained on the right side of (8). Let’s allows
then we can show that
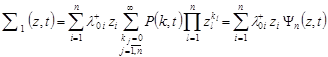 . . |
For the sum of ![]() we
have:
we
have:
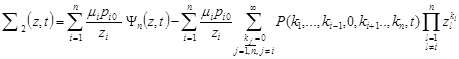 . . |
For the sum of ![]() we
will have:
we
will have:
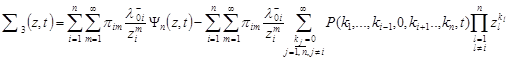 . . |
For the sum of ![]() we
obtain:
we
obtain:
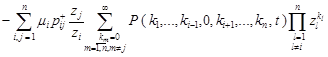 . . |
And finally, for the last sum
we shall have:
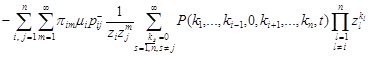 . . |
Therefore, the generating function is a fairly ordinary inhomogeneous linear ordinary differential equation
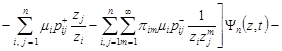
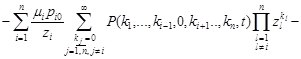
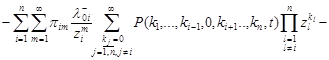
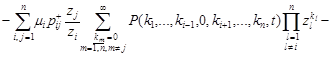
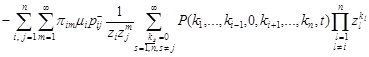 . . | (9) |
Since all of the whole QS network operate under high load conditions, the last two expressions in the form of the sums in equation (9) will be zero, and it becomes homogeneous:
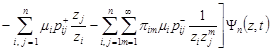 . . |
Its general solution has the form
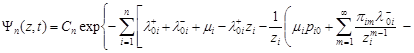
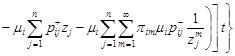 . . | (10) |
We assume that at the initial moment of time,
the network is in state ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Then the initial condition for the
last equation (10) will be
. Then the initial condition for the
last equation (10) will be ![]() . Using it, we
obtain
. Using it, we
obtain ![]() . Thus,
the expression for the generating function
. Thus,
the expression for the generating function ![]() has
the form
has
the form
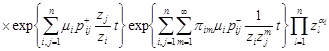 , , | (11) |
where
To find the probability of the network states, we transform (11) to a convenient form by expanding its member exhibitors in a Maclaurin series. We can show that the statement is true.
Theorem. The expression for the generating function can be represented in the form
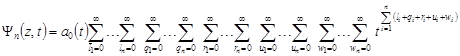
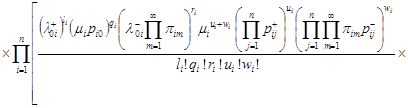
| (12) |
where ![]() ,
, ![]() .
.
The probability ![]() can
be found as the coefficient of
can
be found as the coefficient of ![]() in the expansion of
function
in the expansion of
function ![]() in multiple series (12), and the mean
number of customers in the system
in multiple series (12), and the mean
number of customers in the system ![]() in the form
in the form ![]() .
.
4. Model example
In this example the count of QS ![]() lets
arriving probabilities of customers to i-th QS be
respectively equal
lets
arriving probabilities of customers to i-th QS be
respectively equal ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() ,
, ![]() .
.
Consider the time interval ![]() . As a time unit we take 1 hour, then
. As a time unit we take 1 hour, then ![]() h. Let the arriving rates
of positive and negative customers be respectively equal
h. Let the arriving rates
of positive and negative customers be respectively equal ![]() and
and ![]() .
Let’s arriving rates of positive and negative customers to each QS
.
Let’s arriving rates of positive and negative customers to each QS ![]() and
and ![]() ,
taking into account that
,
taking into account that ![]() ,
, ![]() ,
, ![]() ,
respectively will be equal:
,
respectively will be equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Suppose, that service rates of
customers in QS are equal:
. Suppose, that service rates of
customers in QS are equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Let us also transition probabilities of
positive and negative customers between QS be equal ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Calculations have shown that ![]() .
.
Let’s a
random value ![]() has a Poisson distribution
with parameter
has a Poisson distribution
with parameter ![]() and let
and let ![]() , then (1) takes form
, then (1) takes form ![]() ,
, ![]() ,
, ![]() . Let also
. Let also ![]() .
.
We need to find, for example, state
probability ![]() . It is the coefficient of
. It is the coefficient of ![]() in the expansion of
in the expansion of ![]() in multiple series (12), so that
the degree of
in multiple series (12), so that
the degree of ![]() must satisfy the
relation
must satisfy the
relation ![]() ,
, ![]() ,
where
,
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Hence, it follows that
. Hence, it follows that
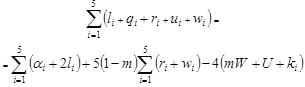 |
Then from (12) we find that
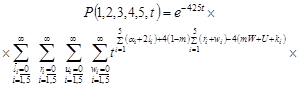
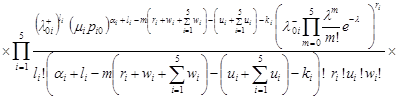
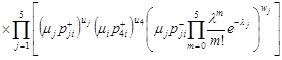 . . |
Figure 1 shows a chart of the state
probability ![]() for different
for different ![]() on the
condition that at the initial time, the network is in a state of
on the
condition that at the initial time, the network is in a state of ![]() ,
, ![]() .
.
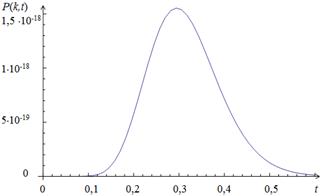
Fig. 1. The chart of
the state probability ![]()
Calculating the partial derivative of the generating function (12) by variable zi in dot z = (1,1,…,1), and carrying out a series of mathematical transformations, we find that the mean number of customers in the queue system Si is calculated by the formula
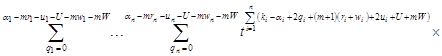
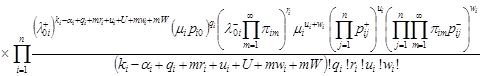 . . |
Figure 2 shows a plot of changes of the mean
number of customers in QS ![]() .
.
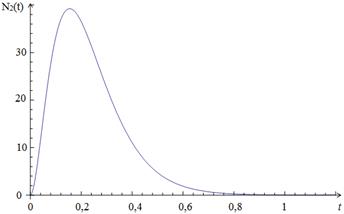
Fig. 2. The chat for changes of the mean number of positive customers N2(t) in QS S2
5. Conclusions
In the article an investigation of Markov G-network was conducted in the case when a negative customer can destroy a random batch of positive customers. For such a network operating under a heavy traffic regime, finding a technique for non-stationary state probabilities and a mean number of customers in network systems was proposed using an apparatus based on the use of multivariate generating functions.
References
[1] Gelenbe E., Product form queueing networks with negative and positive customers, Journal of Applied Probability 1991, 28, 656-663.
[2] Naumenko V., Pankov A., Kopats D., Investigation of Markov G-network with positive customers batch removal in transient regime. [In Russian: Issledovaniye markovskoy G-seti s gruppovym udaleniyem polozhitel'nykh zayavok v perekhodnom rezhime]. Vestnik of GrSU. Ser 2, 2016, 3.
[3] Matalytski M., Naumenko V., Stochastic networks with non-standard customers movement. [In Russian: Stokhasticheskiye seti s nestandartnymi peremeshcheniyami zayavok], Monograph, GrSU, Grodno 2016.
[4] Naumenko V., Matalytski M., Network analysis with positive and negative requests in transitional mode. [In Russian: Analiz seti s polozhitel'nymi i otritsatel'nymi zaiavkami v perekhodnom rezhime], Vestnik of GrSU, Ser 2. 2016, 3(159), 135-142.
[5] Matalytski M., Naumenko V., Non-stationary analysis of queueing network with positive and negative messages, Journal of Applied Mathematics and Computational Mechanics 2013, 12(2), 61-71.
[6] Matalytski M., Naumenko V., Investigation of G-network with signals at transient behavior, Journal of Applied Mathematics and Computational Mechanics 2014, 13(1), 75-86.
[7] Matalytski M., Naumenko V., Investigation of G-network with random delay of signals at non-stationary behavior, Journal of Applied Mathematics and Computational Mechanics 2014, 13(3), 155-166.
[8] Gelenbe E., G-networks with signals and batch removal, Probability in the Engineering and Informational Sciences 1993, 7, 335-342.

