Export balancing method of production-consumption model
Ewa Ładyga
,Marek Ładyga
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
EXPORT BALANCING METHOD OF PRODUCTION-CONSUMPTION MODEL
Ewa Ładyga, Marek Ładyga
Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
ewa.ladyga@im.pcz.pl, marek.ladyga@im.pcz.pl
Received: 15 October
2016; accepted: 15 November 2016
Abstract. This paper presents an export balancing method of the production-consumption model. All contractors have their share in balancing the model, and the compromise they reach is determined explicitly and precisely according to the requirements of decision-makers.
Keywords: export balancing method, unsustainable production-consumption model
1. Introduction
In every society there are producers, who must produce something to make a profit and consumers, who must buy something to meet their needs. When the whole production is absorbed by the market, and producers are not interested in expanding it, then we have the so called natural balance [1]. Because of the fact that the Polish economy is limited due to supplies, conflicts arise between producers and consumers quite often. The issue of conflicting goals of producers (increase in production) and consumers (decrease in demand) is shown in [2]. The method of mutual compromise between contractors to balance demand and supply consists in:
a) determining benchmarks and their scopes, which will allow one to reach a compromise in the unsustainable production-consumption model, where the demand for particular goods exceeds their supply,
b) determining mutual relationships between particular contractors and benchmarks,
c) evaluating the scope of compromise in case of all contractors on the basis of the above-mentioned data.
This paper presents the unsustainable production-consumption model, in which contractors, including producers and consumers of particular goods, play a part.
2. The solution of the problem
In this model it is assumed that the total supply of goods does not cover the total demand for them in a given period of time, which can be shown in the form of the - mentioned demand and supply vector fulfilling the following conditions:
1) ![]() ,
,
2) ![]() ,
,
3) ![]() .
.
The first coordinates (from 1 to m) of the vector ![]() , denoted by positive
numbers represent producers supply. The final coordinates
, denoted by positive
numbers represent producers supply. The final coordinates ![]() of the vector
of the vector ![]() denoted
by negative numbers represent consumers demand. Condition no. 3 shows that the
production does not cover the demand for particular goods. To balance
the model (when supply equals demand) contractors must make concessions.
The possible maximum concessions are denoted by the vector fulfilling
denoted
by negative numbers represent consumers demand. Condition no. 3 shows that the
production does not cover the demand for particular goods. To balance
the model (when supply equals demand) contractors must make concessions.
The possible maximum concessions are denoted by the vector fulfilling ![]() the following conditions:
the following conditions:
1) ![]() ,
,
2) ![]() .
.
For ![]()
![]() means a maximum possible increase in
production of this pro-
ducer. For
means a maximum possible increase in
production of this pro-
ducer. For ![]()
![]() means a maximum possible decline in
demand of this con-
sumer. Condition no. 2 makes balancing possible, as the
total possible number
of concessions of all the contractors is smaller than the number needed to
balance the model.
means a maximum possible decline in
demand of this con-
sumer. Condition no. 2 makes balancing possible, as the
total possible number
of concessions of all the contractors is smaller than the number needed to
balance the model.
The question is which contractor should verify their demand or supply and to what extent.
Let’s assume that KR is not an empty set of benchmarks (the power sets KR is equal) on the basis of which it is decided which contractor should verify their demand or supply and to what extent. The KR set may include both minimum and maximum benchmarks as well as conditions imposed by contractors. To find out to what extent all contractors meet particular benchmarks, the following mapping must be used:
| (1) |
the ![]() , one that
, one that ![]() .
.
The real
number indicates ![]() to what extent the i-contractor meets
j-bench-
marks. It is convenient to present the mapping values f in the
form of a matrix
to what extent the i-contractor meets
j-bench-
marks. It is convenient to present the mapping values f in the
form of a matrix
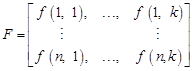 |
J-column of the matrix represents how all contractors behave towards j-benchmark.
By contrast, i-row shows to what extent a given j-contractor
meets particular benchmarks. So as to compare the values for various ![]() contractors
and various benchmarks the matrix F must be normalized. Let the vector
contractors
and various benchmarks the matrix F must be normalized. Let the vector ![]() be a vector of particular benchmark
weights, meaning
for each one
be a vector of particular benchmark
weights, meaning
for each one ![]() and
and ![]() , where
, where ![]() ,
, ![]() is the scalar product of
is the scalar product of ![]() and
and ![]() vectors. Taking into account the
above-mentioned requirements, it is necessary to use the matrix coupled with f
mapping, the matrix
is denoted by,
vectors. Taking into account the
above-mentioned requirements, it is necessary to use the matrix coupled with f
mapping, the matrix
is denoted by, ![]() where
where 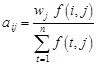 .
.
Aggregation of ![]() i-row
of the matrix allows for evaluation of
i-contractor’s attitude towards all benchmarks. Hence, there is a vector
i-row
of the matrix allows for evaluation of
i-contractor’s attitude towards all benchmarks. Hence, there is a vector
![]() introduced, which is of vital
importance while
determining concessions of contractors. This vector has been called the price
of contractors concessions.
introduced, which is of vital
importance while
determining concessions of contractors. This vector has been called the price
of contractors concessions.
Having assigned three vectors:
a) demand-supply
| (2) |
b) maximum concession
| (3) |
c) the price of contractors’ concessions with regard to benchmarks
| (4) |
and assuming:
| (5) |
for ![]() we define the following values:
we define the following values:
| (6) |
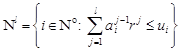 | (7) |
where
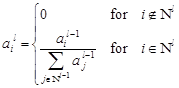 | (8) |
| (9) |
![]() =
= ![]()
where
 | (10) |
The iterative process (2)-(10), the properties
of which are discussed in [3],
is finished for such a s-iteration
that ![]() .
.
In the presented algorithm, it is assumed
that users are acquainted with
the mechanism responsible for economic phenomena and they generally know what
elements the set of benchmarks KR should contain and what values should be
assigned ![]() to mapping. The problem of the explicit
indication of vector
to mapping. The problem of the explicit
indication of vector ![]() is presented in the following statement.
is presented in the following statement.
If:
a) ![]() ,
, ![]() the price of contractors concessions
with
regard to benchmarks,
the price of contractors concessions
with
regard to benchmarks,
b) vectors ![]() i
i ![]() are 1-fold
are 1-fold ![]() iterations of the vector which are
achieved by means of vectors
iterations of the vector which are
achieved by means of vectors ![]() ,
, ![]() and
and ![]() ,
, ![]() then
then
![]() .
.
According to this statement, the vector of demand and supply in each iteration, that is to say the vector which balances the model, is indicated accurately to the price of contractors concessions with regard to benchmarks. Unfortunately, because of insufficient knowledge, the explicit indication of the set KR, f mapping values, (1), and by extension the matrix coupled with f mapping, is not always possible. It happens sometimes that the knowledge on the mechanism of economic phenomena which are to be explored is so limited that all one can do is try to stick to a list of elements which are more or less adequate to the set KR [4, 5]. The same situation may occur in the case of indication of f mapping values. The question appears which elements out of the ones from the set KR should be taken into account, and which ones should be rejected, as taking all of them into account could aggravate the problem and blear their real scopes. In my opinion, in such cases, experts opinions should be considered. If a given team is well-chosen, that is to say there are very reliable experts who specialize in problematic aspects of the analysed phenomenon and its circumstances, then as a result of consultation and compilation of their opinions, it will be possible to decide which elements should be included in the set KR and what values should be assigned to f mapping. However, if the experts represent different types of corporations, their opinions may differ [4]. Then, instead of one matrix coupled with the adjusting mapping one will get a few different variants.
Let’s assume that ![]() means
i-vector, which balances the production and consumption model achieved
by means of iteration (2)-(10) on the basis of i matrix coupled with f
mapping. While
means
i-vector, which balances the production and consumption model achieved
by means of iteration (2)-(10) on the basis of i matrix coupled with f
mapping. While ![]() means a real number (not a negative one) which is matched with
the vector
means a real number (not a negative one) which is matched with
the vector ![]() . This number is called a vector
usability measure
. This number is called a vector
usability measure ![]() for
for ![]() .
.
Since numbering
of vectors is arbitrary, one can assume that ![]() the
sequence is non-decreasing, where t is a number of matrices coupled with
f mapping (1). The alternative solution is a solution
in which users choose one of the vectors from the
specialized U set. The alternative solution can work out only when it is
acceptable in reality [5]. That is why
the following rule of communication of the U set
is applied.
the
sequence is non-decreasing, where t is a number of matrices coupled with
f mapping (1). The alternative solution is a solution
in which users choose one of the vectors from the
specialized U set. The alternative solution can work out only when it is
acceptable in reality [5]. That is why
the following rule of communication of the U set
is applied.
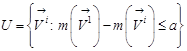 , where a is a real number determined in advance and belonging to the range
, where a is a real number determined in advance and belonging to the range ![]() .
.
The
question how to choose a number ![]() must still be answered. I would suggest
using an export method. Mapping does
must still be answered. I would suggest
using an export method. Mapping does ![]() not
need to be explicitly
determined. Thus, one can get different variants of A matrix coupled with f map-
ping. It is assumed that there are t
of such matrices
not
need to be explicitly
determined. Thus, one can get different variants of A matrix coupled with f map-
ping. It is assumed that there are t
of such matrices ![]() As a result one can get
solutions
As a result one can get
solutions ![]() where
where ![]() , n means
a number of contractors,
, n means
a number of contractors, ![]() . Using a group of
experts, each solution may be assigned to some measure of meaningfulness
. Using a group of
experts, each solution may be assigned to some measure of meaningfulness ![]() . It is assumed that this group amounts
to
. It is assumed that this group amounts
to ![]() people. Each
expert assigns each solution some
non-negative number
people. Each
expert assigns each solution some
non-negative number ![]() for
for ![]() ,
, ![]() . The number
. The number ![]() defines
the measure of meaningfulness of i-solution carried out by j-expert.
It must be noted that number sequences
defines
the measure of meaningfulness of i-solution carried out by j-expert.
It must be noted that number sequences ![]() ,
, ![]() , …,
, …,![]() should be sequences of the same rows.
Otherwise, some number sequences for
should be sequences of the same rows.
Otherwise, some number sequences for ![]() must be normalized
so that they could match sequences rows
must be normalized
so that they could match sequences rows ![]() for
for
![]() ,
, ![]() .
Having assigned values
.
Having assigned values ![]() for
for ![]() ,
, ![]() , one should
calculate the initial measure of
i-solution, as an arithmetic mean of i-solution carried out by
all the experts.
If the initial measure of i-solution is denoted by
, one should
calculate the initial measure of
i-solution, as an arithmetic mean of i-solution carried out by
all the experts.
If the initial measure of i-solution is denoted by ![]() :
:
Normalizing these initial measures to unit one gets:
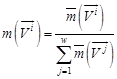 for for |
The solutions ![]() are arranged in non-increasing sequence
according to the measures
are arranged in non-increasing sequence
according to the measures ![]() .
.
Let ![]() .
.
The U set contains only these vectors ![]() , the measure
, the measure ![]() of which differs from the solution having
the biggest measure by no more than a. I suggest
the number a is a percent of difference between
of which differs from the solution having
the biggest measure by no more than a. I suggest
the number a is a percent of difference between ![]() and
and
![]() . The percent is determined by the
algorithm user. If a is smaller than the difference
. The percent is determined by the
algorithm user. If a is smaller than the difference ![]() , the U set contains only
, the U set contains only ![]() solution. If a
is bigger than the difference
solution. If a
is bigger than the difference ![]() , the U set
contains all the solutions:
, the U set
contains all the solutions: ![]() . Thus, the
conclusion is that for each
. Thus, the
conclusion is that for each![]() the U set of
alternative solutions differs from an empty set.
the U set of
alternative solutions differs from an empty set.
3. Conclusion
In this paper we showed that:
a) it is possible to consider the problem of conflictual objectives on the line producer (increase in supply) - consumer (decrease in demand) using the mathematical economic model,
b) all contractors are responsible for balancing the unsustainable production-consumption model,
c) the compromise is achieved explicitly and accurately with regard to the decision-makers’ requirements.
References
[1] Hellwig Ż., Równowaga ekonomiczna, Pojęcie - kontrowersje, Ekonomista 1981, 3/4.
[2] Ładyga M., Tkacz M., The properties of method balancing the unsustainable production and consumption model, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 105-109.
[3] Ładyga M., Lovasova R., The method of balancing the production and consumption model in the case of indivisible goods, Polish Journal of Management Studies 2015, 11(2), 83-90.
[4] Dima I.C., Grabara J., Kolcun M., Econometric model for planning the industrial production, Journal of Applied Mathematics and Computational Mechanics 2013, 12(1), 11-20.
[5] Brzeziński S., Grabara J., Kot S., Outsourcing performance in the power plants, [in:] Elektroenergetika 2015, Proceedings of the 8th International Scientific Symposium on Electrical Power Engineering, September 16-18, 2015, Stara Lesna, Slovak Republic 2015, 28-30.

