The use of mathematical and computer modelling in solving the problems or rail transport expert examination
Nickolaj Kuzin
,Tatjana Meshcheryakova
,Oleg Kuzin
,Elena Kurileva
,Natalia Gordinskaya
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE USE OF MATHEMATICAL AND COMPUTER MODELLING IN SOLVING THE PROBLEMS OR RAIL TRANSPORT EXPERT EXAMINATION
Nickolaj Kuzin 1, Tatjana Meshcheryakova 2, Oleg Kuzin 3, Elena Kurileva 1 Natalia Gordinskaya 1
1 Lviv
Research Institute of Forensic Examinations
Lviv, Ukraine
2 Lviv branch of Dnipropetrovsk National University of Railway
Transport
Lviv, Ukraine
3 Lviv Polytechnic National University
Lviv, Ukraine
n_kuzin@mail.ru, mesherjakova.tn@gmail.com, o.a.kuzin@mail.ru
lndise@ukr.net, nvhordynska@ukr.net
Received: 27
September 2016; accepted: 11 November 2016
Abstract. The analysis of the current state of expert research of the failure of structural elements of railway rolling stock is presented. On the basis of the approaches of mechanics, mathematical and computer modeling the technique of establishing a mechanism for softening of parts and units of friction in the operation of rail transport is suggested.
Keywords: forensic examination, inverse problems of fracture mechanics, functionally gradient materials, numerical algorithms
1. Introduction. Formulation of the problem in general terms
The current state of expert research is characterized by the widespread intro- duction of the apparatus of mathematical and computer modeling in solving the problems of establishing the trace characteristics of the structural evolution and properties of parts at the time of their operation [1].
Concretization of this formulation of the problem may be different: the establishment of the causes (external and internal) that caused the realized behavior of an object, the identification of its various properties, the search evolution path of object parameters.
A characteristic feature of an expert study of railway accidents related to the destruction of elements of rolling stock structures, is the impossibility of their physical recreation. In this context, the only way to solve expert problems of establishing the causes of failure of the components is the use of mathematical models of mechanics and computer simulation techniques.
Problems that often arise in the practice of rail transport expert examinations in establishing the causes of the loss of strength parameters of structural elements of the rolling stock, namely, during the operation of rolling units, are presented in works [2, 3].
Please note that in the investigation of accidents in other transport sectors, such problems are also relevant [1]. But this time, the construction of their solution methods is open and not a completely solved scientific problem.
2. Description of the basic material. Method formulation of an expert rail transport solution
Establishing a mechanism for the softening of rolling stock parts makes it necessary to use the linked inverse problems of mechanics of deformable solids [3, 4]. Mostly, these problems are nonlinear with the presence of stochastic components, and it is almost impossible to find their analytic solution.
In this connection, in order to solve them, let us proceed from searching for the exact solution to searching for the quasi-solution according to V.K. Ivanov [5], which should satisfy the condition of:
| (1) |
where ![]() - known parameters of the object (process),
- known parameters of the object (process), ![]() - quasi-solution,
- quasi-solution, ![]() - the norm in the
corresponding metric space,
- the norm in the
corresponding metric space, ![]() - accuracy of
approximation.
- accuracy of
approximation.
Formula specification (1) can be represented as follows:
| (2) |
where ![]() - mathematical model of the process, which characterizes the railway event,
- mathematical model of the process, which characterizes the railway event, ![]() - computed approximation.
- computed approximation.
As the practice of the railway accident analysis often demonstrates the spatial and dynamic problems, the adequate choice of functional dependencies in solving them is important for such research.
The following methods of constructing the algorithms for solving equations (1), (2) have been known in literature today: Tikhonov’s regularization method, residual method, variational procedures [5].
Note that the use of these methods for solving algorithm development in 4-dimen- sional space, which includes a 3-dimensional physical space and a one-dimensional hour line, is an open problem.
To solve it, the following specification has been offered in the work of the operator representations of (1) and (2):
| (3) |
where: ![]() - time,
- time, ![]() - instants with the known conditions of
research objects,
- instants with the known conditions of
research objects,
![]() - normalizable levels of information significance.
- normalizable levels of information significance.
Expression ![]() will
be presented as follows:
will
be presented as follows:
| (4) |
As for the mathematical modeling in mechanics
problems, Euclidean spaces are most
commonly used, the norm ![]() , using the method of weighted residuals - Galerkin’s
method [5], will be presented as follows:
, using the method of weighted residuals - Galerkin’s
method [5], will be presented as follows:
| (5) |
where ![]() - significance measure of geometric locus in a body.
- significance measure of geometric locus in a body.
This expression represents an error itself used as the residual, resulting in the Galerkin’s method transformation into a method of least squares.
To illustrate the above mathematical approaches, consider the practical identification problem of material compliance at the initial time to the requirements of regulatory documents [3]. Consider the model approximation of the crack development problem in rolling stock structures, which have inhomogeneity of the property distribution, resulting from technological or operational modification.
In the case of a two-dimensional contact problem of the interaction of a rigid punch with a fragment of an elastic half-space in the area of contact interaction, we define vertical movements of the stamp, and the material fragment will be fixed along stress-free boundaries (Fig. 1).
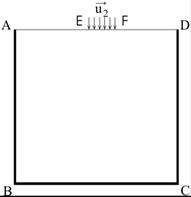
Fig. 1. Two-dimensional formulation of the problem for the material fragment (AB, BC, CD - fixing of the material fragment, EF - the area where the vertical components of the displacement vector have been defined)
The method of final element analysis (variational formulation) is used to solve the problem and is choosed the isoparametric finite element, which contains eight points (Fig. 2).
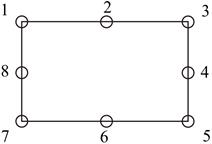
Fig. 2. Kind of the basic final element
For the purpose of detailed analysis of stress-strain state in the vicinity of the area of contact interaction, we will break it down into final elements with additional compactness directly in the zone of contact interaction, which can be set in software (Fig. 3) [6].

Fig. 3. Finite element area breakage chart (ABCD - the whole area, EFGH - a zone of tightened finite element breakage)
When solving the set problem, a program has been developed in the Maple environment. The program is searching for solutions in displacements, deformations and stresses. The work program has been examined by the test cases, which were obtained by comparing the results of numerical and analytical solutions, given in classical monographs on contact problems [6].
We assume that material mechanical properties in depth change according to the law of:
| (6) |
where: f0, f1, h - constants, which characterize the properties of the near-surface areas with known technology (operating) effects, z - depth.
In determining the trajectories of crack development in fracture mechanics, methods have been used, which can be nominally divided into two groups: the differential (stepped), which are based on local fracture criteria, and the integral (global), which are based on the criteria defined by the integrals along the sought line.
In this paper, we have used the integral fracture criterion, according to which the trajectory of crack development will be held in areas where stress satisfies the Pisarenko-Lebedev criterion relation [7]:
| (7) |
where: [R] -
critical stress level, ![]() - primary stress,
- primary stress, ![]() - maximum tensile stress,
- maximum tensile stress, ![]() - a parameter characterizing the extent
of participation in macrofracture of shearing action and is described by the
relation of: χ = Rp/Rс,
where Rс, Rp - com-
pressive resistance and ultimate resistance accordingly
(
- a parameter characterizing the extent
of participation in macrofracture of shearing action and is described by the
relation of: χ = Rp/Rс,
where Rс, Rp - com-
pressive resistance and ultimate resistance accordingly
(![]() ). For brittle
materials
). For brittle
materials ![]() , for viscous
, for viscous ![]() .
.
Suppose that at the time of measurement τ, the crack had trajectory, which is described in the model approximation, at the correlation of the physical space with the metric Euclidean space, in 2-dimensional case by the mathematical ratio.
In order
to use the apparatus of differential
calculus, we assume that ![]() , where
, where ![]() - a class of twice differentiated continuous functions.
- a class of twice differentiated continuous functions.
Set the influence of the parameter of c (toughness of material) on the trajectory of a crack development.
We find c according to the relation:
| (8) |
where ![]() - calculated crack
trajectory.
- calculated crack
trajectory.
To find solutions of parameter c, the iterative method has been used, the algorithm of which is shown in Figure 4.
If there is no such parameter c, which
satisfies the condition of ![]() , it is necessary to
use a different fracture criterion.
, it is necessary to
use a different fracture criterion.
For the numerical example, we used the change in the mechanical properties of the material in the subsurface layers of mild steel material after laser alloying. The magnitude of the contact load will be set equal to 5 MPa. Thus, with an accuracy of ε = 0.1, we accept the hypothesis about the value of the parameter of c = 0.8.
![]()
![]()
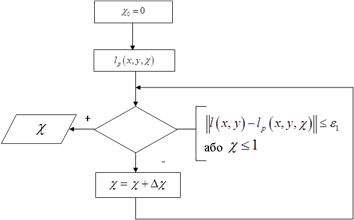
Fig. 4. Iteration algorithm of parameter χ search
The results obtained when comparing with experimental data [7] show that the state of the material in the initial time satisfied the established standards, and the cause of failure of the part are above-level loads.
3. Conclusions and prospects for further research
1. This paper introduces a method to establish the causes of failure of the structural elements of the rolling stock which operate under intense external loads.
2. The possibility of using the developed approaches in determining compliance of the mechanical characteristics to the specified values of functionally graded surface layers in conditions of external power loads has been demonstrated.
3. Further development of this technique is possible with greater ratio specificity (3)-(5), as well as with improving the model representations (7)-(8).
References
[1] McEvily A.J., Metal Failures: Mechanisms, Analysis, Prevention, John Wiley & Sons, 2002.
[2] Сокол Э.Н., Железнодорожно-транспортное происшествие и его механизм, Паїс 2011.
[3] Кузін М.О., Побудова методики ретроспективного дослідження знеміцнення залізничних конструкцій на основі фрагментарно відображеної інформації. Криминалистика и судебная экспертиза. Вып. 58, ч. 2. (Посвящается 100-летию Киевского научно-исследовательского института судебных экспертиз), 2013, с. 471-473.
[4] Bui H.D., Fracture Mechanics. Inverse Problems and Solutions, Springer, 2006.
[5] Иванова В.К., Теория линейных некорректных задач и ее приложения, Наука, 1978.
[6] Кузін М.О., Варіаційне формулювання задачі забезпечення довготривалої рівноміцності приповерхневих шарів металічних систем з врахуванням умов фрикційних навантажень. Українська академія друкарства. Наукові записки. Науково-технічний збірник 2012, № 2 (39), с. 168-172.
[7] Механические свойства конструкционных материалов при сложном напряженном состоянии, Издательский дом "Ин Юре", 2003.

