The influence of rectangular openings on the structural behaviour of sandwich panels with anisotropic core
Monika Chuda-Kowalska
,Michał Malendowski
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE INFLUENCE OF RECTANGULAR OPENINGS ON THE STRUCTURAL BEHAVIOUR OF SANDWICH PANELS WITH ANISOTROPIC CORE
Monika Chuda-Kowalska, Michał Malendowski
Institute of
Structural Engineering, Poznan University of Technology
Poznań, Poland
monika.chuda-kowalska@put.poznan.pl, michal.malendowski@put.poznan.pl
Abstract. Sandwich panels with thin metal sheets and a thick, anisotropic foam core are considered in the paper. While the experiments show a large anisotropy of core’s material, this factor is usually neglected due to elementary assemble of sandwich panels and basically simple boundary conditions. In this paper the problem of rectangular openings is considered. Thus, the influence of two main factors on the response of modelled panels are analysed, mainly: the material model of the PU foam core and openings existing in the panel. Sensitivity analysis with respect to these factors is presented. In the final part of the paper, the conclusions are formulated.
Keywords: sandwich panels, openings, soft core, anisotropic core, numerical analysis
1. Introduction
Self-supporting sandwich panels made up of two external thin and stiff metal facings separated by a thick, lightweight core are considered in the paper. These kinds of panels are widely used to cover the facades and roofs of industrial buildings. Currently, increased usage of sandwich panels is observed both for buildings’ envelope and for walls and ceilings used inside the buildings. Due to inevitable openings in the building envelope, like windows, doors or technical inlets, it is necessary to cut out holes in sandwich panels. Those openings generally have different size, geometry and locations [1] which can significantly reduce their load-bearing capacity. The European standard EN 14509 [2] specifies requirements for the production, testing and designing of complete factory-made sandwich panels, but does not include any information about openings. Thus, currently, additional support in the area of the opening in sandwich panels is required. Now, this problem is solved simply in such a way, that all applied loads on the openings are transferred by longitudinal and cross beams to the spaced frame of the building structure. Because of that, the problem of openings in sandwich panels was already undertaken in the literature and some research projects have been conducted. According to [3, 4], additional supports are not always necessary. Therefore, further research aimed at the development of consistent and appropriate design methods and testing shall be considered. Nevertheless, it is a big challenge, mainly because of the variety of factors affecting the structural response, e.g. variety of the core material, shape of the metal sheets, geometry, size and position of the openings and other issues. Although a new recommendation [5] completes the direction given in EN 14509 and introduces possibility to design sandwich panels with openings without additional support if not necessary, there are no consistent design methods, especially in case of significant size openings. In the case of a “small opening” which means that the width of the opening is smaller than the width of the plate, the resistance of the present cross-section may be sufficient.
In this work, the main attention is focused on numerical analysis of the influence of the small openings on wall sandwich panels with foam core exhibiting a large anisotropy. In most of the work, it is assumed that all layers of sandwich panels are made from homogeneous and isotropic materials. The authors proposed more advanced, orthotropic material model with nine independent constants. Testing and identified methods to obtain reliable parameters for porous material such a polyurethane foam were described in [6, 7]. The sensitivity of the structural response to variations of material parameters and the size of openings is studied and discussed.
2. Formulation of the problem
For the examined sandwich panels with a soft core, the standard experimental methods used to estimate material parameters of the core (EC, GC) are described in EN 14509. They are based on the assumption that the materials of steel facings and the core are isotropic, homogeneous and linearly elastic. The shear modulus GC of the core is identified in a four-point bending test, but Young’s modulus is deter- mined in tension/compression tests on cubic samples. In order to accurately identify the behaviour of this foam, a series of tests (tension, compression, bending) were carried out using standard procedures and a more advanced Digital Image Correla- tion (DIC) technique, named Aramis. Methods and samples were presented in detail in [6, 7]. Obtained results revealed pronounced anisotropy of the foam.
The aim of this work is to demonstrate the sensitivity of bearing capacity of sandwich panels to openings. Based on numerical studies, two material models used for the foam core are compared, with isotropic and orthotropic elasticity, based on experimentally obtained parameters. The steel sheets are modelled using standard approach with isotropic elastic properties and von Mises model of plasticity. The authors reveal that, despite the large anisotropy of the foam, to analyse the global response of the sandwich panel with soft core the application of the simplified isotropic model can be sufficiently accurate if certain conditions are met. Nevertheless, in the case of investigation of the local phenomenon, like the existence of openings in panel, a more precise description of the complex mechanical characteristics is preferred.
3. Finite element model
Structural behaviour of analysed sandwich plate with and without openings is investigated using ABAQUS simulation software package [8]. The static scheme of a system, assumed principal axes and geometrical parameters of the problem are presented in Figure 1.

Fig. 1. The scheme of the simply-supported sandwich panel with a foam core
The geometrically nonlinear static analysis is used. Geometric imperfections are introduced as a combination of five buckling modes with the multiplier 0.001 m. The problem is solved using the Newton-Raphson procedure. Numerical instability is used as failure criteria. The so-called Load Proportionality Factor (LPF) is introduced as the ratio between the load applied at the failure time to the maximum value of load artificially applied to the system. In the case of these particular analyses, LPF = 1 if the load reaches maximum value equal to 12 kN/m2. This ratio is basically introduced to make a quantitative comparison between obtained results.
The influence of frame mounted inside the opening (e.g. window frame, pipe casing) is modelled in two different ways. Firstly, the frame stiffness is neglected and only the vertical distance between corresponding nodes of lower and upper sheets is maintained. Secondly, the stiffness of the frame is introduced by additional beam element based frame, meshed in such a way, to correspond to the sheets’ mesh and be constrained to their nodes accordingly. So, from the mechanical point of view, two cases are simulated: first, neglecting the frame stiffness; second, with certain mechanical parameters of frame corresponding to actual example of frame mounted inside the opening. The former can be used arbitrarily for any frame, since that conditions result always in safe design (stiffness of the frame is neglected). The latter gives an example of a particular design situation.
3.1. Boundary conditions
Different finite elements and mesh refinements were studied to determine the most appropriate model configuration. In this paper steel faces are modelled as four node, doubly curved, thin shell, finite membrane strains elements S4 (2D element) with the size of 2 x 2 cm. The core is modelled using eight node linear brick elements C3D8 (3D element) with the size of 2 x 2 x 2 cm. S4 and C3D8 elements with full integration in stiffness computation are used in order to avoid non-physical phenomenon like hourglassing. Additionally, these elements give more accurate results in stress field for deformed elements, especially, when wrinkling phenomenon occurs. The “tie” interaction has been used between the layers, what correspond to constrained degrees of freedom of corresponding sheet and core nodes. The panel is supported by two basing plates (b = 0.1 m) modelled as rigid bodies. For the left supporting basing plate all three translations and rotations with respect to axes X and Z are equal to zero. The right basing plate differs only in that, it has the possibility of the translation in the X direction. For both basing plates free rotations with respect to the axis Y is assumed in order to obtain simply supported boundary conditions. The contact interaction between supports and sandwich panel (lower sheet) is used, with the friction coefficient equal to 0.3. The structure is loaded by uniform pressure q which is to be applied by the Newton-Raphson solver up to 12 kN/m2.
3.2. Geometry of the panel
Local instability phenomenon occurs at various supporting systems like columns and frames [9]. For sandwich panels, which are analysed in the paper, this pheno- menon is associated with short waves of buckling of the compressed face, called wrinkling. To obtain this failure mechanism it is necessary to analyse panels with a suitably chosen geometry (proportion between L/B related to D). Therefore, the following geometrical parameters are used: the total length of the system L = 3.0 m, the width B = 1.0 m and the total depth of the panel (real plate) D = 98.50 mm. The thickness of each face tF = 0.47 mm (steel + zinc) and the depth of the core dC = 97.56 mm.
The dimensions and placement of openings will be given later, when the partic- ular test cases are described.
3.3. Material parameters
In numerical analyses it is assumed that the faces are flat and made of steel and zinc with Young’s modulus EF = 195 GPa and Poisson’s ratio νF = 0.3. Moreover, the actual relationship between stress and strain is introduced. In the tensile test the obtained yield strength was equal to 360 MPa and the tensile strength reached 436 MPa. Those parameters are used for modelling the elastic and plastic properties of sheets.
The linear elastic and isotropic model of PU foam is very attractive for engineers and, it is therefore commonly used. It has only two independent constants because the relation (1) must obligatory hold in this classical model:
| (1) |
However, it appears that when E and G, identified in the tests, are introduced (Tab. 1, EZ = 5.26 MPa and GZX = 3.0 MPa, respectively) then (1) is not satisfied, because it provides negative values of the Poisson’s ratio n = –0.12. Alternatively, when the identified n and E are introduced, (Tab. 1, nZX = 0.24, EZ = 5.26 MPa, respectively) then G = 2.12 MPa obtained from (1) does not match result of experiment. This proves that the isotropic model of PU foam is inconsistent. One must be aware of this fact when using this model.
In this paper, the PU foam with a closed-cell structure and approximately 38 kg/m3 density is analysed. Material directions and coordinate system adopted in the paper are chosen based on the panel's dimensions presented in Figure 1. The experiments presented in [7] show that the analysed foam experiences evident anisotropy. The material properties of the foam core based on experimental data and used for numerical analysis are summarised in Table 1. It has to be noted, that according to code 14509 [2] only Young’s modulus in Z direction EZ (column 3) and shear modulus GZX (column 9) should be identified and used for analysis.
Table 1
Material properties of PU foam core
|
Young’s moduli [MPa] |
Poisson’s ratios [–] |
Shear moduli [MPa] |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
EX |
EY |
EZ |
nXY |
nYZ |
nZX |
GXY |
GYZ |
GZX |
|
20.04 |
4.71 |
5.26 |
0.53 |
0.17 |
0.24 |
2.51 |
2.30 |
3.00 |
|
Compression test - Aramis (DIC) |
Four-point bending test |
|||||||
In the case of the foam material model, considerations are limited to linear- -elasticity and symmetry of stress and strain tensors, and positive definiteness of the strain energy are assumed. In this case, the generalized Hooke’s law can be written in contracted engineering notation of stresses and strains as
| (2) |
where Sij is the symmetric compliance matrix. Therefore in the most general case of anisotropy Sij has 21 independent constants.
If there are two orthogonal planes of material symmetry there are only 9 independent constants and the material is termed orthotropic. In an engineering notation they are: the Young’s moduli EX, EY, EZ, shear moduli GXY, GYZ, GZX and Poisson’s ratios νXY, νYZ, νZX. The compliance matrix Sij shown in (3) is still symmetric, therefore equation (4) holds. It prescribes the relation between Poisson’s ratios nij and nji in orthogonal directions.
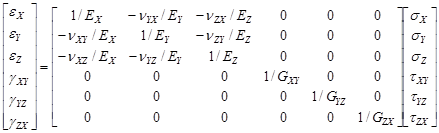 | (3) |
| (4) |
4. Numerical simulations
4.1. Sensitivity analysis with respect to material model - Example 1: panel without an opening
Because of inconsistency of isotropic material model of PU foam, the first numerical simulation is intended to demonstrate which of material parameters used in isotropic model have an influence on the structural behaviour of the sandwich plate. The analysed cases are summarised in Table 2.
In those examples, the relationships between stress and displacements in the middle of the span are obtained and presented in Figure 2.
Table 2
Numerical examples - panel without opening
|
Name of the model |
Experimental parameters of the core |
Equation (1) |
|
1 |
2 |
3 |
|
Example 1(a) |
Isotropy: E = 5.26 MPa, n = 0.24 |
G = 2.12 MPa |
|
Example 1(b) |
Isotropy: E = 5.26 MPa, G = 3.0 MPa |
n = –0.12 |
|
Example 1(c) |
Isotropy: G = 3.0 MPa, n = 0.24 |
E = 7.44 MPa |
|
Example 1(d) |
Orthotropy: 9 parameters |
Table 1 |
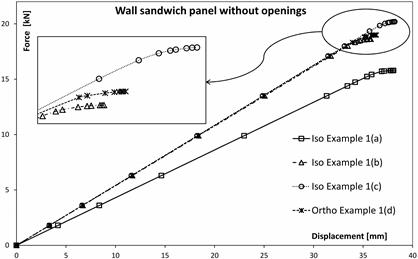
Fig. 2. FE solutions for panel without openings
Obtained results are summarised in Table 3. The column 4 represents results of wrinkling stress obtained from the numerical model. For maximum value of q (column 3) theoretical results of wrinkling stress are calculated according to equation (5) and compared with numerical results in column 6.
Table 3
Numerical examples - panel without opening
|
Name of the model |
LPF [–] |
qmax [kN/m2] |
swrFE [MPa] |
swrT [MPa] |
d [%] |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Example 1(a) |
0.439 |
5.27 |
125.7 |
120.2 |
–4.4 |
|
Example 1(b) |
0.518 |
6.22 |
140.0 |
141.7 |
1.2 |
|
Example 1(c) |
0.561 |
6.73 |
152.6 |
153.7 |
0.7 |
|
Example 1(d) |
0.528 |
6.34 |
142.3 |
144.5 |
1.5 |
For analysed case: Leff = L0 = 2.9 m, e = 0.09803 m and tF = 0.47 mm.
| (5) |
| (6) |
Paths in Figure 2 show that results obtained from Example 1(a) do not match to the other. In this case, the isotropic model with experimental values of E and n was used and the third elastic constant G was obtained from eq. (1), giving particul- arly the value of 2.12 MPa. So, reducing the shear modulus by approximately 30% (experimental value is 3.0 MPa) significantly increases the displacements. Thus, it is concluded that in an isotropic model of the foam core in sandwich panels, the shear modulus is responsible for linear path. Therefore, it plays crucial role and the actual value of this parameter must be preserved.
Example 1(b) represents the isotropic model with actual values of E and G, while Example 1(c) represents the isotropic model with experimental values of G and n. Finally, Example 1(d) represents the orthotropic model with compliance matrix (3) corresponding to the actual stress-strain relationship of material in its elastic range in three directions. Figure 2 shows exactly that for model with actual values of shear modulus G, the structural response of modelled panel is almost identical.
For higher load levels, the plots reveal the non-linearity of the structural response and different moment of failure can be observed. Analysing the results of LPF factor, column 2 in Table 3 - Example 1(b-d), it can be concluded that lower value of foam’s E causes faster local instability of the compressed face. Similar observations have been made in the paper [10].
4.2. Examples 2 and 3: panels with rectangular opening
Two different sizes of openings are studied. In the first case (Fig. 3a), named Example 2, a hole is 2 x 2 cm. Practically, the size of this opening corresponds to technical inlets. The exact location of the opening is described by following parame- ters: L1 = 0.50 m, L0 = 0.02 m, B1 = 0.49 m, B0 = 0.02 m (according to Figure 1). In this case the failure mode is similar to the panel without openings (wrinkling in the middle of the span - Fig. 3a). In the second case, named Example 3, the opening is 30 x 50 cm and its location is described by: L1 = 0.50 m, L0 = 0.50 m, B1 = 0.25 m, B0 = 0.50 m. Here, the wrinkling occurs in the vicinity of the hole (Fig. 3b). Both of the analysed openings are classified as a “small openings” because the width of the hole is smaller than the width of the plate [5].
|
a) Example 2 |
|
|
b) Example 3 |
|
Fig. 3. The first mode of the imperfection in panels with: a) opening 2 x 2 cm, b) opening 30 x 50 cm
The same four cases of the material models of the foam core are considered, as in subsection 4.1 (Tab. 2, column 1-2), but now the name is changed into “Example 2(a-d)” for panel with 2 x 2 cm opening and “Example 3(a-d)” for panel with 30 x 50 cm opening. Obtained results are summarised in Table 4.
According to relationship between Cases (a-d) for Examples 2 and 3, it can be seen, that they are similar to Example 1 e.g. model (a) manifests the lowest value of LPF factor, but models (b) and (d) are very similar. This means that the analyzed mechanical parameters and material models of the foam core have a similar effect on the panels with and without openings.
To compare results obtained from Example 1 and Example 2 it can be seen, that very small openings, like inlets, have a negligible effects on the behaviour of the structure. However, bigger openings, like in Example 3, can significantly change the failure mode and drastically reduce the load-bearing capacity of the whole panel, as shown in column 6 in Table 4.
Table 4
Numerical results - panels with and without opening
|
Name of the model |
Experimental parameters of the core |
Example |
d(a/c) [%] |
||
|
1 |
2 |
3 |
|||
|
LPF [–] |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Case (a) |
Isotropy: E = 5.26 MPa, n = 0.24 |
0.439 |
0.436 |
0.347 |
26.51 |
|
Case (b) |
Isotropy: E = 5.26 MPa, G = 3.0 MPa |
0.518 |
0.514 |
0.402 |
28.86 |
|
Case (c) |
Isotropy: G = 3.0 MPa, n = 0.24 |
0.561 |
0.558 |
0.430 |
30.47 |
|
Case (d) |
Orthotropy: 9 parameters - Table 1 |
0.528 |
0.525 |
0.407 |
29.73 |
To sum up, two parameters of the foam core have a significant impact in the analysis, both for isotropic and orthotropic models of material: the shear modulus GZX, which influences the deflection, and Young’s modulus EZ, which decides about the value of LPF. Therefore, cases (b) and (d) give similar results from the engineering point of view and they seem to be the most appropriate for modelling sandwich panel behavior and load bearing capacity.
4.3. Example 4: panels with rectangular opening and aluminium frame
In the last case, the influence of a window frame on structural behaviour of the whole panel is analysed and discussed. Because the frame is always mounted into an opening and affects the response of the system, appropriate simulations are conducted. At present, aluminium frames are commonly used for these purposes, therefore, this kind of frame is placed into the opening and analyses are carried out. As mentioned earlier, the frame is modelled using beam elements. The frame with following parameters is chosen: the cross-section A = 0.0001 m2, moments of inertia Iy = 0.000001 m4 and Iz = 0.0000005 m4, Young’s modulus E = 70 GPa and shear modulus G = 26 GPa. Taking into account findings from previous studies, only cases (b) and (d) are considered.
Failure mode obtained for panels with window frame (Example 4) shows similarity to the failure mode obtained in example without frame (Example 3). In both cases wrinkling occurs in the upper, compressed face (Fig. 4). Comparison between currently analysed Example 4, with frame mounted into opening, and Example 3 (without this frame) is presented in Figure 5. The paths 4(b) and 4(d) are almost the same (the differences are smaller than 2% - Tab. 5 - d2) which confirms the earlier findings about models adequacy.

Fig. 4. Wrinkling of the upper face in Example 4(d)
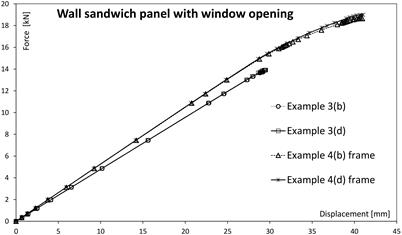
Fig. 5. Numerical paths for plate with opening 30 x 50 cm and aluminium frame
Table 5
Numerical results - panel without and with frame
|
Name of the model |
Experimental parameters of the core |
Example 3 LPF [–] |
Example 4 LPF [–] |
d1 [%] |
|
1 |
2 |
3 |
4 |
5 |
|
Case (b) |
Isotropy: E = 5.26 MPa, G = 3.0 MPa |
0.402 |
0.546 |
35.82 |
|
Case (d) |
Orthotropy: 9 parameters - Table 1 |
0.407 |
0.556 |
36.61 |
|
|
d2 [%] |
1.24 |
1.83 |
|
When Example 3 and Example 4 are compared, it can be found that the frame has significant influence on structural response of the panel. In our cases the frame increases the stiffness of the plate and improve the load capacity of the plate by more than 35% (Tab. 5, column 5).
5. Conclusions
Obtained results showed the sensitivity of the sandwich panel model to the variations of the core material model, together with parameters used in calculations, and size of the opening. In the case of a plate with an opening, introducing of the frame stiffness significantly increases the load-bearing capacity of the whole panel (35% in analysed case). It means, that the frame plays a crucial role in the response of the system. Nevertheless, neglecting the frame stiffness during design places us on the safe side. The isotropic material model could be a good approximation of the PU foam when the global sandwich panel behaviour is investigated both for panels with an opening and without an opening. Nevertheless, the shear modulus and Young’s modulus are crucial parameters in material description, since the former is responsible for appropriate computation of load-deflection path, while the later decides about failure of the entire system.
References
[1] Berner K., Pfaff U., Openings in sandwich panels, Institute for Sandwich Technology, Mainz 2005.
[2] EN 14509 Self-supporting double skin metal faced insulating panels - Factory made products - Specifications.
[3] Böttcher M., Lange J., Sandwich panels with openings, Composite Construction in Steel and Concrete 2006, 186(14), 137-146.
[4] Davis J.M., Hassinen P., Heselius L., Misiek T., ECCS/CIB Joint Committee on Sandwich Constructions: Recent European Recommendations on Design and Testing. Proceedings: W056 - Special Track 18th CIB World Building Congress, Salford, UK, 2010.
[5] Berner K., Hassinen P., Heselius L., Izabel D., Käpplein S., Lange J., Misiek T., Rädel F., Tillonen A., Zupancic D., New European recommendations for the design and application of sandwich panels - Results of the work of the Joint Committee on Sandwich Constructions, Steel Construction 2013, 6(4), 294-300.
[6] Chuda-Kowalska M., Garstecki A., Experimental study of anisotropic behavior of PU foam used in sandwich panels, Steel and Composite Structures 2016, 20(1), 43-56.
[7] Chuda-Kowalska M., Urbaniak M., Orthotropic Parameters of PU Foam Used in Sandwich Panels, Chapter IV In: Continuous Media with Microstructure 2, eds. B. Albers, M. Kuczma, Springer International Publishing, 2016, 343-353.
[8] Dassault Systemes, Abaqus Documentation, 2014.
[9] Sokół K., Uzny S., Instability and vibration of multi-member columns subjected to Euler’s load, Archive of Applied Mechanics 2016, May 86, (5), 883-905.
[10] Pozorska J., Pozorski Z., The influence of the core orthotropy on the wrinkling of sandwich panels, Journal of Applied Mathematics and Computational Mechanics 2015, 14(4), 133-138.



