Analysis of the queueing network with a random waiting time of negative customers at a non-stationary regime
Victor Naumenko
,Mikhail Matalytski
,Dmitry Kopats
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
ANALYSIS OF THE QUEUEING NETWORK WITH A RANDOM WAITING TIME OF NEGATIVE CUSTOMERS AT A NON-STATIONARY REGIME
Victor Naumenko 1, Mikhail Matalytski 2, Dmitry Kopats 1
1 Faculty of Mathematics and Computer Science, Grodno State University
Grodno, Belarus
2 Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
victornn86@gmail.com, m.matalytski@gmail.com
Abstract. In the article a queueing network (QN) with positive customers and a random waiting time of negative customers has been investigated. Negative customers destroy positive customers on the expiration of a random time. Queueing systems (QS) operate under a heavy-traffic regime. The system of difference-differential equations (DDE) for state probabilities of such a network was obtained. The technique of solving this system and finding mean characteristics of the network, which is based on the use of multivariate generating functions was proposed.
Keywords: G-network, positive customers, negative customers, random waiting time, heavy-traffic regime, state probabilities, mean characteristics, non-stationary regime
1. Network description
Consider an open G-network [1] with ![]() single-queues QS. An independent Poisson flow of positive customers with
rate
single-queues QS. An independent Poisson flow of positive customers with
rate ![]() and a Poisson flow of negative customers with rate
and a Poisson flow of negative customers with rate ![]() arrive to QS
arrive to QS ![]() from outside (system
from outside (system ![]() ),
), ![]() . All
arriving to QS customer flows are assumed to be independent. The probability
that the positive customer serviced in
. All
arriving to QS customer flows are assumed to be independent. The probability
that the positive customer serviced in ![]() during time
during time ![]() , if
at the current moment
, if
at the current moment ![]() in the system there are
in the system there are ![]() customers, are equal to
customers, are equal to ![]() .
The positive customer gets serviced in
.
The positive customer gets serviced in ![]() with
probability
with
probability ![]() move to QS
move to QS ![]() as
a positive customer and with probability
as
a positive customer and with probability ![]() - as a negative customer and with probability
- as a negative customer and with probability ![]() come out of the network to the
external environ-
ment,
come out of the network to the
external environ-
ment, ![]() .
.
A negative customer is arriving to QS increases the
length of the queue of nega-
tive
customers for one, and requires no service. Each negative customer, located
in
i-th QS, stays in the queue for a random time according to a Poisson
process of rate ![]() ,
, ![]() . By the end this
time, the negative customer destroys one positive customer in the QS
. By the end this
time, the negative customer destroys one positive customer in the QS ![]() and leaves
the network. If after this random time in
the system there are no positive customers, then a given negative customer
leaves
the
network, without exerting any influence on the operation of the network as
a whole. Wherein the probability that in QS
and leaves
the network. If after this random time in
the system there are no positive customers, then a given negative customer
leaves
the
network, without exerting any influence on the operation of the network as
a whole. Wherein the probability that in QS ![]() ,
negative customer leaves the queue during
,
negative customer leaves the queue during ![]() , on
the condition that, in this QS at time
, on
the condition that, in this QS at time ![]() there
are
there
are ![]() negative
customers, equals
negative
customers, equals ![]() .
.
The network state at time ![]() described by the
vector
described by the
vector ![]()
![]() , which forms
a homogeneous Markov process with a countable number of states, where the state
, which forms
a homogeneous Markov process with a countable number of states, where the state
![]() means that at time
means that at time ![]() in QS
in QS ![]() , there are
, there are ![]() positive
customers and
positive
customers and ![]() negative
customers,
negative
customers, ![]() . We
introduce the vectors
. We
introduce the vectors ![]() and
and
![]() ,
, ![]() - vector, which is
- vector, which is ![]() -th component equal to
1, all the others are 0,
-th component equal to
1, all the others are 0, ![]() .
.
Negative customers may describe the behavior of computer viruses, whose impact on the information (positive customers) occurs through a random time.
It should be noted that analisys at a stationary regime of QN with positive and negative customers excluding random queueing time, and also with signals has been carried out in [2, 3] and at non-stationary regime in [4, 5].
2. State probabilities of the network operating under a heavy-traffic regime
Lemma. Let ![]() - state probability
- state probability ![]() at time
at time ![]() . State probabilities of considered
network are satisfy system of DDE:
. State probabilities of considered
network are satisfy system of DDE:
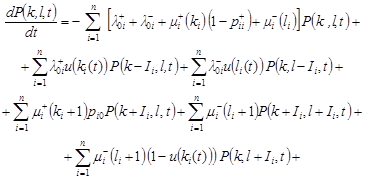 | (1) |
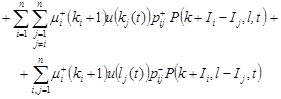 |
where ![]() ,
, ![]() .
.
Proof. The possible transitions of our Markov
process in the state ![]() during time
during time ![]() :
:
1) from the state ![]() in this case into QS
in this case into QS ![]() for the time
for the time ![]() a positive customer will arrive with probability
a positive customer will arrive with probability ![]() ,
,
![]() ;
;
2) from the state ![]() , while to the QS
, while to the QS ![]() for the time
for the time ![]() a
negative custo-
mer will arrive
with probability
a
negative custo-
mer will arrive
with probability ![]() ,
, ![]() ;
;
3) from the state ![]() , in this case the positive customer comes out of the network to the
external environment with probability
, in this case the positive customer comes out of the network to the
external environment with probability ![]() ,
, ![]() ;
;
4) from
the state ![]() , in the given case into QS
, in the given case into QS ![]() the negative customer, destroys in the QS
the negative customer, destroys in the QS ![]() the positive customer, leaves
the network; the probability of such an event is equal
to
the positive customer, leaves
the network; the probability of such an event is equal
to ![]() ,
,
![]() ;
;
5) from
the state ![]() , while in the QS
, while in the QS ![]() , the residence time in the queue of the
negative customer finished, if in time
, the residence time in the queue of the
negative customer finished, if in time ![]() there
were
there
were ![]() negative customers and there were
no positive customers; the probability of such an event is equal to
negative customers and there were
no positive customers; the probability of such an event is equal to ![]() ,
, ![]() ;
;
6) from the state ![]() , in given case after finishing the service of
the positive customer in the QS
, in given case after finishing the service of
the positive customer in the QS ![]() it moves to the QS
it moves to the QS ![]() again as a positive customer with
probability
again as a positive customer with
probability ![]() ,
, ![]() ;
;
7) from the state ![]() , in this case the positive customer, which is ser-
viced in QS
, in this case the positive customer, which is ser-
viced in QS ![]() , moves to QS
, moves to QS ![]() as a negative customer; the probability of such an event is
equal to
as a negative customer; the probability of such an event is
equal to ![]() ,
, ![]() ;
;
8) from the state ![]() , while in each QS
, while in each QS ![]() ,
, ![]() , do not arrive any positive nor any
negative customers, and in which for the time
, do not arrive any positive nor any
negative customers, and in which for the time ![]() any
customer didn’t service, no negative customer will come out of the queue; the
probability of such event is equal to
any
customer didn’t service, no negative customer will come out of the queue; the
probability of such event is equal to
![]() ,
, ![]() ;
;
9) from other states with probability
![]() .
.
Then, using the formula of total probability, we can write
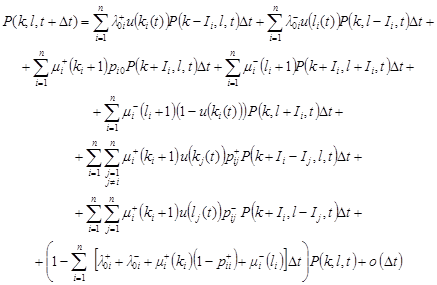 |
Taking the limit ![]() we obtain a system of equations for state probabilities
of the network. (1). The lemma is proved.
we obtain a system of equations for state probabilities
of the network. (1). The lemma is proved.
We will assume, that all queuing network
systems are single-queue, and customer
service duration in the QS has an exponential distribution with the rate ![]() . Consequently, in this case
. Consequently, in this case ![]() ,
, ![]() .
.
Denote by ![]() , where
, where ![]() , the generating
function of the dimension of
, the generating
function of the dimension of ![]() :
:
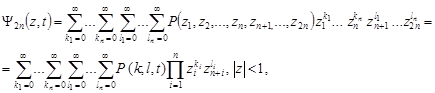 | (2) |
the summation is taking for each ![]() ,
, ![]() from
0 to
from
0 to ![]() ,
, ![]() .
.
We will assume that ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Multiplying each of the equations (1) to ![]() and summing up all possible values
and summing up all possible values ![]() and
and ![]() from
1 to
from
1 to ![]() ,
, ![]() .
Here the summation for all
.
Here the summation for all ![]() and
and ![]() is taken from 1 to
is taken from 1 to ![]() , i.e. all summands in (2), for which in
the network state
, i.e. all summands in (2), for which in
the network state ![]() there are components
there are components ![]() and
and ![]() , due to the assumptions put forward above. Because, for
example
, due to the assumptions put forward above. Because, for
example
Then we obtain
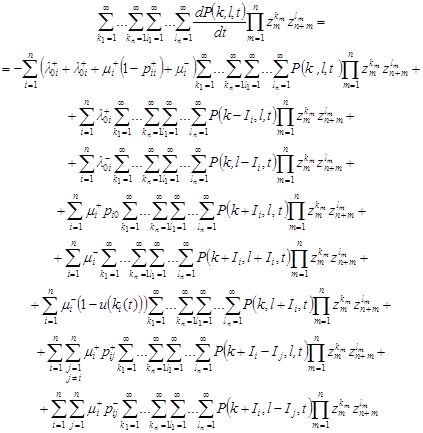 | (3) |
Let’s consider the sums, contained on the right side of the relation (3). Let
Then
Similarly for the sum ![]() we
have:
we
have:
For the sum ![]() we
obtain:
we
obtain:
The sum ![]() has
the form:
has
the form:
For the sum ![]() we
obtain:
we
obtain:
The sum ![]() .
.
For the
sum 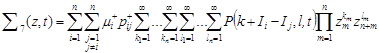 we shall obtain:
we shall obtain:
And, finally, for the last sum we shall have:
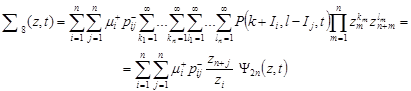 |
Using these sums, we obtain a homogeneous linear differential equation:
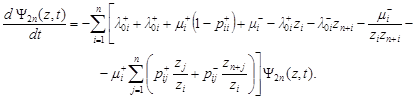 |
Its solution has the form
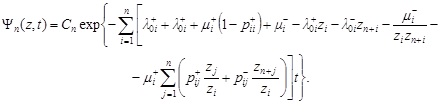 |
Let's consider, that at the initial moment of
time, the network is in a state ![]() ,
, ![]() ,
, ![]() ,
,
Then the initial condition for the last equation will be
from which we obtain ![]() .
.
Theorem. If at the initial moment of time the QN is
in a state ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
then the expression for the generating function
,
then the expression for the generating function ![]() , taking into account the expansions appearing in
it exponent Maclaurin, has the form
, taking into account the expansions appearing in
it exponent Maclaurin, has the form
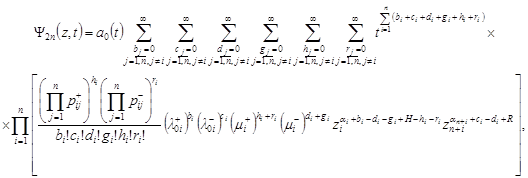 | (4) |
where
Proof. We have:
where
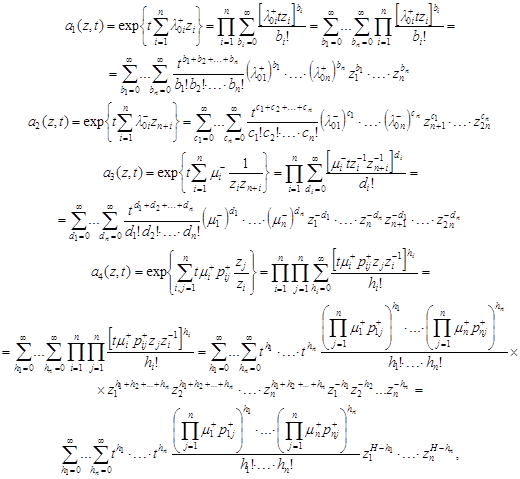 |
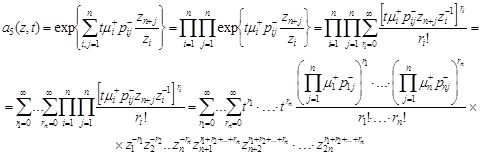 |
Multiplying ![]() ,
, ![]() , and
, and ![]() we will obtain an expression (4),
we will obtain an expression (4), ![]() .
.
State probability of ![]() is the coefficient of
is the coefficient of ![]() in the expansion of
in the expansion of ![]() in multiple series (4), with the
proviso, that at the initial time the network is in a state
in multiple series (4), with the
proviso, that at the initial time the network is in a state ![]() .
.
3. Finding the main characteristics
With the help of the generating function a
different mean network characteristics can also be found at the transient
regime. The expectation of a component with the number ![]() of
a multivariate random variable can be found, differentiating (4) by
of
a multivariate random variable can be found, differentiating (4) by ![]() and suppose
and suppose ![]() ,
, ![]() .
Therefore for the mean number of positive
customers in the network system
.
Therefore for the mean number of positive
customers in the network system ![]() we will use
the relation:
we will use
the relation:
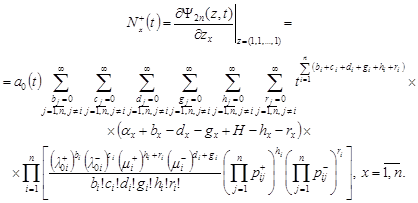 | (5) |
The change of variables will be done in the
expression (5) ![]() , then
, then ![]() and
and
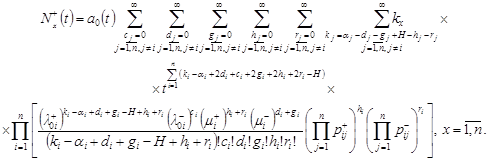 |
So like all network QS operating under
heavy-traffic regime, we obtain, then ![]() and,
consequently,
and,
consequently, ![]() , therefore
, therefore
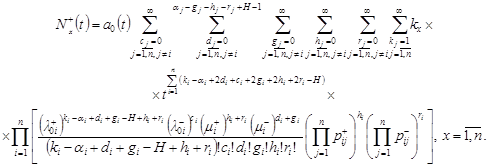 | (6) |
Similarly, we can find the relation for the
mean number of negative customers in the system ![]() ,
that are awaiting:
,
that are awaiting:
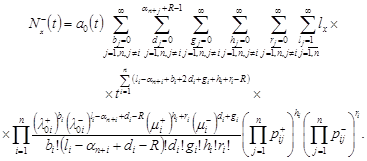 | (7) |
Example. Let the number of QS in QN be ![]() . Let external arrivals to the network of positive and negative
customers respectively equal:
. Let external arrivals to the network of positive and negative
customers respectively equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and the service times of rates equal:
, and the service times of rates equal: ![]() ,
, ![]() ,
, ![]() . Let negative customers stay in the queue
for a random time, which has an exponential distribution with parameters equal:
. Let negative customers stay in the queue
for a random time, which has an exponential distribution with parameters equal: ![]() ,
, ![]() ,
, ![]() . We assume that the transition probability of positive customers
. We assume that the transition probability of positive customers ![]() has the form:
has the form: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; transition probabilities of negative customers equal:
; transition probabilities of negative customers equal: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
then the probabilities
;
then the probabilities ![]() will be equal respectively:
will be equal respectively:
![]() ,
, ![]() ,
, ![]() . In this case
. In this case ![]() .
.
The mean number
of customers in network systems (in the queue and in servicing), on the
condition that ![]() ,
, ![]() ,
can be found by the formula (6), and the mean number of negative customers
(waiting in the queue) may be found by the formula (7).
,
can be found by the formula (6), and the mean number of negative customers
(waiting in the queue) may be found by the formula (7).
Figure 1 shows the chart of change of the
mean number of positive customers
in the QS ![]() (straight
line) and the chart of change of the mean number of negative customers (dash
line), which are awaiting in the queue of the QS
(straight
line) and the chart of change of the mean number of negative customers (dash
line), which are awaiting in the queue of the QS ![]() respectively.
respectively.
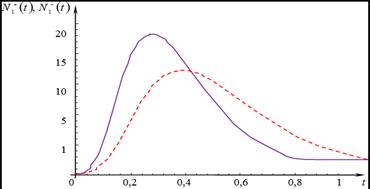
Fig. 1. The
chats of changes of the mean number of positive customers and
negative customers in the QS
![]()
4. Conclusions
In the paper, the Markov network with positive customers with a random waiting time of negative customers at transient regime has been investigated. A technique of finding non-stationary state probabilities of the above network with single-queues of QS was proposed. It is based on the method of using the apparatus of multivariate generating functions. Relations for the mean characteristics depending on time of the considered G-network, on the condition that the network operates under heavy-traffic regime was obtained.
The practical significance of these results is that they can be used for modeling the functioning of various information networks and systems, a model of which is the aforementioned network taking into account the penetration of computer viruses into it.
References
[1] Gelenbe E., Product form queueing networks with negative and positive customers, Journal of Applied Probability 1991, 28, 656-663.
[2] Gelenbe E., G-networks with triggered customer movement, Journal of Applied Probability 1993, 30, 742-748.
[3] Gelenbe Е., Pujolle G., Introduction to Queueing Networks, John Wiley, N.Y. 1998, 244.
[4] Matalytski M., Naumenko V., Non-stationary analysis of queueing network with positive and negative messages, Journal of Applied Mathematics and Computational Mechanics 2013, 12(2), 61-71.
[5] Matalytski M., Naumenko V., Investigation of G-network with random delay of signals at non-stationary behavior, Journal of Applied Mathematics and Computational Mechanics 2014, 13(3), 155-166.

