Numerical analysis of thermal processes in the system protective clothing - biological tissue subjected to an external heat flux
Bohdan Mochnacki
,Mateusz Duda
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
NUMERICAL ANALYSIS OF THERMAL PROCESSES IN THE SYSTEM PROTECTIVE CLOTHING - BIOLOGICAL TISSUE SUBJECTED TO AN EXTERNAL HEAT FLUX
Bohdan Mochnacki, Mateusz Duda
University of Occupational Safety
Management in Katowice, Katowice, Poland
bmochnacki@wszop.edu.pl, mduda@wszop.edu.pl
Abstract. The non-homogeneous fragment of biological tissue is considered. Its shape roughly corresponds to the fragment of cross-section of the upper or lower limb. The tissue domain is protected by a layer of protective clothing. The purpose of numerical computations is to examine the effectiveness of the clothing insulation layer on the action of the external heat fluxes of differing intensity. Thermal processes in the tissue domain are described by the system of the Pennes equations. This system is supplemented by the appropriate boundary-initial conditions and the energy equations determining the transient temperature field in the fabric and air gap sub-domains (the air gap is treated as a solid body). At the stage of numerical computations, the program MSC.Marc has been used. In the final part of the paper, the examples of numerical simulations and also the conclusions are presented.
Keywords: bio-heat transfer, protective clothing, tissue heating, numerical simulations
1. Introduction
Heat transfer processes proceeding in the domain of biological tissue can be described by the Fourier-type equation called the Pennes one [1-4]. The Pennes equation contains two internal source functions connected with the blood perfusion and the metabolism. The mathematical form of perfusion heat source results from the assumption that the tissue is supplied with a large number of capillary blood vessels uniformly distributed throughout its volume (a soft tissue model). The metabolic heat source can be considered in the form of a temperature-dependent function but, as a rule, is treated as the constant value.
The transient temperature field in the domain of protective clothing is determined by the Fourier equation (or in the case of multi-layered fabric by the system of these equations). In this paper the air gap (a trapped air) between the clothing and skin tissue is treated as a solid body, while the thermal conductivity of this domain is defined in a special way.
The external surface of protective clothing is subjected to the external heat flux qb [W/m2] and the different values of qb have been considered. The aim of successive numerical simulations was to determine the permissible residence times near the heat sources ensuring safe working conditions for the people at risk of burns. The acceptable times result from the temporary temperatures on the surface of the skin tissue and the internal surface of fabric.
At the stage of numerical computations, the commercial code MSC. Marc has been used.
2. Governing equations
The transient temperature field in the 2D non-homogeneous tissue domain oriented in the Carthesian co-ordinate system is described by the partial differential equations (the Pennes equations) in the form
| (1) |
where e = 1,…,4 distinguishes the tissue sub-domains, this means skin, fat, muscle and bone, respectively, ce is the volumetric specific heat, λe is the thermal conductivity, Qp,e and Qm,e are the capacities of volumetric internal heat sources resulting from the blood perfusion and metabolism, and T, x, y, t denote temperature, spatial co-ordinates and time, respectively. The perfusion heat source is given by the formula:
| (2) |
where Gb,e is the blood perfusion rate [m3 blood/(s m3 tissue)], cb is the blood volumetric specific heat and TB is the arterial blood temperature. Metabolic heat source Qm,e can be treated both as the constant value or the temperature-dependent function.
On the contact surface between the tissue sub-domains, the ideal thermal contact is assumed, namely
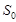 | (3) |
where ¶T/ ¶n denotes a temperature derivative in a normal direction.
The temperature field in the domain of homogeneous fabric (Tf) and air gap domain (Ta) is described by the well-known Fourier equations
| (4) |
and
| (5) |
where cf , ca are the volumetric specific heats, λf , λa are the thermal conductivities.
The problem of the air thermal conductivity requires additional explanation. The trapped air between the fabric and tissue is not moving (the convection does not occur). The heat transfer occurs by the radiation and conduction, in particular
| (6) |
where ![]() is
the radial heat transfer coefficient,
is
the radial heat transfer coefficient, ![]() is
the air thermal conductivity, while
is
the air thermal conductivity, while ![]() is
the thickness of the air gap. The total heat flux is equal to
is
the thickness of the air gap. The total heat flux is equal to
| (7) |
Now, the substitute air thermal conductivity
![]() is introduced:
is introduced:
| (8) |
or
| (9) |
wherein
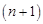 | (10) |
and
| (11) |
For example: the
mean temperatures of fabric and skin surfaces are equal to
52 and 32°C (325 and 305 K). Mean air temperature equals 42°C. For this
tem-perature thermal conductivity λa = 0.027 W/mK.
Additionally, ![]() = 0.95,
= 0.95, ![]() = 0.9 and
= 0.9 and ![]() = 0.005 m. For the above data the substitute thermal
conductivity λz = 0.057 (see Fig. 2.1). The
values of temperature-dependent air specific heat and mass density can be found
in tables (e.g. [5]).
= 0.005 m. For the above data the substitute thermal
conductivity λz = 0.057 (see Fig. 2.1). The
values of temperature-dependent air specific heat and mass density can be found
in tables (e.g. [5]).
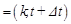
Fig. 2.1. The substitute thermal conductivity λz in temperature relation
Between the fabric, air gap and skin sub-domains, the boundary condition (3) is assumed, while between blood vessels and tissue the Robin condition is taken into account
| (12) |
where αB is the heat transfer coefficient, TB is the blood temperature. The value of αB has been found under the assumption that the Nusselt number for blood vessels is equal to 4 [6], the values of arterial and vein temperatures values have been accepted intuitively. The problem of thermal interactions between blood vessels and soft tissue is considered in the case of the so-called vessel models applications (e.g. [7]) and will not be discussed here.
The initial conditions are also given:
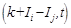 | (13) |
At the stage of numerical computations, the initial temperatures in domains of fabric and air gap have been assumed as the constant values. It is also possible to introduce the initial temperature distribution resulting from the solution corresponding to the steady state problem solved for the assumed set of external parameters [4].
3. Numerical solution of the problem
The considered domain is shown in Figure 3.1. It presents the repeatable segment of a circular cross-section containing the successive tissue layers in a sequence typical for limbs anatomy [8, 9]. Assumed dimensions of sub-regions approximately correspond to the forearm section. Taking into account the geometrical and thermal symmetry of the segment considered, on the left and right boundaries of the model the no-flux conditions can be accepted. One may notice that the layers corresponding to protective clothing and trapped air are also taken into account.


Fig. 3.1. Left: The domains of human limb secured by protective clothing. Right: The temperature response [°C] of human forearm exposed to the non-hazardous environmental conditions. The domains of fabric and air gap have been disabled from the results visualisation
Physical parameters of human tissue were taken from the paper [9]. The parameters of air and protective clothing (Cotton/Spandex) have been generated based on the online calculator [10] using the information collected in [5, 11-13]. The courses of the fabric thermal conductivity lf [W/mK] and the specific heat Cf [J/kgK] in relation to temperature [°C] are shown in Figures 3.2 and 3.3 (the mass density of fabric is equal to r = 365 kg/m3).
At the first stage of computations, the initial condition for tissue domain has been determined for the non-hazardous ambient temperature Ta0 = 20oC (heat transfer coefficient a = 3 W/m2K). The solution corresponding to the steady state conditions is shown in Figure 3.1 and it is the starting point for further computations.
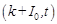
Fig. 3.2. The conductivity l of Cotton/Spandex protective clothing in relation to temperature
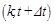
Fig. 3.3. The heat capacity cp of Cotton/Spandex protective clothing in relation to temperature
4. Results of computations
The external heat fluxes ![]() from the range [900, 2100 W/m2] warm the
external face of the fabric at the second stage of
computations. The results below presented correspond to
points A and B marked in Figure 3.1. The heat is transferred by a layer of
protective clothing and trapped air to the biological tissue. The border
temperature when the burn of tissue could occur is assumed on the different
level depending on the authors, i.e. 42oC [14], 44oC [15]
(temperature between epidermis and dermis). To estimate the burn degree the
residence time at this temperature
is essential (Henriques integral [3]). The permanent damage of biological
tissue (destruction of human protein) occurs when the temperature reaches 55°C.
In this study, the border temperature was established as 40oC due to
the fact that not only
the temperature of biological tissue should be taken into account but also the
tem-perature of the internal surface of the fabric layer - the heated
protective clothing could indirectly cause the burns, too.
from the range [900, 2100 W/m2] warm the
external face of the fabric at the second stage of
computations. The results below presented correspond to
points A and B marked in Figure 3.1. The heat is transferred by a layer of
protective clothing and trapped air to the biological tissue. The border
temperature when the burn of tissue could occur is assumed on the different
level depending on the authors, i.e. 42oC [14], 44oC [15]
(temperature between epidermis and dermis). To estimate the burn degree the
residence time at this temperature
is essential (Henriques integral [3]). The permanent damage of biological
tissue (destruction of human protein) occurs when the temperature reaches 55°C.
In this study, the border temperature was established as 40oC due to
the fact that not only
the temperature of biological tissue should be taken into account but also the
tem-perature of the internal surface of the fabric layer - the heated
protective clothing could indirectly cause the burns, too.

Fig. 4.1. The heat response of human skin exposed on different heat flux in time relation. Point B from Figure 3.1

Fig. 4.2. The heat response of fabric (internal surface - point A) exposed on different heat fluxes in time relation

Fig. 4.3. Example of results: the temperature
response [°C] of human forearm exposed
to heat flux (![]() = 1500 W/m2; t
= 282 s and t = 324 s). Corresponding domains
to the fabric and air gap have been turned off from
results visualisation
= 1500 W/m2; t
= 282 s and t = 324 s). Corresponding domains
to the fabric and air gap have been turned off from
results visualisation
5. Conclusions
The first or second
degree burn occurs when the heat penetration reaches
the dermis region. The time of hazardous
temperature appearance (e.g. 40°C)
in the above region is the different one, of course. In the case of the highest
value of heat flux ![]() = 2100 W/m2 the critical
time is equal to 240 s, while the lowest value of heat flux
= 2100 W/m2 the critical
time is equal to 240 s, while the lowest value of heat flux ![]() = 900 W/m2 this time is equal
to 360 s. The difference of
2 minutes shows the influence of the heat flux level on the heat penetration
process. The high temperatures of tissue could lead not only to burns, but also
to the heat stroke (excessive accumulation of heat in body caused by intense
influx from the environment with a difficult outflow to the environment at the
same time).
The temperature when the heat stroke occurs is equal to 43oC [16, 17]
but it should be noticed that the high temperature should appear in the
considerable parts
of tissue subdomains. This can cause an increase of
the blood temperature
which leads directly to overheating of the whole body. The protective clothing
has, as a rule, the layered structure and the
introduction of the fabric heterogeneity to the computer program is
quite easy and uncomplicated.
= 900 W/m2 this time is equal
to 360 s. The difference of
2 minutes shows the influence of the heat flux level on the heat penetration
process. The high temperatures of tissue could lead not only to burns, but also
to the heat stroke (excessive accumulation of heat in body caused by intense
influx from the environment with a difficult outflow to the environment at the
same time).
The temperature when the heat stroke occurs is equal to 43oC [16, 17]
but it should be noticed that the high temperature should appear in the
considerable parts
of tissue subdomains. This can cause an increase of
the blood temperature
which leads directly to overheating of the whole body. The protective clothing
has, as a rule, the layered structure and the
introduction of the fabric heterogeneity to the computer program is
quite easy and uncomplicated.
Acknowledgements
This work is supported by the project No. PB3/2013 sponsored by WSZOP Katowice.
References
[1] Pennes H.H., Analysis of tissue and arterial blood temperatures in the resting human forearm, J. Appl. Physiol. 1948, 1, 93-122.
[2] Majchrzak E., Mochnacki B., Dziewonski M., Jasinski M., Numerical modeling of hyperthermia and hypothermia processes, [in:] Computational Materials Science, PTS 1-3 Book Series: Advanced Materials Research, vol. 268-279, 2011, 257-262.
[3] Majchrzak E., Mochnacki B., Jasinski M., Numerical modeling of bioheat transfer in multi-layer skin tissue domain subjected to a flash fire, Computational Fluid and Solid Mechanics 2003, 1-2, 1766-1770.
[4] Ciesielski M., Mochnacki B., Application of the control volume method using the Voronoi polygons for numerical modeling of bio-heat transfer processes, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 927-935.
[5] Szargut J., Thermodynamics, Wydawnictwo Naukowe PWN, Warszawa 2000 (in Polish).
[6] Majchrzak E., Mochnacki B., Tarasek D., Dziewonski M., The BEM-FDM model of thermal processes proceeding in the domain of human finger, Acta of Bioengineering and Biomechanics 2015, 17, 4, 85-96.
[7] Majchrzak E., Application of different variants of the BEM in numerical modeling of bioheat transfer problems, MCB: Molecular & Cellular Biomechanics 2013, 10, 3, 201-232.
[8] Sinelnikov R.D., Atlas of Human Anatomy, Mir Publisher, Moscow 1996.
[9] Mochnacki B., Duda M., 3D model of thermal interactions between human forearm and environment, Journal of Applied Mathematics and Computational Mechanics 2015, 14, 3, 17-23.
[10] http://www.wolframalpha.com/ [online access 12.12.2015].
[11] Tsilingiris P.T., Thermophysical and transport properties of humid air at temperature range between 0 and 100°C, Energy Conversion and Management 2008, 49, 1098-1110.
[12] Sangsoo Lee et al., Heat and mass transfer in a permeable fabric system under hot air jet impingement, Proceedings of the International Heat Transfer Conference IHTC14, August 8-13, 2010, Washington, USA.
[13] Onofrei E. et al., Analysis of moisture evaporation from underwear designed for fire-fighters, AUTEX Research Journal 2015, 15, 1, 35-37.
[14] Barczyński M., Oparzenia, Domowy Poradnik Medyczny, PZWL 2016, online available www.medonet.pl
[15] Kutlu B., Cireli A., Thermal analysis and performance properties of thermal protective clothing, Fibres & Textiles in Eastern Europe 2005, 13, 3, 58-62.
[16] Sawicki T., Czynniki zagrażające bezpieczeństwu strażaków w warunkach pożaru, Bezpieczeństwo Pracy 2004,7-8, 35-38.
[17] Hadryś D., Occupational hazards in welding processes with micro-jet cooling, [w:] Warunki środowiska pracy, a zdrowie pracowników, red. I. Romanowska-Słomka, J. Szczurowski, Wydawnictwo Uczelniane Państwowej Wyższej Szkoły Zawodowej im. Angelusa Silesiusa, Wałbrzych 2015.

