Elastic analysis of polymeric cylinders reinforced with carbon nanotubes
Hadi Hosseini
,Reza Kolahchi
,Mohammad Mehdi Heydari
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
ELASTIC ANALYSIS OF POLYMERIC CYLINDERS REINFORCED WITH CARBON NANOTUBES
Hadi Hosseini, Reza Kolahchi, Mohammad Mehdi Heydari
Department of Civil Engineering, Khomein
Branch, Islamic Azad University
Khomein, Iran
r.kolahchi@gmail.com
Abstract. In this work, stress analysis of a polymeric cylinder’s cylindrical shell reinforced with carbon nanotubes (CNTs) is investigated. The cylinder is subjected to mechanical and thermal loadings. All the equivalent mechanical and thermal properties of nano-composite cylinder are obtained using Mori-Tanaka model. Based on equilibrium, the governing equation is derived. Using an exact solution, the stresses and radial displacement distributions in the structure are calculated. The effects of CNTs volume percent on the stresses and radial displacement for internal and external pressure cylinder are the main discussion of this study. Numerical results indicate that with increasing CNTs volume percent, the stresses decrease. However, this shows the important effect of nanotechnology in stress reduction of cylinder which may be useful in sensors and actuators.
Keywords: CNT, cylinder, elastic analysis, Mori-Tanaka model
1. Introduction
Composites offer advantageous characteristics of different materials with qualities that none of the constituents possess. Nano-composites developed in recent years have received much attention amongst researchers due to provision of new properties and exploiting unique synergism between materials. It has therefore been found multiple applications of nanocomposites in a wide range of industries including oil and gas, petrochemical, wire and cable, electronics, automotive, and construction.
Stress analysis of structures has been done by many researchers. Mechanical and thermal stresses in a functionally graded hollow cylinder were investigated by Jabbari et al. [1]. Analysis of the thermal stress behavior of functionally graded hollow circular cylinders was presented by Liew et al. [2]. You et al. [3] presented elastic analysis of internally pressurized thick-walled spherical pressure vessels of functionally graded materials. Dai et al. [4] studied exact solutions for functionally graded pressure vessels in a uniform magnetic field. Coupled thermoelasticity of functionally graded cylindrical shells was developed by Bahtui and Eslami [5]. Recently Ghorbanpour Arani et al. [6] investigated the effect of material in-homoge- neity on electro-thermo-mechanical behaviors of functionally graded piezoelectric rotating shaft. Also, they [7] studied electro-thermo-mechanical behaviors of FGPM spheres using analytical method and ANSYS software.
With respect to developmental works on analysis of the cylinders, it should be noted that none of the research mentioned above have considered composite structure and their specific characteristics. Singh and Darip [8] analyzed nonlinear vibration of composite skew plate using a four-noded shear flexible quadrilateral high precision plate bending element. Nonlinear free vibration analysis of laminated composite skew thin plates was reported by Malekzadeh [9] using DQM. Qu et al. [10] employed Rayleigh-Ritz method for vibration analyzing of a damaged piezoelectric composite plate with different boundary conditions. Zhang et al. [11] presented a three-dimensional layerwise differential quadrature (DQ) method to analyze the linear laminated piezoelastic composite plates with different materials and boundary conditions. Thinh and Ngoc [12] carried out static behavior and vibration control of piezoelectric cantilever composite plates and comparison with experiments using FE method based on the first-order shear deformation theory. Using FE method, free vibration of laminated piezoelectric composite plates based on an accurate theory was studied by Shu [13]. Using Galerkin method, Shooshtari and Razavi [14] introduced a closed form solution for linear and nonlinear free vibrations of simply supported composite and fiber metal laminated rectangular plates based on the first order shear deformation theory. Nonlinear free vibration of geometrically piezoelectric laminated composite plate was studied by Dash and Singh [15] in the Green-Lagrange sense. Electro-thermo-mechanical nonlinear vibration and instability of a fluid conveying smart composite microtube made of polyvinylidene fluoride (PVDF) were investigated by Ghorbanpour Arani et al. [16] based on the modified couple stress theory and Timoshenko beam model.
In this work, volume percent of CNTs effect is studied on thermo-elastic analysis of nano-composite cylinders. The cylinder is subjected to mechanical and thermal loads. The governing equation is solved analytically for obtaining the stresses and radial displacement.
2. Governing equations
The components of displacement are assumed as
| (1) |
The equation of equilibrium is
| (2) |
where ![]() is the stress tensor. The corresponding constitutive relations
may be written as [17]
is the stress tensor. The corresponding constitutive relations
may be written as [17]
| (3) |
| (4) |
where radial and circumferential strains are therefore reduced to
| (5) |
| (6) |
Furthermore, the temperature distribution may be written as [17]
| (7) |
To develop the analytical solution, the following dimensionless quantities are introduced:
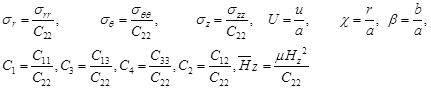 | (8) |
Using these notations and analytical method based on [17] yields the following in-homogeneity ordinary differential equations:
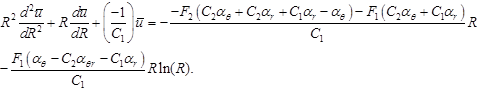 | (9) |
Equation (9), a non-homogeneous second-order ordinary differential equation, is the governing (constitutive) equation for displacement of the structure subjected to axisymmetric thermo-mechanical. The corresponding general solution for the homogeneous differential equation can be written as
| (10) |
in which ![]() and
and ![]() are integration constants to be determined by the boundary
conditions.
are integration constants to be determined by the boundary
conditions. ![]() and
and ![]() are the roots of the corresponding
characteristic equation
of Eq. (9) and may be evaluated from
are the roots of the corresponding
characteristic equation
of Eq. (9) and may be evaluated from
| (11) |
The particular solution for Eq. (9) is assumed to have the form
| (12) |
where
| (13) |
| (14) |
where
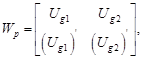 | (15) |
| (16) |
Finally, the radial displacement is
| (17) |
Substituting ![]() from
Eq. (17) into Eqs. (3) and (4), expressions for radial and circumferential
stresses can be obtained. The boundary
conditions for each case can be written as follows:
from
Eq. (17) into Eqs. (3) and (4), expressions for radial and circumferential
stresses can be obtained. The boundary
conditions for each case can be written as follows:
| | (18) |
3. Mori-Tanaka model and agglomeration effects
In this section, the effective modulus of the
composite shell reinforced by CNTs is developed. Different methods are
available to estimate the overall properties
of a composite [18]. Due to its simplicity and accuracy even at high volume
fractions of the inclusions, the Mori-Tanaka method [18] is employed in this
section. To begin with, the CNTs are assumed to be aligned and straight with
the dispersion of uniform in the polymer. The matrix is assumed to be elastic
and isotropic, with the Young’s
modulus ![]() and the Poisson’s ratio
and the Poisson’s ratio ![]() . The constitutive relations for a layer of the composite
with the principal axes parallel to the r, θ and z
directions are [18]:
. The constitutive relations for a layer of the composite
with the principal axes parallel to the r, θ and z
directions are [18]:
 | (19) |
where ![]() are the stress components, the strain components and the
stiffness coefficients, respectively. According to the Mori-Tanaka method
the stiffness coefficients are given by [18]:
are the stress components, the strain components and the
stiffness coefficients, respectively. According to the Mori-Tanaka method
the stiffness coefficients are given by [18]:
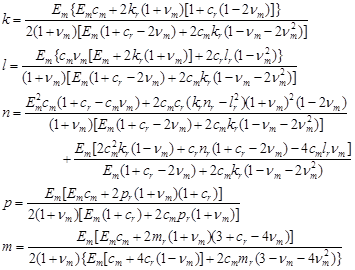 | (20) |
where ![]() and
and ![]() are the volume
fractions of the matrix and the CNTs, respectively, and kr, lr, nr, pr, mr are the Hills elastic modulus for the CNTs [15].
are the volume
fractions of the matrix and the CNTs, respectively, and kr, lr, nr, pr, mr are the Hills elastic modulus for the CNTs [15].
4. Numerical results and discussion
In this section, the stress and radial displacement distribution are plotted for different values of CNT value percent.
Figure 1
illustrates the effect of volume percent of CNTs ![]() on the radial stress of nano-composite cylinder. This
figure indicates clearly that the volume percent of CNTs has a major effect on
the radial stress. As can be seen, the radial stresses at the internal and external
surfaces of the cylinder satisfy the given boundary conditions. Moreover, an
increase in volume percent of CNTs results
in increasing radial stress.
on the radial stress of nano-composite cylinder. This
figure indicates clearly that the volume percent of CNTs has a major effect on
the radial stress. As can be seen, the radial stresses at the internal and external
surfaces of the cylinder satisfy the given boundary conditions. Moreover, an
increase in volume percent of CNTs results
in increasing radial stress.
|
|
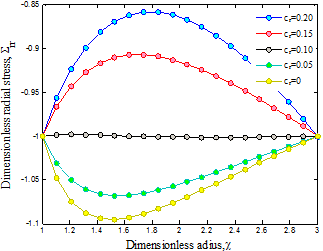
Fig. 1. Volume percent of CNT on the radial stress of structure
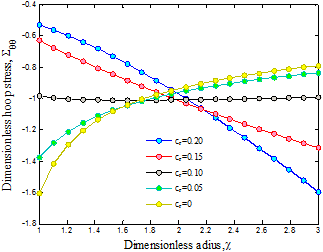
Fig. 2. Volume percent of CNT on the hoop stress of structure
The
distributions of the hoop and effective stresses for different values of ![]() are displayed in Figures 2 and 3, where the hoop stress is increased from the
inner to the outer radius for
different values of
are displayed in Figures 2 and 3, where the hoop stress is increased from the
inner to the outer radius for
different values of ![]() . Furthermore, the hoop and effective stresses
decrease with increasing volume percent of CNTs. It is due to the fact
that with increasing volume percent of CNTs, the cross-section of cylinder
reduces and hence the more CNTs participate in load transfer.
. Furthermore, the hoop and effective stresses
decrease with increasing volume percent of CNTs. It is due to the fact
that with increasing volume percent of CNTs, the cross-section of cylinder
reduces and hence the more CNTs participate in load transfer.
|
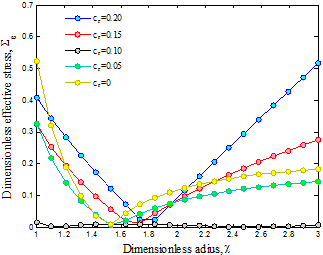
Fig. 3. Volume percent of CNT on the effective stress of structure
|
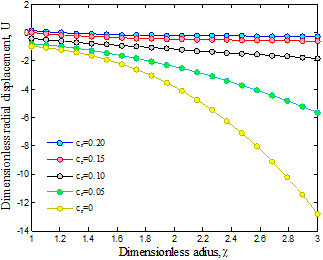
Fig. 4. Volume percent of CNT on the radial displacement of structure
The variations of the radial displacement
along the radius for different values
of volume percent of CNTs are demonstrated in Figure 4, which indicates that
the radial displacement decreases with increasing ![]() and its maximum value
occurs at the outer radius where the radial stress is maximum. It is because
that with increasing volume percent of CNTs, the stability of structure
increases and hence the radial displacement decreases. Moreover, the radial
displacement tends asymptotically to a constant value throughout the wall
thickness for
and its maximum value
occurs at the outer radius where the radial stress is maximum. It is because
that with increasing volume percent of CNTs, the stability of structure
increases and hence the radial displacement decreases. Moreover, the radial
displacement tends asymptotically to a constant value throughout the wall
thickness for ![]() .
.
5. Conclusions
Volume percent of CNTs effect on the
stresses and radial displacement
distribution of a nano-composite cylinder is the main contribution of this
work.
The Mori-Tanaka model is used for calculating the equivalent material
properties of system. An exact solution is applied for obtaining the stress and
radial displacement of cylinder. Results indicate that with increasing volume percent
of carbon nanotube, the stresses and radial displacement reduce. Moreover, the
radial displacement tends asymptotically to a constant value throughout the
wall thickness for all values of ![]() . In addition, the volume percent of
. In addition, the volume percent of ![]() is optimized
values since the distribution of stress become
constant.
is optimized
values since the distribution of stress become
constant.
References
[1] Jabbari M., Sohrabpour S., Eslamic M.R., Mechanical and thermal stresses in a functionally graded hollow cylinder due to radially symmetric loads, Int. J. Press. Ves. Pip. 2002, 79, 493-497.
[2] Liew K.M., Kitipornchai S., Zhang X.Z., Lim C.W., Analysis of the thermal stress behaviour of functionally graded hollow circular cylinders, Int. J. Solids Struct. 2003, 40, 2355-2380.
[3] You L.H., Zhang J.J., You X.Y., Elastic analysis of internally pressurized thick-walled spherical pressure vessels of functionally graded materials, Int. J. Press Ves. Pip. 2005, 82, 347-354.
[4] Dai H.L., Fu Y.M., Dong Z.M., Exact solutions for functionally graded pressure vessels in a uniform magnetic field, Int. J. Solids Struct. 2006, 43, 5570-5580.
[5] Bahtui A., Eslami M.R., Coupled thermoelasticity of functionally graded cylindrical shells, Mech. Res. Commun. 2007, 34, 1-18.
[6] Ghorbanpour Arani A., Kolahchi R., Mosallaie Barzoki A.A., Effect of material in-homogeneity on electro-thermo-mechanical behaviors of functionally graded piezoelectric rotating shaft, Appl. Math. Model. 2011, 35, 2771-2789.
[7] Ghorbanpour Arani A., Kolahchi R., Mosallaie Barzoki A.A., Loghman A., Electro-thermo-mechanical behaviors of FGPM spheres using analytical method and ANSYS software, Appl. Math. Model. 2011, 36, 139-157.
[8] Singh M.K., Darip R., Nonlinear vibration of symmetrically laminated composite skewplates by finite element method, Int. J. Non Linear Mech. 2007, 42, 1144-1152.
[9] Malekzadeh P., A differential quadrature nonlinear free vibration analysis of laminated composite skew thin plates, Thin-wall Struct. 2007, 45, 237-250.
[10] Qu G.M., Li Y.Y., Cheng L., Wang B., Vibration analysis of a piezoelectric composite plate with cracks, Compos. Struct. 2006, 72, 111-118.
[11] Zhang Z., Feng C., Liew K.M., Three-dimensional vibration analysis of multilayered piezo- electric composite plates, Int. J. Eng. Sci. 2006, 44, 397-408.
[12] Thinh T.I., Ngoc L.K., Static behavior and vibration control of piezoelectric cantilever composite plates and comparison with experiments, Comput. Mater. Sci. 2010, 49, 276-280.
[13] Shu X., Free vibration of laminated piezoelectric composite plates based on an accurate theory, Compos. Struct. 2005, 67, 375-382.
[14] Shooshtari A., Razavi S., A closed form solution for linear and nonlinear free vibrations of composite and fiber metal laminated rectangular plates, Compos. Struct. 2010, 92, 2663-2675.
[15] Dash P., Singh B.N., Nonlinear free vibration of piezoelectric laminated composite plate, Finite Elem. Anal. Des. 2009, 45, 686-694.
[16] Ghorbanpour Arani A., Abdollahian M., Kolahchi R., Nonlinear vibration of embedded smart composite microtube conveying fluid based on modified couple stress theory, Poly. Compos. 2015, 36, 1314-1324.
[17] Ghorbanpour Arani A., Kolahchi R., Mosallaie Barzoki A.A., Effect of material in-homogeneity on electromechanical behaviors of functionally graded piezoelectric rotating shaft, Appl. Math. Model. 2011, 135, 2771-2789.
[18] Mori T., Tanaka K., Average stress in matrix and average elastic energy of materials with misfitting inclusions, Acta Metall. Mater. 1973, 21, 571-574.

