Using probabilistic automata for security protocols verification
Olga Siedlecka-Lamch
,Mirosław Kurkowski
,Jacek Piątkowski
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
USING PROBABILISTIC AUTOMATA FOR SECURITY PROTOCOLS VERIFICATION
Olga Siedlecka-Lamch1, Mirosław Kurkowski2, Jacek Piątkowski1
1Czestochowa University of Technology,
Institute of Computer and Information Sciences
Częstochowa, Poland
2Cardinal Stefan Wyszynski University in Warsaw, Institute of
Computer Sciences
Warszawa, Poland
olga.siedlecka@icis.pcz.pl, m.kurkowski@uksw.edu.pl, jacekp@icis.pcz.pl
Abstract. The article discusses the issues of modeling and the analysis of executions, which is a substantial part of modern communication protocols - authentication protocols, which are generally referred to herein as security protocols. The article presents a way of security protocols executions analysis with the use of probabilistic automata, without well known and widely used perfect cryptography assumption (we assume allowing the possibility of breaking a key with a specified probability). This type of analysis leads to interesting observations about the operation of the protocol and its weaknesses.
Keywords: verification of security protocols, probabilistic methods
1. Introduction
Since the inception of the idea of security protocols for network communication a problem of verification of their correctness also exists. We want to ensure that the protocol will not only be performed, but also have guarantee of confidentiality of transmitted data, participants authentication or distribution of new session keys. There are many formal methods to check or prove if this property is assured (deductive or model checking methods). We can use many protocol specification languages (HLPSL [1], ProToc [2], CAPSL [3]), and many tools for automatic verification like AVISPA [1], VerICS [4] or PathFinder [5] (which uses the method of chains of states). However, all of those analyses and tests are made with one fundamental assumption: the assumption of perfect cryptography - the inability to decode the corresponding ciphertext without knowing the encryption key. Let's change this assumption: communication does not require the strongest keys and security, generation and implementation of which will take a lot of resources. We need to match the level of security to the level of confidentiality of communications. We can therefore investigate an acceptable probability level of an attacker compromising and runs that faster or slower result in it.
On the basis of the constructed earlier model of chains of states [6], we can generate a probabilistic automaton that models a protocol's run. We assume the existence of an Intruder, who listens, gathers information and during the run of the protocol, tries to break keys that occur during communication. This assumption meets with the well-known Dolev-Yao intruder model [7]. Everything that was previously only straight path gains branching - is expanded by a probability distribution because of the likelihood of a breaking the key of a sent message, and all keys that were used earlier - in the previous step. After adding of the probability of breaking a key and generating a model for the assumed Intruder version we can try to answer many interesting questions, for example:
- Is it profitable for the Intruder to break all the keys from the set of keys that appear during communication, or perhaps a specified subset will be sufficient to obtain complete information and make an attack or perhaps just a subset of that received full information and made an attack?
- At which level is the Intruder able to get the full knowledge and which of the keys he will have to break?
Thus, counting the total probability of reaching the particular state in the automaton, we can calculate which elements of communication require a stronger or weaker level of security.
2. Chains of states
In the following section, the idea of chains of states will be presented. As it will be shown, these chains describe all important behaviors of the system from modeling and checking point of view and can be used for formal specification of the considered protocol.
As an example, let’s consider the Wide Mouth
Frog protocol created by Burrows, Abadi and Needham [8]. The Protocol is described in so-called Common Language. In the
expressions presented below the proper symbols mean accordingly: A, B: the participants, S - server, ![]() ,
,![]() ,
,![]() : symmetric
keys, T - are timestamps.
: symmetric
keys, T - are timestamps.
We assume that the symmetric key ![]() is known only to users A and B. The scheme of the protocol’s execution is as follows:
is known only to users A and B. The scheme of the protocol’s execution is as follows:
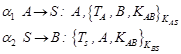 | (1) |
A sends a session key to S, including a timestamp TA. S checks that the first message is timely, and if it is, it forwards the message to B, together with its own timestamp TS. B then checks that the timestamp from S is later than any other it has received from S. The αi denotes a step of protocol. The protocol must guarantee the secrecy of the new shared key KAB: in every session, the value of KAB must be known only by the participants playing the roles of A and B and S.
The protocol must guarantee the authenticity of KAB in every session, on the reception of message in second step, B must be ensured that the key KAB in the message has been created by S in the same session on behalf of A.
In 1995, Anderson and Needham published a proposal of an attack on the Wide Mouth Frog protocol [9]:
 (2)
(2)
The
![]() denotes
i-th step of j-th execution of the protocol.
denotes
i-th step of j-th execution of the protocol.
The Intruder repeats the message from the server, so he can make the server S update the timestamp of a non-fresh key KAB. This way, he can extend the life time of a (possibly compromised) key KAB as wanted, whereas A and B think that it has expired and has been destroyed.
Now we add our model to this example. In the approach of chains of states, we define four types of states:
· states that represent specific executions of steps of the protocol.
States of this type will be determined further by: ![]() ,
where the parameter i specifies the number of step in the corresponding
execution of the protocol, and the j parameter specifies the number of
execution,
,
where the parameter i specifies the number of step in the corresponding
execution of the protocol, and the j parameter specifies the number of
execution,
· states that represent a fact of generation of confidential
information (nonces,
encryption keys) by the users. These states will be denoted by ![]() , which means generation of the secret X by user U,
, which means generation of the secret X by user U,
·
states that represent the fact of
learning the different elements of the message (which may be ciphertext) by the
receiver. These states are denoted by ![]() -
acquiring knowledge by the user U about the X,
-
acquiring knowledge by the user U about the X,
· states
representing the need of a user to have knowledge about the information
necessary to compose and send a message in the next step, those states will be
marked by![]() -
the user U must
possess knowledge about the X.
-
the user U must
possess knowledge about the X.
Using the above notation, we can represent WMF protocol as a sequence of states:
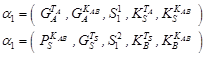 | (3) |
Now we see in detail, which information is needed (P), which generated (G) to send the message, and what is the state of the knowledge (K) of communication participants after each step (S).
The principle of operation of the protocol with chains of states can be easily visualized using deterministic automaton:
| (4) |
where:
Q is a finite set of states (chains),
Σ is a finite set of input symbols (step of protocol),
δ is a transition function: ![]() ,
,
q0 is an initial state,
F is a set of accepting (final) states ![]() (in our case
all states are final).
(in our case
all states are final).

The automata model for the Wide Mouth Frog protocol is shown in Figure 1.
In the first step user A generates the timestamp and the symetric key for a new session, and the server gains this knowledge. In the second step the server needs this generated key and generate his own timestamp. User B after the second step has the knowledge about the servers' timestamp and the symetric key KAB.
3. Probabilistic automaton
In this section we will consider situations in which there is some minimal, but a certain probability of breaking a key. For modeling the behavior and knowledge of the Intruder we will use probabilistic automaton:
| (5) |
where:
Q is a finite set of states,
Σ is a finite set of input symbols – here a power set of all keys,
δ is a transition function: ![]() ,
,
q0 is an initial state,
F is a set of accepting (final) states ![]() (in our case all states are final).
(in our case all states are final).
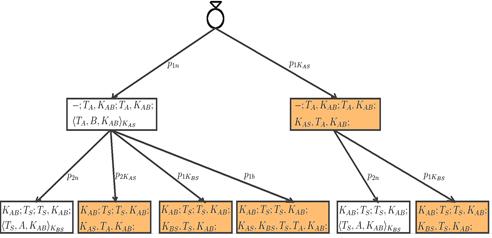
Fig. 2. PA for WMF protocol
For further analysis it is necessary to define the knowledge that the Intruder gains during the execution of the protocol. Let us denote Know(q) as knowledge of the Intruder in state q. For each path of automaton, the Intruder expands his knowledge of the transmitted ciphertext or its content - if he broke the key.
Consider the automata model for the Wide Mouth Frog protocol. The first figure (equivalent to the first and third formulas) shows in every state: the needed knowledge; generated information; gained knowledge; and knowledge of the Intruder depending on which key he broke.
Every level of automaton is connected with the concrete step of the protocol. If the Intruder didn't break the key KAS, after the first step he possesses only the ciphertext, in the other case he knows all important information (which is marked by the orange color) - timestamp and key KAB that will be used in new session. In second step, if the Intruder hadn't earlier broken the key, he will take a further attempt to break the key KAS or KBS or both, with an appropriately established probability.

Fig. 3. WMF protocol with attack
The next figure shows the situation in which the Intruder repeats the second step of the protocol (equivalent to the second formula), which gives him more time to break the keys. As shown, the Intruder is continuing only those paths on which he has not gained the full necessary knowledge - in this case: timestamp and the key for the new session. In every step the probability of breaking each of the symmetric keys grows. Some of the selected paths are preferred from the Intruder’s point of view, due to possible breaches of only one key, in the longest period of time - for example path with key KAS.
As shown in above examples, we can easily calculate the probability by the Intruder obtaining confidential information (for given values of probability of breaking respective keys).
4. Conclusions
The paper presents a new approach to analise and verify protocol safety. The use of model of chains of states allows for simple and intuitive presentation of protocols execution. It also allows to easily search for any possible attacks. However, in this model, we can go a step further by trying to match the level of security to our needs and possibilities. So we analyse not only the possibility of a standard attack, but also the probability of breaking the key. We build probabilistic automata in which we show knowledge collected by the Intruder in every step of protocol depending on, even a really small probability of breaking the given key. After constructing such automaton, we can get information about the need to strengthen or the possibility of weakening the security of some keys used by the protocol.
References
[1] Armando A. et al., The AVISPA tool for the automated validation of internet security protocolsand applications, Proc. of 17th Int. Conf. on Computer Aided Verification (CAV’05), vol. 3576 of LNCS, Springer 2005, 281-285.
[2] Kurkowski M., Grosser A., Piątkowski J., Szymoniak S., ProToc - an universal language for security protocols specification, [in:] Advances in Intelligent Systems and Computing, eds. A. Wiliński, I.E. Fray, J. Pejas, Springer Verlag 2015, Vol. 342, 237-248.
[3] Millen J., Denker G., MuCAPSL, Proc. of DISCEX III, DARPA Information Survivability Conference and Exposition, IEEE Computer Society 2003, 238-249.
[4] Kurkowski M., Penczek W., Verifying security protocols modeled by networks of automata, Fund. Inform. 2007, 79 (3-4), 453-471.
[5] Siedlecka-Lamch O., Kurkowski M., Szymoniak S., Piech H., Parallel bounded model checking of security protocols, Proc. of PPAM’13, vol. 8384 of LNCS, Springer Verlag 2014, 224-234.
[6] Siedlecka-Lamch O., Kurkowski M., Piech H., A new effective approach for modelling and verification of security protocols, Proceedings of 21th International Workshop on Concurrency, Specification and Programming (CS&P 2012), Humboldt University Press, Berlin 2012, 191-202.
[7] Dolev D., Yao A., On the security of public key protocols, IEEE Transactions on Information Theory 1983, 29(2), 198-207.
[8] Burrows M., Abadi M., Needham R., A logic of authentication, ACM Transactions on Computer Systems 1990, 8, 18-36.
[9] Anderson R., Needham R., Programming satan's computer, Computer Science Today, LNCS 1995, 1000, 426-440.

