Between syntax and semantics of resource oriented logic for IDS behavior description
Ján Perháč
,Daniel Mihályi
,Valerie Novitzká
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
BETWEEN SYNTAX AND SEMANTICS OF RESOURCE ORIENTED LOGIC FOR IDS BEHAVIOR DESCRIPTION
Ján Perháč, Daniel Mihályi, Valerie Novitzká
Department of Computers and Informatics
Faculty of Electrical Engineering and Informatics
Technical University of Košice
Košice, Slovakia
Jan.Perhac@tuke.sk, Daniel.Mihalyi@tuke.sk, Valerie.Novitzka@tuke.sk
Abstract. Linear logic appears as a suitable logical system for description of dynamic properties of various network activities in computer science. It disposes with new connectives which create new opportunities to describe properties of real network processes, e.g. parallelism, causality and commutativity of duality between processes. We extend this logic with Aristotelian modalities and we formulate their appropriate model. In our contribution we show how a real network attack can be formalized in this logical system as a polarized game.
Keywords: intrusion detection system, linear logic, Kripke’s semantics, ludics
1. Introduction
Nowadays, a computer network security is a very important aspect of any worldwide organization. Every day the attackers create new malicious software or types of attacks, so people need to protect their systems against them. Traditionally, as a protection against malicious software the anti-virus software is used. But how to protect network against network attacks? Every computer network has to be protected by administrator’s settings configured manually, another way is to do it automatically with the implementation of the network Intrusion Detection System (IDS) [1, 2].
In our experimental lab we use the open source network tool Snort. The Snort is a type of IDS [3], where intrusion detection is based on known algorithms and attack pattern, i.e. signatures.
Our approach related to formal description of network security leads to the idea how intrusion detection system behavior can be specified through resource oriented logical system’s formula [4, 5]. We model this behavior by coalgebras where IDS is modelled as a coalgebra for an appropriate polynomial endofunctor defined in the abstract frame of category theory [6]. In [5, 7] is presented linear logic [8-10] extended with epistemic modalities - epistemic linear logic for formal description how objective knowledge and rational belief can be formulated in resource-oriented formula in Kripke’s model of possible worlds through extensional satisfaction relation.
The proposed resource oriented logical system here is Modal Linear Logic (MLL) for a formal description of IDS behavior which consists of three fundamental building blocks: the language, semantics and proof system. The language introduced in [4, 5] is based on symbols of language, its syntax and properties. We differentiate a proof system to linear Gentzen’s calculus, which we define in [5], and time-spatial Gentzen’s calculus.
In this paper we extend our approach by formulating the Kripke’s semantics for the proposed logical system (MLL) through intensional satisfaction relation and then we apply logical time and space from Girard’s theory of ludics [11]. The whole process of the catching network intrusion by IDS we specify by behavioral resource oriented logical formula. In terms of ludics theory, we can consider this formula as a game, modeled by a polarized tree where resources, i.e. logical time and space, mutually alternate with respect to ordering relation defined between loci.
Firstly, we introduce the syntax, model and deduction system of resource-oriented logic with modalities for real network intrusions description. We divide the deduction system into two categories: linear proof system and time spatial proof system. Both systems are in the Gentzen’s style double side sequent forms. Finally, we demonstrate a real network intrusion example as a polarized game placed in logical time incrementation as sequential execution of clusters. Based on computer architecture, i.e. the number of CPU’s cores, we get a guideline for parallelization of the actions in the given cluster. A cluster serves as an effective tool for manipulation with CPU’s cores. Ludics addresses composed from biases abstract memory addresses of a computer where IDS is implemented. It helps us to precisely model what exactly happened in the given network segment and where it is in the IDS’s computer memory.
2. Modal linear logic
In this section we firstly introduce basic notions of linear logic and modal operators of Aristotle's modal logic. Then we introduce modal linear logic which appears to be well suited to express the possibility/necessity dynamic of particular network intrusions.
Linear logic was originally introduced as a resource-oriented logic with a stronger expressive power [8] than propositional logic based on the Tarski’s semantical tradition, thanks to introduction of the new connectives. Compared to that, a modal logic with its pleonasmic approach of dealing with formulae [12], is the logic of possibility and necessity.
In our approach we categorize linear logic connectives [4, 13, 14] together with modal operators as shown in Figure 1. There are few points of view:
· Multiplicative (intensional) fragment in the sense of Heyting’s semantical tradition depicted in the left vertical ellipse and additive (extensional) fragment in Tarski’s semantical tradition shown in the right vertical one.
· Positive fragment (diagonal ellipse from the top left corner to the bottom right one) and negative fragment (diagonal ellipse from the top right corner to the bottom left one) we understand in sense of polarization of the connectives. Here we assign polarity to modal operators based on duality of original exponentials: positive connectives in algebraic style and negative in the logical one.
·
In the horizontal ellipses is the type depicted manipulation
fragment, the top one shows the product (constructor ![]() together with projection selector
together with projection selector ![]() ) and the bottom one shows the coproduct (deconstructor
) and the bottom one shows the coproduct (deconstructor ![]() together with coprojection integrator
together with coprojection integrator ![]() ) of any two linear types.
) of any two linear types.
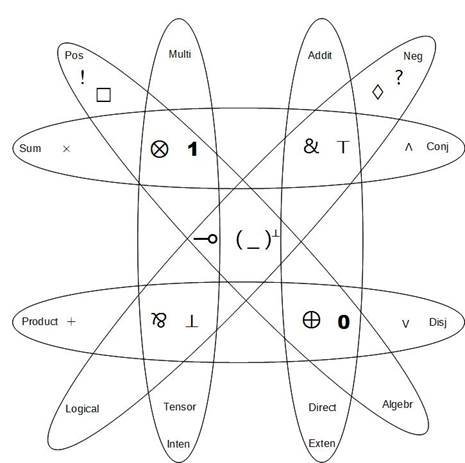
Fig. 1. Fragmentation of linear logic connectives
2.1. Language of MLL
For our approach of a formal description of the IDS, we choose a way of creating a new logical system which will suit our needs in three steps:
1. the language;
2. the semantics and
3. the proof system.
The language of modal linear logic for IDS is composed from the multiplicative fragment of linear logic and modal logic (Fig. 1). In [5], we already introduced its symbols and its syntax, then we define De Morgan’s laws for each element of the syntactical production rule (1) defined below.
1. Symbols of the MLL are:
·
elementary formulae: ![]() , where
, where ![]() ;
;
· connectives:
i.
unary: ![]() ,
, ![]() ,
, ![]() and
and
ii.
binary: ![]() ,
, ![]() ,
, ![]() .
.
·
constants: ![]() ,
, ![]() also called neutral elements for connectives
also called neutral elements for connectives ![]() ,
, ![]() respectively;
respectively;
·
formulae of MLL: ![]() ;
;
·
auxiliary symbols: brackets ![]() ,
,![]() .
.
2. Syntax of the MLL is defined by the production rule in the Backus-Naur form as follows:
![]() (1)
(1)
by
which all formulae of the MLL can be constructed. The set of all formulae of
the MLL we denote as ![]() .
.
Properties of the mentioned connectives are:
·
(Causal) linear implication : ![]() , expresses the fact
that action φ is the cause of (re)action ψ and after
performing the implication, a resource φ
becomes consumed, i.e.
, expresses the fact
that action φ is the cause of (re)action ψ and after
performing the implication, a resource φ
becomes consumed, i.e. ![]() .
.
·
Multiplicative conjunction ![]() has neutral element
has neutral element ![]() . Formula
. Formula ![]() expresses parallelism property, i.e. performing of the both actions at the same
time.
expresses parallelism property, i.e. performing of the both actions at the same
time.
·
Multiplicative disjunction ![]() has neutral element
has neutral element ![]() and it is dual connective
to the connective
and it is dual connective
to the connective ![]() . Formula
. Formula ![]() expresses dependence
between two
actions. The linear formula
expresses dependence
between two
actions. The linear formula ![]() means that if the
action
means that if the
action ![]() will be not performed,
then the action
will be not performed,
then the action ![]() will be and
vice versa. In other words, it expresses commutativity
of duality between action and reaction.
will be and
vice versa. In other words, it expresses commutativity
of duality between action and reaction.
·
Linear negation is, according to the author of
linear logic [8], the most
important connective of linear logic (shown in the middle of Fig. 1). It is
involutive (i.e. ![]() and expresses duality property
as depicted in
Table 1:
and expresses duality property
as depicted in
Table 1:
Table 1
Duality property of the linear negation
|
action |
reaction |
|
available resource |
consumed resource |
|
input |
output |
·
Unary connectives ![]() ,
, ![]() are called modalities
[12], where
are called modalities
[12], where ![]() expresses necessity action
(it could be read as: it is necessary that
expresses necessity action
(it could be read as: it is necessary that ![]() ) and
) and ![]() expresses possibility action
(it could be read as: it is possible that
expresses possibility action
(it could be read as: it is possible that ![]() ).
).
3. In the last step, we define characteristic properties of the connectives considering De Morgan’s laws in the Table 2.
Table 2
MLL De Morgan’s laws
|
|
|
|
(dm1) |
|
|
|
|
(dm2) |
|
|
|
|
(dm3) |
|
|
|
|
(dm4) |
|
|
|
|
(dm5) |
|
|
|
|
(dm6) |
|
|
|
|
(dm7) |
|
|
|
|
(dm8) |
2.2. Semantics of MLL
For the definition of modal linear logic semantics, we formulate the Kripke’s interpretation of possible worlds semantics, based on Kurz’s approach [12], because it is suitable for expressing the semantics of logic, which deals with the intension of formulae based on Heyting’s semantical tradition.
Definition 1.
Kripke’s model ![]() is ordered quadruple
is ordered quadruple ![]() , where:
, where:
·
![]() is non-empty set of
possible worlds:
is non-empty set of
possible worlds: ![]() ;
;
·
![]() is a binary
accessibility relation between worlds:
is a binary
accessibility relation between worlds: ![]()
·
![]() is intensional satisfaction
relation:
is intensional satisfaction
relation: ![]() , where
, where ![]() assigns to the
elementary formula
assigns to the
elementary formula ![]() in world
in world ![]() , a value from set:
, a value from set: ![]() , where
, where ![]() means sense and
means sense and ![]() is nonsense and
is nonsense and
·
![]() is designated world
is designated world ![]() .
.
Based on Definition 1 we construct Kripke’s model of modal linear logic for IDS as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Notation ![]() can be read as “modal
linear formula
can be read as “modal
linear formula ![]() has sense in world
has sense in world ![]() , in
model
, in
model ![]() ”.
”.
2.3. Deduction system of MLL
In this section we firstly introduce a linear proof system for our logic and then we apply the Girard’s ludics theory of time-spatial calculus.
1) Linear proof system:
In our final step of creation of the MLL, we have to define the proof system. For that, we have analyzed current options and we have chosen the Double-side Gentzen’s Sequent Calculus (DSGSC).
Deduction rules for MLL have following form:
where ![]() are finite sets of formulæ. Meaning of
are finite sets of formulæ. Meaning of ![]() is:
is:
| (2) |
and it could be read as “multiplicative disjunction of formulae in the sequent’s succedent (i.e. right side) is provable from multiplicative conjunction of formulae in the sequent’s antecedent (i.e. left side)”.
Deduction rules of the DSGSC of MLL are:
· Identity and Cut rules:
![]()
· Structural rules:
![]()
· Logical rules:
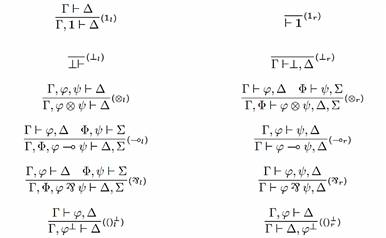
· Modal rules:

The proof of the formula is a tree and the root is the sequent where the given formula is placed. Every node (as a proof instance) of the proof tree is created by the application of an appropriate rule until every leaf becomes an axiom. The rule consists of the assumption(s) (except for axiom which has no assumption) placed above the line and conclusion placed under the line. If all these conditions are fulfilled, then a proof is constructed properly and the formula is proved.
2) Time spatial proof system:
Objects of linear logic are constructed, so all logical information in the formulae is erased, only their locations (addresses) are preserved in the peculiar locative structure that we call design. This structure is in the form of a time-spatial sequent system which is well-known as pitchfork calculus [11] that uses double sided sequents written in Gentzen’s style. A pitchfork is the expression of the form
![]() (3)
(3)
where ![]() is a singleton containing one locus, i.e. address called “handle of the pitchfork”,
is a singleton containing one locus, i.e. address called “handle of the pitchfork”, ![]() is a
finite set of loci that we call “tines of the pitchfork” and
is a
finite set of loci that we call “tines of the pitchfork” and ![]() . A pitchfork is positive if it has no handle and negative if a
handle is present.
A design is a proof tree constructed of pitchforks where the last pitchfork is
called the base. There are three rules used in building design:
. A pitchfork is positive if it has no handle and negative if a
handle is present.
A design is a proof tree constructed of pitchforks where the last pitchfork is
called the base. There are three rules used in building design:
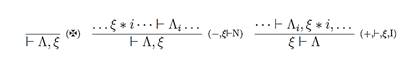
where ![]() is positive rule containing the ramification
is positive rule containing the ramification ![]() as a
set of biases
as a
set of biases ![]() .
. ![]() is negative rule that consists from directory
is negative rule that consists from directory ![]() as
a set of ramifications
as
a set of ramifications ![]() , and
, and ![]() is daemon as axiom.
is daemon as axiom.
Next we define ordering relation ![]() between loci. Two loci can be w.r.t. this
relation
between loci. Two loci can be w.r.t. this
relation
1. comparable, i.e. they are ordered and their relation is temporal or
2. incomparable i.e. they are pairwise disjoint and their relation is spatial.
In our approach the temporal relation between the loci expresses the timeline of sequential execution of particular clusters and spatial relation between the loci shows where part of the intrusion is placed in a computer memory.
3. Motivation example
For catching network intrusions in real world, we have created the laboratory environment where we have decided to use real network devices instead of the virtualization of them.
In our case for demonstration, we have simulated a so-called “man-in-the-middle” network attack (Address Resolution Protocol) ARP Spoofing attack in the lab. The principle of such an attack and the network topology of our experimental conditions are shown in Figure 2.
In [5], we have formally described the behavior of the IDS Snort during ARP Spoofing attack as resource-oriented formula MLL
| (4) |
where:
·
![]() denotes vertical
scanning of the Victim’s host ports;
denotes vertical
scanning of the Victim’s host ports;
·
![]() is activity of IDS at Attacker’s vertical scanning of the Victim’s
host ports by creating a log about a potential attack;
is activity of IDS at Attacker’s vertical scanning of the Victim’s
host ports by creating a log about a potential attack;
·
![]() means a bypass of the communication through the Attacker’s PC2 from
Victim’s PC1 to the ROUTER;
means a bypass of the communication through the Attacker’s PC2 from
Victim’s PC1 to the ROUTER;
·
![]() means a bypass of the communication through the Attacker’s PC2 from
the ROUTER to the Victim’s PC1;
means a bypass of the communication through the Attacker’s PC2 from
the ROUTER to the Victim’s PC1;
·
![]() is activity of IDS at transferring communication between the Victim’s
PC1 and the ROUTER by creating an appropriate log about the attack and
is activity of IDS at transferring communication between the Victim’s
PC1 and the ROUTER by creating an appropriate log about the attack and
·
![]() as attack.
as attack.
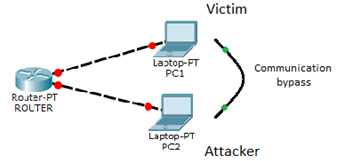
Fig. 2. Network topology and a principle of ARP spoof attack
Then we have shown its proof in linear sequent calculus as follows:
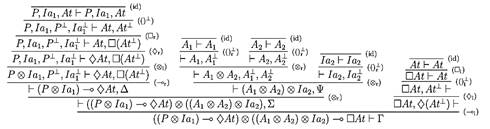
Fig. 3. Proof tree of (4) in linear sequent calculus
where:
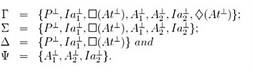
Fig. 4. Contexts used in Figure 3
The proof tree in the linear proof system depicted in Figure 3 is constructed from the root (behavioral formula) to the leaves, which are identities. Every deduction step is realized by use of an appropriate structural/logical/modal rule of the linear Gentzen’s calculus mentioned above. The whole proof tree represents the dynamic process of incoming ARP Spoofing network intrusion and IDS’s reaction to it.
Using the time-spatial proof system in Gentzen’s style [10, 11], we can depict locative structure (i.e. Designs) of treated ARP Spoofing intrusion as a polarized Böhm tree. We construct it in few steps, where first of all, we applied De Morgan’s laws introduced in Table 2 to translate the original formula (4) from the attacker point of view to a new orthogonal formula that expresses this attack from the network environment point of view as follows:
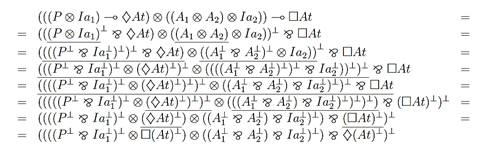
Fig. 5. Translation of (4) to De Morganized one
In every step of formula translation, we underline the appropriate part, where a particular law (dm1 - dm8) is applied. At the next steps, we use the involutive property of the linear negation repeatedly which is expressed by dm3 law.
Further, we construct an appropriate proof tree in DSGSC style, where the root of the tree is a “De Morganized” formula and every derivation step is realized by using an appropriate rule applied to obtain new proof instance. Based on equalities from Table 2, we can claim that this proof is equivalent to the proof of the original one depicted in Figure 3.
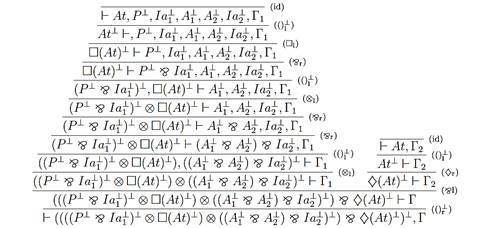
Fig. 6. Proof tree of De Morganized (4) in linear sequent calculus
where
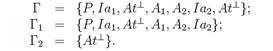
Fig. 7. Contexts used in Figure 6
The formula entailment (¯At) expresses the possibility of realizing an attacker’s vertical portscan. The formula entailment (£At) expresses the necessity of capturing harmful communication between the victim and router via attacker that we conceptualize as a specific kind of linear modalities that are the most important part of polarized game plans. These plans can be modelled as a polarized tree in sense of the time-spatial Gentzen’s calculus. Then, in linear sequent instances, we can identify clusters of polarities by using the linear negation rule. The proof step expresses individual time incrementation, here expresses the fact that application of the negation rule is causing leaping of appropriate (sub)formula between left and right side of the turnstile depicted in Figure 8. It occurs when a new cluster of the same polarity passed. The actions in a cluster can be performed simultaneously, possibly by more CPUs, depending on the particular computer architecture.
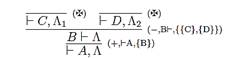
Fig. 8. Clustered proof tree of De Morganized formula (4)
where
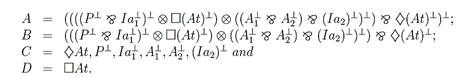
Fig. 9. Formulae substitutions used in Figure 8
Every proof step in the clustered proof tree (Fig. 8) corresponds to applying an appropriate rule of the time-spatial Gentzen’s calculus, where any logical information about original subformulae in Figure 9 is substituted by appropriate locative addresses, i.e. loci in the design shown in Figure 10.
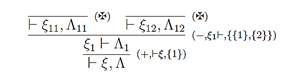
Fig. 10. Polarized proof tree of De Morganized formula (4) in time-spatial sequent calculus
where:
![]()
![]()
![]()
![]()
Finally, we obtain
the design in Figure 10 for expressing the locative structure of the network
intrusion. It consists of two time lines of comparable loci with
respect to ordering relation ![]() . The first, left one
. The first, left one ![]() represents the sense (genius of loci) of the possibility of the
vertical portscan intrusion and the second one
represents the sense (genius of loci) of the possibility of the
vertical portscan intrusion and the second one ![]() that represents the sense of necessity of the ARP Spoofing network
attack. From the spatial point of view the loci
that represents the sense of necessity of the ARP Spoofing network
attack. From the spatial point of view the loci ![]() and
and ![]() are incomparable and pairwise disjoint,
i.e.
are incomparable and pairwise disjoint,
i.e. ![]() . We can also interpret this design as the polarized game, where
linear negation depicted in the middle of Figure 1 is conductive to move
alternation between the proponent and opponent within the scope of the Böhm
tree depicted in the design (Fig. 10).
. We can also interpret this design as the polarized game, where
linear negation depicted in the middle of Figure 1 is conductive to move
alternation between the proponent and opponent within the scope of the Böhm
tree depicted in the design (Fig. 10).
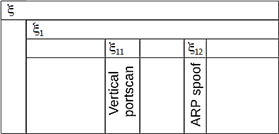
Fig. 11. Computer memory
This approach helps network administrators understand how particular network intrusion on the computer architecture (where IDS is implemented) through resources of logical system are manipulated:
· by alternation clusters as the time incrementation that can be treated sequentially (one computer processor) or simultaneously (more computer processors) and
·
by loci that are placed exactly in the locative
structure as computer memory
addresses. The main locus ![]() is the memory address where the whole network intrusion activity
was detected and subloci
is the memory address where the whole network intrusion activity
was detected and subloci ![]() ,
, ![]() where
where ![]() is the memory address of the vertical portscan activity (optional
part of network intrusion) and
is the memory address of the vertical portscan activity (optional
part of network intrusion) and ![]() is the memory address of the ARP spoof attack.
is the memory address of the ARP spoof attack.
4. Conclusions
In this contribution we demonstrate how real network intrusion can be described formally in terms of a modal resource-oriented logical system where resources were introduced in logical time and space as a polarized game whose moves are initiated by linear negation rules. We have formulated the semantics of this system in Kripke’s approach.
In the future we would like to extend our approach by applying a new resource oriented logical level related to a formal resource oriented rational belief, desire and intention of description of the rational agent obtaining knowledge about network intrusion.
Acknowledgements
This work was supported by the Faculty of Electrical Engineering and Informatics, Technical University of Košice under the contract No. FEI-2015-18: Coalgebraic Models of Component Systems.
References
[1] Vokorokos L., Baláž A., Adám N., Secure web server system resources utilization, Acta Polytechnica Hungarica 2015, 12, 2, 5-19. Available at: https://uni-obuda.hu/journal/Vokorokos_ Balaz_Adam_58.pdf
[2] Vokorokos L., Baláž A., Madoš B., Application security through sandbox virtualization, Acta Polytechnica Hungarica 2015, 12, 1, 83-101. Available at: https://uni-obuda.hu/journal/ Vokorokos_Balaz_Mados_57.pdf
[3] Ennert M., Chovancová E., Dudláková Z., Testing of IDS model using several intrusion detection tools, Journal of Applied Mathematics and Computational Mechanics 2015, 14, 1, 55-62. Available at: http://dx.doi.org/10.17512/jamcm.2015.1.05
[4] Mihályi D., Novitzká V., Towards to the knowledge in coalgebraic model IDS, Computing and Informatics 2014, 33, 1, 61-78.
[5] Perháč J., Mihályi D., Intrusion detection system behavior as resource-oriented formula, Acta Electrotechnica et Informatica 2015, 15, 3, 9-13, DOI: 10.15546/aeei-2015-0022. Available at: http://www.aei.tuke.sk/papers/2015/3/02_Perha%C4%8D.pdf
[6] Perháč J., Mihályi D., Coalgebraic modeling of IDS behavior, IEEE 13th International Scientific Conference on Informatics, November 18-20, 2015, Poprad, Slovakia, Danvers: IEEE, 2015, 201-205, DOI: 10.1109/Informatics.2015.7377833
[7] Mihályi D., Novitzká V., Ľaľová M., Intrusion detection system episteme, Central European Journal of Computer Science 2012, 2, 3, 214-220.
[8] Girard J.-Y., The Blind Spot. Lectures on Proof-theory, Institut de Mathématiques de Luminy, Marseille, France, 2011, ISBN 978-3-03719088-3.
[9] Novitzká V., Mihályi D., Slodičák V., Linear logical reasoning on programming. Acta Electrotechnica et Informatica 2006, 6, 3, 34-39. Available at: http://www.aei.tuke.sk/papers/ 2006/3/Novitzka.pdf
[10] Steingartner W., Poláková A., Prazňák P., Novitzká V., Linear logic in computer science. Journal of Applied Mathematics and Computational Mechanics 2015, 14(1), 91-100. Available at: http://dx.doi.org/10.17512/jamcm.2015.1.09
[11] Girard J.-Y., Locus solum: From the rules of logic to the logic of rules, Mathematical Structures in Computer Science 2001, 11, 3, 301-506.
[12] Kurz A., Coalgebras and Modal Logic. Lecture notes, CWI, Amsterdam 2001.
[13] Mihályi D., Novitzká V., What about linear logic in computer science? Acta Polytechnica Hungarica 2013, 10, 4, 147-160. Available at: http://www.uni-obuda.hu/journal/Mihalyi_ Novitzka_42.pdf
[14] Novitzká V., Slodičák V., On applying stochastic problems in higher-order theories, Acta Electrotechnica et Informatica 2007, 7, 3.

