Analysis of critical percolation clusters of mixtures of conducting and dielectric polymers
Andrzej Katunin
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
ANALYSIS OF CRITICAL PERCOLATION CLUSTERS OF MIXTURES OF CONDUCTING AND DIELECTRIC POLYMERS
Andrzej Katunin
Institute of Fundamentals of Machinery
Design, Silesian University of Technology
Gliwice, Poland
andrzej.katunin@polsl.pl
Abstract. The paper deals with the analysis of critical percolation clusters that have resulted from the numerical simulation of mixtures of various conducting polymers in a dielectric medium. The conducting particles in the electrical percolation problem are modelled follow- ing the hard-core/double soft-shell model which considered realistic values of particles dimensions, electrical conductivity and hopping distances. The new formulation of the chemical distance distribution in the percolation clusters is developed and several representative examples using this formulation are presented. In order to verify the fractal nature of the obtained critical percolation clusters the Minkowski-Bouligand dimension formulation was applied. Approximation of obtained results confirms the fractal nature of analysed clusters.
Keywords: electrical percolation, critical percolation cluster, chemical distance distribution, Minkowski-Bouligand dimension, conducting polymers
1. Introduction
Since Flory [1] and Stockmayer [2] have discovered the fundamentals of the percolation theory based on the studies on gelation processes in branched polymers, this theory has been intensively developed by numerous researchers in various problems until nowadays. The percolation theory has found an application in the problems related to chemistry, informatics and communications, materials, soil and fluid mechanics, and many others. This theory allows for the describing and modelling the phase transitions of jumpwise character in various physical processes as well as multi-component systems interaction and self-organization.
One of the intensively developed problems of the percolation theory is its application in electrical conductivity of materials and their composites. The percolation problems formulation can be generally classified into two groups: the percolation of nodes organized in lattices and the percolation of randomly distributed nodes. Both groups are characterized by the percolation threshold, which represents a critical point of transition when the sudden change of a system occurs. In electrical percolation problems, the percolation threshold represents the critical concen- tration of conducting particles in a dielectric medium, which causes the whole mate- rial to become conductive. When the critical concentration is reached, the conducting particles form a critical percolation cluster (also called infinite cluster), which has a fractal nature. Since percolation is a kind of geometric phase transition, it is scale-invariant.
Great attention has been paid to percolation problems in conducting-dielectric materials over the last decades. These problems have been intensively studied by Pike and Seager [3, 4], who discussed a large number of conductivity percolation problems and various methods of modelling of percolation systems, in particular the specificity of modelling particles and their distributions. The intensive experimental studies on electrical percolation in conductive mixtures of heterogeneous polymer solutions were performed by Wessling and Volk [5, 6] and Wessling [7], which describe a jumpwise character of changing the conductivity and confirm theoretical models used for modelling of such phenomena. Great attention has also been paid to metal-polymer conducting mixtures, where the metal powders were dispersed in the polymeric dielectric matrix. Roldughin and Vysotsky [8, 9] described the mechanisms of percolation in metal-filled polymer films, while Mamunya et al. [10] studied electrical and thermal conductivity in similar materials. With an increase of application of polymer composites and a development of new manufacturing technologies, attention has also been paid to polymer composites with carbon fibre and carbon nanotubes reinforcement. Several results of experimental studies on electrical percolation in these materials can be found e.g. in [11, 12].
The author’s work is concentrated on the continuum percolation systems of mixtures of conducting and dielectric polymers. For the investigation of this problem a numerical model was developed, which allows for the determination of critical percolation thresholds and accompanying clusters for various polymer mixtures for 2D and 3D problems [13]. Having the obtained results in the mentioned study, it was decided to analyse the obtained 2D critical percolation clusters in detail, which is the main goal of the present study. One of the important measures used for characterization of percolation clusters is the chemical distance which describes, in the case of electrical percolation, the shortest distance between adjacent conducting particles. Note that this distance varies from the Euclidean distance. Several studies on chemical distance in lattice-based percolation [14] and continuum percolation [15] have been reported. The presented definition of chemical distance distribution is the natural extension of the classical definition of chemical distance in a continuum percolation medium described in [15], which was inspired by similar formulation used in polymer chain-growth algorithm described in [14]. The chemical distance distribution is based on the shortest paths between domain boundaries (particles that belong to these paths equal 0), the values assigned to other particles outside the shortest paths determine the chemical distance from the shortest paths, and thus determine the possible paths of electric current in the percolation cluster. Additionally, the scaling self-similarity was studied based on evaluation of Minkowski-Bouligand dimension of the critical percolation clusters resulted from simulations, which, together with the values of Minkowski-Bouligand dimension, allows for examination of criticality and the fractal nature of considered clusters.
2. Percolation model
Since many polymers have no organized structure, the lattice-based percolation model is not suitable for modelling electrical percolation in such materials, therefore a continuum percolation model should be applied due to the random distribution of particles. The continuum percolation models can be classified into two groups according to the method of particles modelling: soft-core- and hard-core-based models. The soft-core models consist of the Swiss-cheese model, Boolean (or inversed Swiss-cheese) model and several other modifications. The general idea of these models is to generate points using the Poisson process of the constant concentration rate and place in these points voids (Swiss-cheese) or disks (Boolean) which, after reaching the percolation threshold by a considered system, constitute an infinite percolation cluster. Note that interpenetration of voids or disks is allowed in this class of models, therefore such models are suitable for flow modelling through the porous media [16] or wireless communication problems [17].
As opposite to soft-core models, in hard-core models the interpenetration between voids or disks is not allowed and such class of models is more realistic for modelling of electrical percolation and other percolation problems related to materials science. When the critical concentration of conducting particles is reached, the critical percolation cluster occurs and percolation occurs both in geometrical and conductivity domains. To date, several modifications of the hard-core model have been developed. The model which is more suitable for electrical percolation modelling was described in [18]. This model assumes that particles do not interpenetrate, but their conducting properties allow for tunnelling, i.e. the electron transferring between neighbouring particles in the dielectric medium. This model is called hard-core/soft-shell and was selected for modelling electrical percolation in the investigated mixture of conducting and dielectric polymers. This model is a hybrid between statistical and geometrical models, since conducting particles are distributed in a dielectric medium following Poisson distribution, whereas the conductivity analysis is performed based on geometrical properties of these particles with consideration of their dimensions and tunnelling properties. The tunnelling phenomenon occurs at the certain distance between two particles which is known as hopping distance. This phenomenon is observed in such compositions and described in several publications [19-21]. In order to model various scenarios of electrical percolation, three conducting polymers were selected: polypyrrole (PPy), polythiophene (PTh) and polyaniline (PANI). The physical properties of the considered conducting polymers are presented in Table 1 based on experimental results of their determination. The dielectric matrix was assumed as epoxy with a conductivity of σ2 = 7.9×10–16 S/cm [22]. Assuming that the tunnelling effect occurs with a probability tending to unity, the conductivity on the hopping distance R1 around the particle is the same as for the conducting polymer.
Table 1
Physical properties of the considered conducting polymers
|
Polymer |
Particle size r0 [nm] |
Hopping distance r1 [nm] |
Maximum conductivity s1 [S/cm] |
|
PPy |
35 [23] |
181 [26] |
1000 [28] |
|
PTh |
1000 [24] |
5 [24] |
190 [28] |
|
PANI |
50 [25] |
2.04 [27] |
60 [28] |
The conductivity decreases rapidly on the interphase of R1 and a dielectric matrix, however, one can assume some distance R2, at which the conductivity decreases from the value of conducting polymer σ1 to the conductivity value of dielectric σ2. This leads to the formulation of a two-layer model of a soft-shell around the particle, as similarly presented in [11]. The decrease of conductivity in this region is described by the following law:
| (1) |
The logarithmic character of
conductivity decrease is assumed as an inverse of the exponential temperature-conductivity models
presented by Subramaniam et al. [29]. Because the conductivity decreases
according to (1) and thus ![]() it is suitable to define the critical value, below which it can be
assumed that there is no conductivity in a polymer mixture. It was assumed that
this critical value is equal to the conductivity of deionized water: σc = 5.5×10–8 S/cm,
which is usually assumed as a limit value of
conductivity [30, 31]. Based on (1) and considering the values pre-
sented in Table 1 and assumed limit value of
conductivity, it is possible to determine numerical
values of critical radii Rc of the second layer of soft-shell
at which the conductivity is possible: Rc,PPy =
468.2 nm, Rc,PTh = 2011 nm, Rc,PANI =
104.48 nm.
it is suitable to define the critical value, below which it can be
assumed that there is no conductivity in a polymer mixture. It was assumed that
this critical value is equal to the conductivity of deionized water: σc = 5.5×10–8 S/cm,
which is usually assumed as a limit value of
conductivity [30, 31]. Based on (1) and considering the values pre-
sented in Table 1 and assumed limit value of
conductivity, it is possible to determine numerical
values of critical radii Rc of the second layer of soft-shell
at which the conductivity is possible: Rc,PPy =
468.2 nm, Rc,PTh = 2011 nm, Rc,PANI =
104.48 nm.
In the constructed model, conducting particles were modelled as a dispersion in the epoxy matrix following Poisson distribution process. Considering that the domain should be sufficiently large with respect to dimensions of a single conducting particle, the following dimensions of domains were assumed: for PPy/epoxy mixture - 0.04×0.04 mm2, for PTh/epoxy mixture - 0.1×0.1 mm2 and for PANI/epoxy mixture - 0.01×0.01 mm2. The algorithm of search of critical concentration of conducting particles in a dielectric medium was implemented in Matlab® and the resulting percolation clusters were obtained [13]. The properties of obtained percolation clusters are presented in Table 2. These clusters were then analysed in order to determine the chemical distance distribution as well as their self-similarity and fractal dimension.
Table 2
Properties of critical percolation clusters
|
Mixture |
No. of conducting particles, ncp |
No. of particles in critical percolation cluster, ncpc |
Percolation threshold, η |
|
PPy/epoxy |
7901 |
6452 |
0.01900 |
|
PTh/epoxy |
2579 |
1839 |
0.81022 |
|
PANI/epoxy |
9504 |
5543 |
0.74644 |
3. Characterization of critical percolation clusters
In order to investigate the electrical properties of resulting percolation models of conducting/dielectric polymers at the critical concentrations of conducting particles, it is essential to evaluate possible conductivity paths of current. In percolation problems, it can be characterized by determination of chemical distance, which is a measure that describes the shortest paths between certain conducting particles. In this study, the extension of this measure is proposed, which allows for evaluation of all possible paths of current with corresponding distances in the entire percolation cluster.
Additionally, the self-similarity of the resulting percolation clusters was examined based on determination of Minkowski-Bouligand dimension, which is often used for quantitative characterization of percolation clusters [8, 9, 32, 33].
3.1. Chemical distance distribution
The chemical distance distribution was determined as follows. Firstly, the particles located the closest to the boundaries of a given domain were found, and the classic chemical distance algorithm was applied in order to determine all shortest paths between these particles. In order to determine the shortest paths, an adjacency matrix for all particles that belong to the critical percolation cluster was constructed. The shortest path is determined for every pair of defined particles that represent particular boundaries of a domain. For the determined paths the values of chemical distance distribution are assumed to be equal to zero. Then, for each particle that does not belong to the determined shortest paths, the chemical distance is determined. The algorithm considers the shortest distance to a given particle, i.e. if the distance between the particle p (that does not belong to the shortest paths) and the particle s2 (that belongs to the shortest paths) is lower than the distance between the particle p and particle s1 the lower value substitutes the higher one. While the distance between a given particle and the shortest paths grows, the distances between intermediate particles are added up.
The obtained chemical distance distributions for the critical percolation clusters of considered mixtures of conducting/dielectric polymers are presented in Figures 1-3.
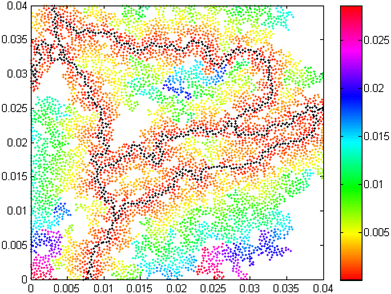
Fig. 1. Chemical distance distribution of the critical percolation cluster of PPy/epoxy mixture
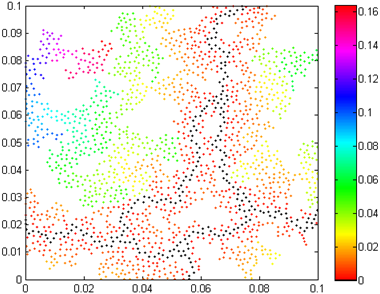
Fig. 2. Chemical distance distribution of the critical percolation cluster of PTh/epoxy mixture
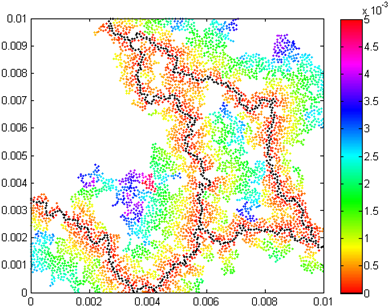
Fig. 3. Chemical distance distribution of the critical percolation cluster of PANI/epoxy mixture
In the presented chemical distance distributions the shortest paths are marked in black.
Besides the fact that chemical distance distribution can be considered as a measure for characterization and distinguishability of percolation clusters in a mathematical sense (see [34] for instance), it can be useful for prediction of thermo-electro-mechanical behaviour of materials made of discussed mixtures of polymers and other multi-component mixtures.
3.2. Self-similarity of critical percolation clusters
In order to prove that the obtained
percolation clusters are critical, and thus, have a fractal nature, the
Minkowski-Bouligand dimension ![]() was determined
for them following the next scaling law:
was determined
for them following the next scaling law:
| (2) |
where C is a considered cluster and N(ε)
is a number of square boxes of side length ε required to cover the
entire cluster. The calculations are performed iteratively by changing ε
and counting N(ε). The selection of Minkowski-Bouligand
dimension from a variety of formulations of fractal dimension was performed due
to its fundamentality and simplicity of application. Moreover, in the presented
study,
the selected formulation does not influence
the resulted values. The resulting values are plotted in the log-log
plot of N(ε) versus 1/ε and then its linear
regression is
determined. The slope of a regression
line gives ![]() value, while the accuracy of fitting of estimated values on the log-log plot to the regression
line determines
a degree of self-similarity of the considered percolation cluster.
value, while the accuracy of fitting of estimated values on the log-log plot to the regression
line determines
a degree of self-similarity of the considered percolation cluster.
The ![]() was determined for each
considered percolation cluster following the
above-described procedure and presented in Figure 4. In order to obtain a
better fit,
was determined for each
considered percolation cluster following the
above-described procedure and presented in Figure 4. In order to obtain a
better fit, ![]() was determined for the range of ε
from 24 to 27 with a step of 20.1.
was determined for the range of ε
from 24 to 27 with a step of 20.1.
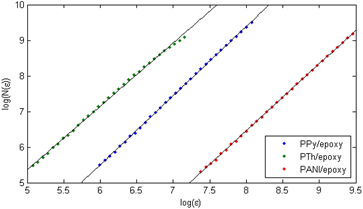
Fig. 4. The slopes for the investigated percolation clusters of various mixtures of conducting/dielectric polymers
As observed, the regression lines fit well to
the determined values during calcu-
lation of ![]() which proves the fractal nature
of the analysed percolation clus-
ters and additionally shows that they are critical for
particular electrical percolation problems defined previously. The fractal
dimensions obtained for these clusters
are as follows: for PPy/epoxy mixture - 1.9417, for PTh/epoxy - 1.782 and for
PANI/epoxy - 1.8811. In contrast to lattice-based percolation clusters, which
are characterized by constant values
of
which proves the fractal nature
of the analysed percolation clus-
ters and additionally shows that they are critical for
particular electrical percolation problems defined previously. The fractal
dimensions obtained for these clusters
are as follows: for PPy/epoxy mixture - 1.9417, for PTh/epoxy - 1.782 and for
PANI/epoxy - 1.8811. In contrast to lattice-based percolation clusters, which
are characterized by constant values
of ![]() for various configurations of lattices (see [35]), in the case
of continuum percolation the values of
for various configurations of lattices (see [35]), in the case
of continuum percolation the values of ![]() vary and
depend on numerous factors (see e.g. [36, 37]). The obtained values of
vary and
depend on numerous factors (see e.g. [36, 37]). The obtained values of ![]() for the considered percolation clusters are in agreement with the values
obtained for similar problems (see e.g. [37-39]).
for the considered percolation clusters are in agreement with the values
obtained for similar problems (see e.g. [37-39]).
4. Conclusions
The presented study discusses the quantitative characterization of critical percolation clusters obtained from numerical simulation of mixtures of various conducting polymers with a dielectric one. The chemical distance distribution measure is introduced in this paper and applied for mapping of all possible conductivity paths in the considered percolation clusters with evaluation of a chemical distance of each particle that belongs to the percolation cluster to the shortest paths of electrical conductivity. The self-similarity of the analysed clusters was examined based on their scaling properties obtained using the formulation of Minkowski-Bouligand dimension. The obtained results confirmed that the considered clusters have a fractal nature and the obtained values of the Minkowski-Bouligand dimension correspond to typical values of percolation clusters occurred in a two-dimensional domain.
Acknowledgements
The publication is financed from the funds granted by the Foundation for Polish Science according the contract no. 128/UD/SKILLS/2015 on realization of award granted in the INTER contest, realized within the framework of the SKILLS programme, cofinanced from the European Social Fund. A possibility of carrying out computations on the supercomputer IBM Blade-Center HS21 in the Academic Computer Centre CYFRONET AGH under the computational Grant No. MNiSW/IBM_BC_HS21/PŚląska/012/2013 is gratefully acknowledged.
References
[1] Flory P.J., Molecular size distribution in three dimensional polymers, J. Am. Chem. Soc. 1941, 63(11), 3083-3090.
[2] Stockmayer W.H., Theory of molecular size distribution and gel formation in branched-chain polymers, J. Chem. Phys. 1943, 11(2), 45-55.
[3] Pike G.E., Seager C.H., Percolation and conductivity. A computer study. I, Phys. Rev. B 1974, 10(4), 1421-1434.
[4] Pike G.E., Seager C.H., Percolation and conductivity. A computer study. II, Phys. Rev. B 1974, 10(4), 1435-1446.
[5] Wessling B., Volk H., Post-polymerization processing of conductive polymers: a way of converting conductive polymers to conductive materials? Synthetic Met. 1986, 15, 183-193.
[6] Wessling B., Volk H., Thermoplastic conversion of ‘doped’ polyaniline from the amorphous to a partially crystal state, Synthetic Met. 1986, 16, 127-131.
[7] Wessling B., Electrical conductivity in heterogeneous polymer systems, [in:] Electronic Properties of Conjugated Polymers, eds. H. Kuzmany, M. Mehring, S. Roth, Springer Ser. Solid State Sci., Springer, New York 1987, 76, 407-412.
[8] Vysotsky V.V., Roldughin V.I., Aggregate structure and percolation properties of metal-filled polymer films, Colloid Surf. A 1999, 160(2), 171-180.
[9] Roldughin V.I., Vysotsky V.V., Percolation properties of metal-filled polymer films, structure and mechanisms of conductivity, Prog. Org. Coat. 2000, 39, 81-100.
[10] Mamunya Y.P., Davydenko V.V., Passis P., Lebedev E.V., Electrical and thermal conductivity of polymers filled with metal powders, Eur. Polym. J. 2002, 38(9), 1887-1897.
[11] Qiao R., Brinson L.C., Simulation of interphase percolation and gradients in polymer nanocomposites, Compos. Sci. Technol. 2009, 69, 491-499.
[12] Bauhofer W., Kovacs J.Z., A review and analysis of electrical percolation in carbon nanotube polymer composites, Compos. Sci. Technol. 2009, 69, 1486-1498.
[13] Katunin A., Krukiewicz K., Electrical percolation in composites of conducting polymers and dielectrics, J. Polym. Eng. 2015, 35(8), 731-741.
[14] Brereton T., Hirsch C., Schmidt V., Kroesse D., A critical exponent for shortest-path scaling in continuum percolation, J. Phys. A: Math. Theor. 2014, 47(50), 505003.
[15] Blavatska V., Fricke N., Janke W., Polymers in disordered environments, Condens. Matter Phys. 2014, 17(3), 1-11.
[16] Hunt A., Percolation Theory for Flow in Porous Media, Springer, New York 2005.
[17] Franceschetti M., Meester R., Random Networks for Communication: From Statistical Physics to Information Networks, Cambridge University Press, New York 2007.
[18] Belashi A., Percolation Modeling in Polymer Nanocomposites, PhD thesis, University of Toledo, Toledo 2011.
[19] Pelster R., Nimtz G., Wessling B., Mesoscale change transport in polyaniline, J. Phys. II France 1994, 4, 549-553.
[20] Pelster R., Nimtz G., Wessling B., Fully protonated polyaniline: Hopping transport on a mesoscopic scale, Phys. Rev. B 1994, 49, 12718-12723.
[21] Angappane S., Srinivasan D., Rangarajan G., Prasad V., Subramanyam S.V., Wessling B., Transport and magneto-transport study on some conducting polyanilines, Physica B 2000, 284-288, 1982-1983.
[22] Barrau S., Demont P., Perez E., Peigney A., Laurent C., Lacabanne C., Effect of palmitic acid on the electrical conductivity of carbon nanotubes-epoxy resin composites, Macromolecules 2003, 36, 9678-9680.
[23] Ángeles Corres M., Mugica A., Carrasco P.M., Cortazár M.M., Effect of crystallization on morphology-conductivity relationship in polypyrrole/(ε-caprolactone) blends, Polymer 2006, 47(19), 6759-6764.
[24] Reedijk J.A., Martens H.C.F., Brom H.B., Dopant-induced crossover from 1D to 3D charge transport in conjugated polymers, Phys. Rev. Lett. 1999, 83, 3904-3907.
[25] Bhadra J., Sarkar D., Size variation of polyaniline nanoparticles dispersed in polyvinyl alcohol matrix, Bull. Mater. Sci. 2010, 33(5), 519-523.
[26] Basavaraja C., Kim N.R., Jo E.A., Pierson R., Huh D.S., Venkataraman A., Transport properties of polypyrrole films doped with sulphonic acids, Bull. Korean Chem. Soc. 2009, 30, 2701-2706.
[27] Kondawar S.B., Deshpande M.D., Agrawal S.P., Transport properties of conductive polyaniline nanocomposites based on carbon nanotubes, Int. J. Compos. Mater. 2012, 2(3), 32-36.
[28] Craver C.D., Carraher C.E., Applied Polymer Science: 21st Century, Elsevier Science, Oxford 2000.
[29] Subramaniam C.K., Kaiser A.B., Gilberd P.W., Liu C.-J., Wessling B., Conductivity and thermopower of blends of polyaniline with insulating polymers (PETG and PMMA), Solid State Commun. 1996, 97(3), 235-238.
[30] Aylward G., Findlay T., SI Chemical Data, Wiley, New York 1994.
[31] Yu P.Y., Cardona M., Fundamentals of Semiconductors: Physics and Material Properties, Springer-Verlag, Berlin 2010.
[32] Voss R.F., The fractal dimension of percolation cluster hulls, J. Phys. A 1984, 17, L373-L377.
[33] Lukashevich V.N., Lukashevich O.D., Kharii R.I., A model of fractals for cement-based fiber-reinforced pavement base course, Vestnik TSUAB 2013, 1, 178-188.
[34] Strelniker Y.M., Havlin S., Bunde A., Fractals and percolation, [in:] Encyclopedia of Complexity and Systems Science, ed. R.A. Meyers, Springer-Verlag, New York 2009, 3847-3858.
[35] Tarasevich Y.Y., Percolation: Theory, Applications, Algorithms, Editoria URSS Press, Moscow 2002 (in Russian).
[36] Isichenko M.B., Percolation, statistical topography, and transport in random media, Rev. Mod. Phys. 1992, 64(4), 961-1043.
[37] Havlin S., Ben-Avraham D., Diffusion in disordered media, Adv. Phys. 2002, 51(1), 187-292.
[38] Nakamura M., Fractal property of two-dimensional continuum percolation clusters, Phys. Rev. A 1986, 34(4), 3356-3361.
[39] He D., Ekere N.N., Cai L., Two-dimensional percolation and cluster structure of the random packing of binary disks, Phys. Rev. E 2002, 65, 061304.

