1D generalized dual-phase lag equation. Sensitivity analysis with respect to the porosity
Grażyna Kałuża
,Ewa Majchrzak
,Łukasz Turchan
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
1D GENERALIZED DUAL-PHASE LAG EQUATION SENSITIVITY ANALYSIS WITH RESPECT TO THE POROSITY
Grażyna Kałuża, Ewa Majchrzak, Łukasz Turchan
Institute of Computational Mechanics and Engineering
Silesian University of Technology
Gliwice, Poland
grazyna.kaluza@polsl.pl, ewa.majchrzak@polsl.pl, lukasz.turchan@polsl.pl
Abstract. Thermal processes occurring in the heated tissue are described by the 1D gener- alized dual-phase lag equation supplemented by appropriate boundary and initial conditions. Using the sensitivity analysis method, the additional problem connected with the porosity is formulated. Both problems are solved by means of the explicit scheme of the finite difference method. In this way it is possible to estimate the temperature changes due to the perturbation of porosity. In the final part of the paper, the example of computation is shown and the conclusions are formulated.
Keywords: bioheat transfer, generalized dual-phase lag model, sensitivity analysis, finite difference method
1. Introduction
Thermal phenomena occurring in heated tissue are described using the various mathematical models, e.g. [1-8]. One of them is the dual-phase lag equation [9-11] in which two time parameters τq and τT appear. The parameter τq is the phase lag of the heat flux and parameter τT is the phase lag of the temperature gradient. Extension of this model is the generalized dual-phase lag equation [12-15]. In this equation the phase lag times τq and τT are expressed in terms of the blood and tissue properties, the interphase convective heat transfer coefficient and the blood perfusion rate. Generalized dual-phase lag equation contains additional parameters, it means the coupling factor G, the porosity ε defined as a ratio of blood volume to total volume and the blood temperature Tb.
In this paper the 1D generalized dual-phase lag equation (GDPLE) under the assumption that the blood temperature is constant is considered. The aim of investigations is to estimate the changes of the temperature field due to the perturbations of porosity ε. For this purpose, the direct method of sensitivity analysis is applied [16-20]. In this case the mathematical model consists of the basic problem (GDPLE supplemented by appropriate boundary and initial conditions) and the additional problem resulting from the differentiation of governing equations. These problems are solved using the explicit scheme of the finite difference method for hyperbolic equations [14, 15]. In the final part of the paper the example of computations and conclusions are presented.
2. Formulation of the problem
The generalized dual-phase lag equation describing the heat transfer processes occurring in the heated tissues is based on the theory of porous media [6, 12, 13]. In this approach the tissue is divided into two regions: the vascular region (blood vessels) and the extravascular region (tissue). An important parameter in this model is the porosity ε, it means the ratio of blood volume to total volume. Using this parameter, the effective thermal conductivity
| (1) |
and effective heat capacity
| (2) |
are defined, where λ, λb are the thermal conductivities of tissue and blood, respectively, ρ, ρb are the densities, c, cb are the specific heats.
Under the assumption that the metabolic heat sources Q, Qb and the blood temperature Tb are constant, the generalized dual-phase lag equation for 1D problem takes the form [13, 15, 16]
| (3) |
where T = T(x, t) is the temperature, x is the spatial co-ordinate, t is the time, G is the coupling factor, τq and τT are the phase lags for heat flux and temperature gradient. The equation (3) is supplemented by boundary conditions [10, 11]
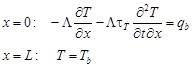 | (4) |
and the initial ones
| (5) |
where qb is the known constant boundary heat flux, Tb is the boundary temperature and Tp is the initial temperature of biological tissue.
The coupling factor G and the phase lags τq, τT are defined as [12, 14]
| (6) |
| (7) |
| (8) |
where A is the the volumetric heat transfer area between tissue and blood, α is the heat transfer coefficient and w is the blood perfusion rate.
The volumetric heat transfer area between tissue and blood can be determined from the dependence A = k Pb/V, where k is the number of blood vessels located in the volume V and Pb is the surface area between the single vessel and tissue. As mentioned before, the porosity ε is the ratio of blood volume to total volume: ε = kVb/V and it follows that A = ε Pb/Vb . The heat transfer coefficient can be calculated from the Nusselt number Nu = α d/λb, where d is the vessel diameter. Assuming that the diameter of all blood vessels is the same, then Pb/Vb and α are constants.
3. Sensitivity analysis
To estimate the temperature changes due to the changes of porosity, the direct method of sensitivity analysis can be applied [16-20].
The equation (3) is differentiated with respect to the porosity ε and then
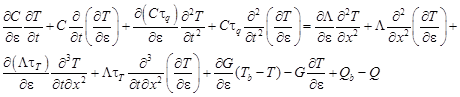 | (9) |
or
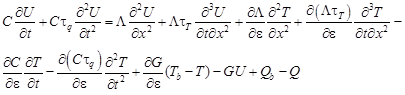 | (10) |
where U = ∂T/∂ε is the sensitivity function.
The boundary conditions (4) and the initial conditions (5) are also differentiated with respect to ε. Thus
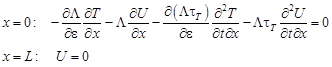 | (11) |
and
| (12) |
In equation (10) the derivatives of thermal parameters are determined as follows
| (13) |
| (14) |
| (15) |
The equations (10)-(12) create the additional problem which is coupled with the basic problem (equations (3)-(5)).
4. Method of solution
To solve both the basic problem and the additional one, the finite difference method in the version presented in [21] is applied. The geometrical mesh with constant step h and time step ∆t are introduced.
For the internal node i the following approximate form of equation (3) is proposed
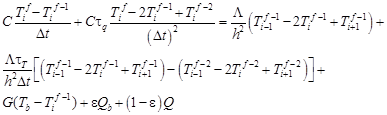 | (16) |
After mathematical manipulations one obtains (i = 1, 2, …, n − 1)
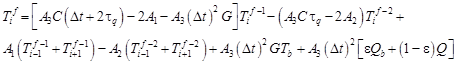 | (17) |
where
| (18) |
For the boundary node i = 0 one has
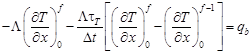 | (19) |
and next
| (20) |
From equation (20) it follows that
| (21) |
In the similar way the equation (10) connected with the sensitivity function is approximated
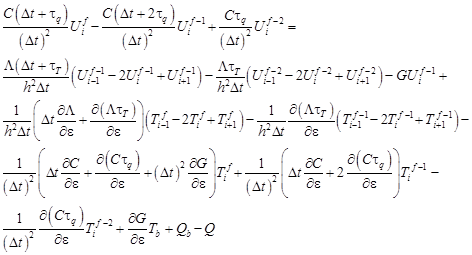 | (22) |
From the equation (22) it results that (i = 1, 2, …, n − 1)
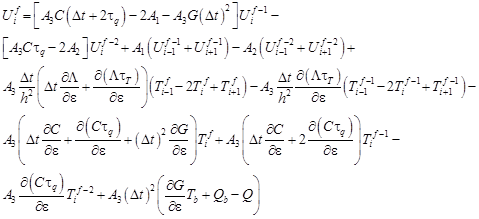 | (23) |
For the boundary node i = 0 one obtains (cf. equation (11))
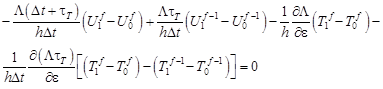 | (24) |
hence
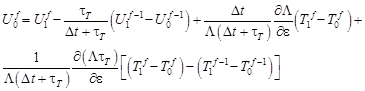 | (25) |
Because the explicit scheme of the finite difference method is applied, the stability criteria should be fulfilled [21]
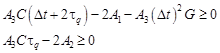 | (26) |
5. Results of computations
The layer of biological tissue of thickness L = 0.01 m is considered. On the surface x = 0 the Neumann condition qb = 1500 W/m2 is assumed and on the surface x = L the Dirichlet condition Tb = 37°C is accepted. The initial temperature of tissue is equal to Tp = 37°C. The thermophysical parameters of tissue and blood are collected in Table 1. The blood perfusion rate w = 5 kg/(m3s), the porosity ε = 0.1637, the vessels diameter d = 0.00456 m, the Nusselt number Nu = 4.93.
The calculations were made using the explicit scheme of the finite difference method assuming the grid step h = 0.0002 m and time step ∆t = 0.01 s.
Table 1
Thermophysical parameters
|
Parameter |
Tissue |
Blood |
|
Thermal conductivity [W/(m∙K)] |
0.3 |
0.5 |
|
Density [kg/m3] |
1000 |
1060 |
|
Specific heat [J/(kg∙K)] |
4000 |
3770 |
|
Metabolic heat source [W/m3] |
240 |
250 |
In Figure 1 the distribution of sensitivity function after 60, 120 and 180 seconds is presented. Figures 2 and 3 illustrate the courses of temperature and sensitivity function at the points x = 0 (heated surface), x = 1 mm, x = 2 mm, x = 3 mm and x = 4 mm. As might be expected, the biggest changes of the sensitivity function occur near the heated surface (Fig. 1).
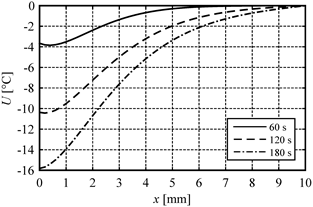
Fig. 1. Distribution of the sensitivity function after 60, 120 and 180 seconds
Knowledge of the sensitivity function allows one, among others, to estimate the changes of temperature due to the perturbation of the parameter considered: ∆T = U∆ε, where ∆ε is the assumed perturbation of the porosity (e.g. ∆ε = 0.05ε). In Table 2 the changes of temperature for different values of ∆ε at the point x = 0 are collected. As can be seen, changes in temperature increase both with an increase of ∆ε as well as with the duration of the heating process.
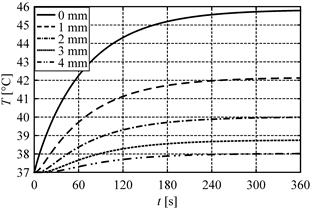
Fig. 2. Heating curves at selected points
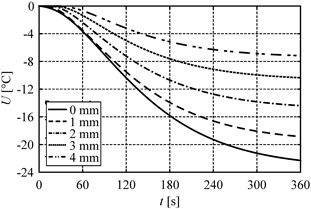
Fig. 3. Course of sensitivity function at selected points
Table 2
Change of temperature due to the perturbation of porosity (x = 0)
|
Time [s] |
∆T [°C] |
||
|
∆ε = 0.01ε |
∆ε = 0.05ε |
∆ε = 0.1ε |
|
|
60 |
–0.01 |
–0.03 |
–0.06 |
|
120 |
–0.02 |
–0.09 |
–0.17 |
|
180 |
–0.03 |
–0.13 |
–0.26 |
|
240 |
–0.03 |
–0.16 |
–0.32 |
|
300 |
–0.03 |
–0.17 |
–0.35 |
|
360 |
–0.04 |
–0.18 |
–0.37 |
6. Conclusions
The 1D generalized dual-phase lag equation describing the thermal processes occurring in the heated biological tissue is considered. The sensitivity analysis with respect to the porosity is presented. Here, the diameter of vessels is assumed as a constant and then the porosity contains information only about the density of blood vessels.
As might be expected, the highest temperature perturbation occurs near the heated boundary, which can be seen in Figure 1. On the other hand, however, the heating time also has a meaningful impact on the results (cf. Fig. 3). It should be noted that in each case, the sensitivity function takes the negative values. This results from an increase in porosity, which entails in decreasing the tissue temperature, of course. As can be seen in Table 2, the porosity perturbation of 1% causes very small changes in temperature (< 0.1%), while the porosity perturbation of 5 or 10% noticeably changes the values of temperature.
The presented approach can be extended for 3D problems and two-temperature models [12, 14, 22] in which the blood temperature is determined from the additional equation coupled with the generalized dual-phase lag equation.
Acknowledgement
This work is supported by the project BK-255/RMT4/2016.
References
[1] Torvi D.A., Dale J.D., A finite element model of skin subjected to a flash fire, Journal of Bio- mechanical Engineering 1994, 116, 250-255.
[2] Jamil M., Ng E.Y.K., Ranking of parameters in bioheat transfer using Taguchi analysis, Inter- national Journal of Thermal Sciences 2013, 63, 15-21.
[3] Mochnacki B., Piasecka-Belkhayat A., Numerical modeling of skin tissue heating using the interval finite difference method, MCB: Molecular & Cellular Biomechanics 2013, 10, 3, 233-244.
[4] Majchrzak E., Mochnacki B., Dziewoński M., Jasiński M., Numerical modelling of hyperthermia and hypothermia processes, Advanced Materials Research 2011, 268-270, 257-262.
[5] Duda M., Mochnacki B., 3D model of thermal interactions between human forearm and environment, Journal of Applied Mathematics and Computational Mechanics 2015, 14, 4, 17-23.
[6] Khaled A.R.A., Vafai K., The role of porous media in modeling of flow and heat transfer in biological tissues, International Journal of Heat and Mass Transfer 2003, 46, 4989-5003.
[7] Ciesielski M., Mochnacki B., Application of the control volume method using the Voronoi polygons for numerical modeling of bio-heat transfer processes, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 927-935.
[8] Jasiński M., Modelling of tissue thermal injury formation process with application of direct sensitivity method, Journal of Theoretical and Applied Mechanics 2014, 52, 4, 947-957.
[9] Zhou J., Chen J.K., Zhang Y., Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation, Computers in Biology and Medicine 2009, 39, 286-293.
[10] Majchrzak E., Numerical solution of dual phase lag model of bioheat transfer using the general boundary element method, CMES: Computer Modeling in Engineering & Sciences 2010, 69, 1, 43-60.
[11] Majchrzak E., Turchan Ł., The general boundary element method for 3D dual-phase lag model of bioheat transfer, Engineering Analysis with Boundary Elements 2015, 50, 76-82.
[12] Zhang Y., Generalized dual-phase lag bioheat equations based on nonequilibrium heat transfer in living biological tissues, International Journal of Heat and Mass Transfer 2009, 52, 4829-4834.
[13] Nakayama A., Kuwahara F., A general bioheat transfer model based on the theory of porous media, International Journal of Heat and Mass Transfer 2008, 51, 3190-3199.
[14] Majchrzak E., Turchan Ł., Numerical analysis of tissue heating using the generalized dual phase lag model, [in:] Recent Advances in Computational Mechanics, eds. T. Łodygowski, J. Rakowski & P. Litewka, CRC Press, London 2014, 355-362.
[15] Jasiński M., Majchrzak E., Turchan Ł., Numerical analysis of the interactions between laser and soft tissues using dual-phase lag model, Applied Mathematical Modeling 2016, 40, 2, 750-762.
[16] Kleiber M., Parameter Sensitivity, J. Wiley & Sons Ltd., Chichester 1997.
[17] Dziewoński M., Mochnacki B., Szopa R., Sensitivity of biological tissue freezing process on the changes of cryoprobe cooling rate, Proceedings of 16th International Conference, Mechanika, Kaunas University of Technology, 2011, 82-87.
[18] Majchrzak E., Mochnacki B., Sensitivity analysis of transient temperature field in microdomains with respect to the dual phase lag model parameters, International Journal for Multiscale Computational Engineering 2014, 12, 1, 65-77.
[19] Mochnacki B., Majchrzak E., Identification of macro and micro parameters in solidification model, Bulletin of the Polish Academy of Sciences, Technical Sciences 2007, 55, 1, 107-113.
[20] Mochnacki B., Majchrzak E., Sensitivity of the skin tissue on the activity of external heat sources, CMES: Computer Modeling in Engineering and Sciences 2003, 4, 3-4, 431-438.
[21] Majchrzak E., Kałuża G., Heat flux formulation for 1D dual-phase lag equation, Journal of Applied Mathematics and Computational Mechanics 2015, 14, 1, 71-78.
[22] Majchrzak E., Turchan Ł., Dziatkiewicz J., Modeling of skin tissue heating using the generalized dual-phase lag equation, Archives of Mechanics 2015, 67, 6, 417-437.

