The potentials method for the M/G/1/m queue with customer dropping and hysteretic strategy of the service time change
Yuriy Zhernovyi
,Bohdan Kopytko
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE POTENTIALS METHOD FOR THE M/G/1/M QUEUE WITH CUSTOMER DROPPING AND HYSTERETIC STRATEGY OF THE SERVICE TIME CHANGE
Yuriy Zhernovyi 1, Bohdan Kopytko 2
1 Ivan
Franko National University of Lviv
Lviv, Ukraine
2 Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
yu.zhernovyi@lnu.edu.ua, bohdan.kopytko@im.pcz.pl
Abstract. We
propose a method for determining the probabilistic characteristics of the ![]() queueing system with the random dropping of arrivals and
distribution of the service time depending on the queue length. Two sets of
service modes, with the service time distribution functions
queueing system with the random dropping of arrivals and
distribution of the service time depending on the queue length. Two sets of
service modes, with the service time distribution functions ![]() and
and ![]() respectively,
are used according to the two-threshold hysteretic strategy. The Laplace
transforms for the distribution of the number
of customers in the system during the busy period and for the distribution
function of the length of the busy period are found. The developed algorithm
for calculating the stationary characteristics of the system is tested with the
help of a simulation model constructed
with the assistance of GPSS World tools.
respectively,
are used according to the two-threshold hysteretic strategy. The Laplace
transforms for the distribution of the number
of customers in the system during the busy period and for the distribution
function of the length of the busy period are found. The developed algorithm
for calculating the stationary characteristics of the system is tested with the
help of a simulation model constructed
with the assistance of GPSS World tools.
Keywords: single-channel queueing system, random dropping of customers, hysteretic strategy for service time, potentials method, stationary characteristics
1. Introduction
Studies show [1-3] that the random dropping of arrivals is a powerful tool for parameter control of a queueing system. The dropping can not only regulate the queue length, loss probability of customers, waiting time, and queue length variance, but also regulate several of these parameters simultaneously.
In order to increase the system capacity, threshold strategies of the service intensity (service time) change are used in queueing systems. In the general case, the essence of this strategy is that the service time distribution depends on the number of customers in the system at the beginning of each customer service [4]. With the help of the potentials method, we have developed an efficient algorithm for computing the stationary distribution of the number of customers in the systems with threshold functioning strategies [4-8].
In this paper we consider the ![]() queueing system with random dropping of
customers and distribution of the service time depending on the queue length.
Two sets of service modes (the main mode and overload mode), with the service
time distribution functions
queueing system with random dropping of
customers and distribution of the service time depending on the queue length.
Two sets of service modes (the main mode and overload mode), with the service
time distribution functions ![]() and
and ![]() respectively, are used according to the
two-threshold hysteretic strategy. The overload mode with the functions
respectively, are used according to the
two-threshold hysteretic strategy. The overload mode with the functions ![]() starts functioning if at the beginning
of service of a customer, the number of customers in the system satisfies the
condition
starts functioning if at the beginning
of service of a customer, the number of customers in the system satisfies the
condition ![]() The return to the main mode with the
functions
The return to the main mode with the
functions ![]() carried out at the beginning of service
of the customer, for which
carried out at the beginning of service
of the customer, for which ![]() where
where ![]()
Each arriving customer can be accepted for
service with a probability depending on the queue length. We assign this
probability according to the rule: if at the time of the arrival of a customer ![]() customers are in the system, then the
customer is
accepted for service with probability
customers are in the system, then the
customer is
accepted for service with probability ![]() and
leaves the system (is discarded) with probability
and
leaves the system (is discarded) with probability ![]() Fix a threshold value
Fix a threshold value ![]()
![]() and suppose that
and suppose that ![]() for
for ![]() and
and![]() for
for ![]() In
paper [9] we also studied
the queueing systems with random dropping of arrivals. In contrast to this
article, in [9] the probability
In
paper [9] we also studied
the queueing systems with random dropping of arrivals. In contrast to this
article, in [9] the probability ![]() does not change
during the time interval from the beginning to the completion of service of
each customer.
does not change
during the time interval from the beginning to the completion of service of
each customer.
2. Basic random walks
We consider the ![]() system, where
system, where ![]() is the maximum number of
custom-
ers in the queue. Let
is the maximum number of
custom-
ers in the queue. Let ![]() be a parameter of the
exponential distribution of the time intervals between moments of arrival of
customers. Suppose that, if at the beginning of service of a customer the
number of customers in the system is equal to
be a parameter of the
exponential distribution of the time intervals between moments of arrival of
customers. Suppose that, if at the beginning of service of a customer the
number of customers in the system is equal to ![]() then the service time of this
customer is a random variable with distribution function
then the service time of this
customer is a random variable with distribution function ![]() for the main mode and
for the main mode and ![]()
![]() for the overload mode.
for the overload mode.
Denote by ![]() the
conditional probability, provided that at the initial time the number of
customers in the queueing system is equal to
the
conditional probability, provided that at the initial time the number of
customers in the queueing system is equal to ![]() and
by
and
by ![]() (P) the conditional expectation
(the conditional probability) if the system starts to work at the time of
arrival of the first customer. Let
(P) the conditional expectation
(the conditional probability) if the system starts to work at the time of
arrival of the first customer. Let ![]() be the number
of customers arriving in the system during the time interval
be the number
of customers arriving in the system during the time interval ![]() Let
Let
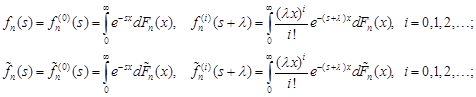 |
For ![]() and
and ![]() consider the sequences
consider the sequences ![]()
![]() and
and
![]() defined by the relations:
defined by the relations:
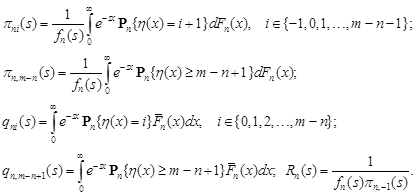 | (1) |
Similarly, for ![]() and
and ![]() we set the sequences
we set the sequences ![]()
![]() and
and ![]()
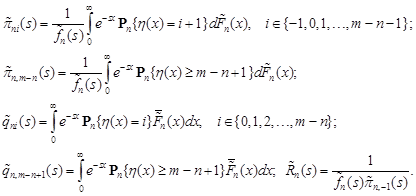 | (2) |
Let ![]() and
and ![]() denote the exponentially distributed
random variables with parame-
ter
denote the exponentially distributed
random variables with parame-
ter ![]() and
and ![]() respectively, and
respectively, and ![]() is a random variable distributed
according to the law of Pascal, that is,
is a random variable distributed
according to the law of Pascal, that is, ![]()
![]() It is known [10], that
It is known [10], that ![]() that is, as a result of a random
decimation of the simplest flow we
obtain a simplest flow.
that is, as a result of a random
decimation of the simplest flow we
obtain a simplest flow.
Given the above, for ![]() we
find
we
find
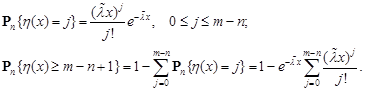 |
For ![]() we obtain
we obtain
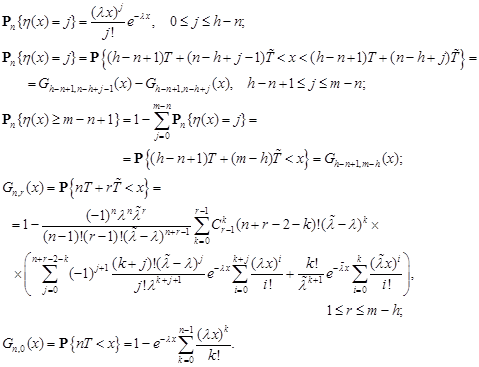 |
Taking into account the expressions for ![]() and equalities
and equalities
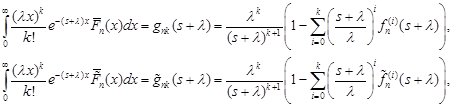 |
by (1), (2) calculate the terms of the sequences
![]()
![]() and
and ![]()
For ![]() we find
we find
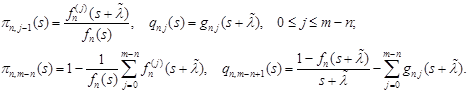 | (3) |
For ![]() and
and ![]() we obtain
we obtain
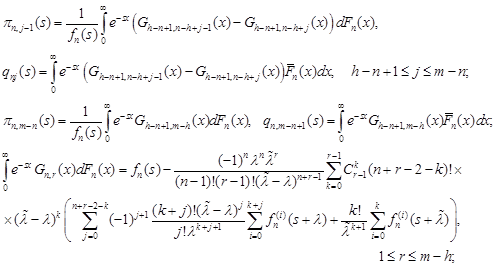 |
| (4) |
Expressions for ![]() and
and ![]() are similar with presented in (3) and
(4) for
are similar with presented in (3) and
(4) for ![]() or
or ![]() and
for
and
for ![]() respectively, if we
replace
respectively, if we
replace ![]() and
and ![]() by
by ![]() and
and ![]()
Note that
| (5) |
Introduce the notation:
 |
With the help of equalities (1)-(5) we can
obtain expressions for the members
of the sequences ![]()
![]()
![]()
![]()
![]() and
and ![]()
3. Distribution of the number of customers in the system during the busy period
Let ![]() be the number of customers in the system at time
be the number of customers in the system at time ![]() Denote by
Denote by ![]() (
(![]() ) the conditional probability, provided
that at the initial time the number
of customers of the system is equal to
) the conditional probability, provided
that at the initial time the number
of customers of the system is equal to ![]() and
the service begins with the service time distributed according to the law
and
the service begins with the service time distributed according to the law ![]()
![]()
Let ![]() denote
the length of the first busy period for the considered queueing system, and for
denote
the length of the first busy period for the considered queueing system, and for
![]()
 |
It is
evident that ![]()
![]() With the help of the formula
of total probability we obtain the equalities:
With the help of the formula
of total probability we obtain the equalities:
 | (6) |
Here ![]() is the indicator of
a random event
is the indicator of
a random event ![]() ; it equals 1 or 0 depending
on whether or not the event
; it equals 1 or 0 depending
on whether or not the event ![]() occurs.
occurs.
Introduce the notation:
Taking into account the relations (1) and (2),
from (6) we obtain the system of equations for the functions ![]() and
and ![]() :
:
| (7) |
| (8) |
with the boundary conditions
| (9) |
For solving the systems of equations (7)-(9)
we will use the functions ![]() and
and ![]() defined by the recurrence
relations:
defined by the recurrence
relations:
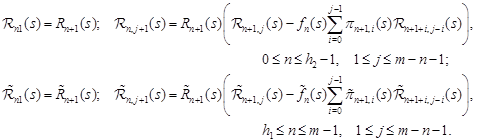 | (10) |
Introduce the notation:
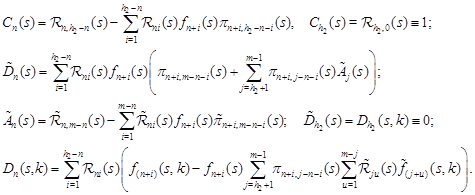 |
Reasoning as in the proof of Theorem 1 of [7], we obtain the following statement.
Theorem 1. For all ![]() and
and ![]() the
equalities
the
equalities
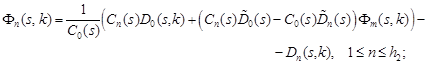 |
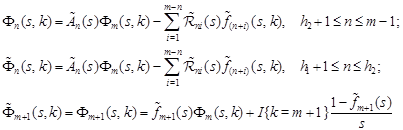
are fulfilled, where
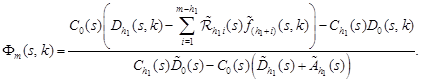 |
4. Busy period and stationary distribution
If the system starts functioning at the moment when the first customer arrives, then
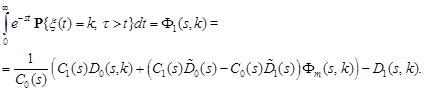 | (11) |
To obtain
a representation for ![]() we sum up equalities (11) for
we sum up equalities (11) for ![]() running from 1 to
running from 1 to ![]() . Given the
definitions of
. Given the
definitions of ![]()
![]()
![]() and
and ![]() it
is not difficult to ascertain that
it
is not difficult to ascertain that
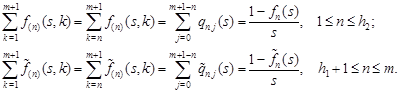 |
Introduce the notation:
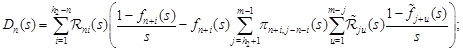
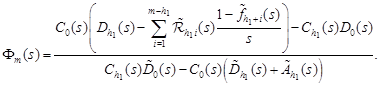 |
Thus, (11) confirms the following statement.
Theorem 2. The Laplace transform of the distribution function of the length of the busy period is defined as
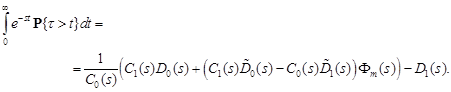 | (12) |
To find ![]() we need to pass to the limit in (12) as
we need to pass to the limit in (12) as ![]() We use the sequences
We use the sequences ![]()
![]()
![]() and
and ![]() as well as
sequences
as well as
sequences ![]() and
and ![]() obtained by
limit passages:
obtained by
limit passages: ![]()
![]() For
For ![]() and
and ![]() (10) implies the recurrence relations:
(10) implies the recurrence relations:
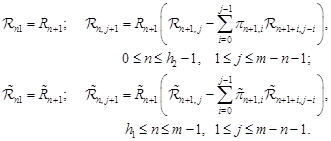 | (13) |
Note that ![]()
Using the relations (13) and taking into account the equalities
we can prove that
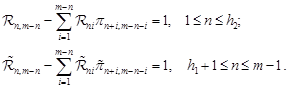 | (14) |
Given (5) and (14), using (12) we obtain the following statement.
Theorem 3. The mean length of the busy period is determined in the form
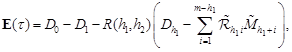 | (15) |
where
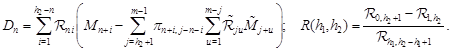 |
Introduce
the notation: ![]()
![]() Reasoning as in the paper [4],
from (11) we obtain formulas for the stationary distribution
of the number of customers in the system.
Reasoning as in the paper [4],
from (11) we obtain formulas for the stationary distribution
of the number of customers in the system.
Theorem 4. The stationary distribution of the number of customers in the system is given by
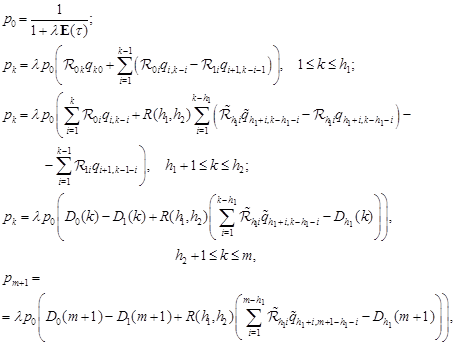 | (16) |
where
Using (15) we find the ratio of the mean number of customers served per unit of time to the mean number of all arriving customers per unit time and obtain the formula for the stationary service probability
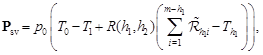 | (17) |
where
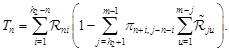 |
We find the
stationary queue characteristics - the average queue length ![]() and average waiting time
and average waiting time ![]() - by the formulas
- by the formulas
| (18) |
5. Example for calculating of stationary characteristics
Assume that ![]()
![]()
![]()
![]()
![]() the uniform
distribution on the intervals
the uniform
distribution on the intervals ![]() and
and ![]() corresponds to the distribution
functions of the service time
corresponds to the distribution
functions of the service time ![]() and
and ![]()
![]() respectively.
Thus,
respectively.
Thus,
The row ![]() of Table 1 contains steady-state
probabilities
of Table 1 contains steady-state
probabilities ![]() calculated by the formulas
(16). For the sake of comparison, the same table contains the corresponding
probabilities evaluated by the GPSS World simulation system [11, 12]
for the time value
calculated by the formulas
(16). For the sake of comparison, the same table contains the corresponding
probabilities evaluated by the GPSS World simulation system [11, 12]
for the time value ![]() The values of the stationary
characteristics found by
the formulas (15), (17) and (18), and calculated with the help of GPSS World,
are shown in Table 2.
The values of the stationary
characteristics found by
the formulas (15), (17) and (18), and calculated with the help of GPSS World,
are shown in Table 2.
Table 1
Stationary distribution of the number of customers in the system
|
Number of customers k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
pk |
0.00373 |
0.01504 |
0.05757 |
0.13005 |
0.24539 |
0.33756 |
0.15697 |
0.05369 |
|
pk (GPSS World) |
0.00371 |
0.01506 |
0.05768 |
0.13005 |
0.24527 |
0.33713 |
0.15693 |
0.05418 |
Table 2
Stationary characteristics of the system
|
Characteristic |
E(t) |
E(Q) |
E(W) |
Psv |
|
Analytical value |
26.724 |
3.511 |
0.541 |
0.650 |
|
Value according to GPSS World |
26.894 |
3.512 |
0.541 |
0.649 |
Calculations show that if the random dropping
of customers is not used, then
for the considered data the value of the capacity of the system ![]() is increased by 13.1%, but
is increased by 13.1%, but ![]() and
and ![]() are also increased
by 25.6% and 11.1% respectively.
are also increased
by 25.6% and 11.1% respectively.
6. Conclusions
With the help of the potentials method, we
have obtained simple and suitable formulas for numerical realization for
finding the stationary characteristics of the ![]() queueing system with the random dropping of customers and hysteretic
change of the service time. We have examined a fairly general statement of the
problem, because we assume that the service time depends on the number of
customers in the system and the dropping probability is a function of the queue
length at the time of arrival of a customer.
queueing system with the random dropping of customers and hysteretic
change of the service time. We have examined a fairly general statement of the
problem, because we assume that the service time depends on the number of
customers in the system and the dropping probability is a function of the queue
length at the time of arrival of a customer.
Our approach, unlike most of the methods used to study the semi-Markov models of queueing, allows to investigate not only stationary, but also the transient regime of the system, in particular, to find the Laplace transforms for the distribution of the number of customers in the system during the busy period and for the distribution function of the length of the busy period.
References
[1] Chydziński A., Nowe modele kolejkowe dla węzłów sieci pakietowych, Pracownia Kompute- rowa Jacka Skalmierskiego, Gliwice 2013.
[2] Tikhonenko O., Kempa W.M., Queue-size distribution in M/G/1-type system with bounded capacity and packet dropping, Communications in Computer and Information Science 2013, 356, 177-186.
[3] Kempa W.M., A direct approach to transient queue-size distribution in a finite-buffer queue with AQM, Applied Mathematics and Information Sciences 2013, 7, 3, 909-915.
[4] Zhernovyi K.Yu., Zhernovyi Yu.V., Mq/G/1/m and Mq/G/1 systems with the service time dependent on the queue length, Journal of Communicat. Technology and Electronics 2013, 58, 12, 1267-1275.
[5] Zhernovyi Yu., Zhernovyi K., Potentials Method for Threshold Strategies of Queueing, LAP Lambert Academic Publishing, Saarbrücken 2015 (in Russian).
[6] Zhernovyi K.Yu., Stationary characteristics of the Mq/G/1/m system with the threshold functioning strategy, Journal of Communicat. Technology and Electronics 2011, 56, 12, 1585-1596.
[7] Zhernovyi Yu., Kopytko B., The potentials method for a closed queueing system with hysteretic strategy of the service time change, Journal of Applied Mathematics and Computational Mechanics 2015, 14(2), 131-143.
[8] Zhernovyi Yu.V., Zhernovyi K.Yu., Method of potentials for a closed system with queue length dependent service times, J. of Communicat. Technology and Electronics 2015, 60, 12, 1341-1347.
[9] Zhernovyi Yu., Kopytko B., Zhernovyi K. On characteristics of the Mq/G/1/m and Mq/G/1 queues with queue-size based packet dropping, Journal of Applied Mathematics and Computational Mechanics 2014, 13(4), 163-175.
[10] Wentzel E.S., Ovcharov L.A., Theory of Stochastic Processes and its Engineering Applications, Vysshaya Shkola, Moscow 2000 (in Russian).
[11] Zhernovyi Yu., Creating Models of Queueing Systems Using GPSS World, LAP Lambert Academic Publishing, Saarbrücken 2015.
[12] Boyev V.D., Systems Modeling, Tools of GPSS World, BHV-Petersburg, St. Petersburg 2004 (in Russian).

