An example of non-Keller mapping
Edyta Pawlak
,Sylwia Lara-Dziembek
,Grzegorz Biernat
,Magdalena Woźniakowska
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
AN EXAMPLE OF NON-KELLER MAPPING
Edyta Pawlak 1, Sylwia Lara-Dziembek 1, Grzegorz Biernat 1 Magdalena Woźniakowska 2
1
Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
2 Faculty of Mathematics and Computer Science, University of Lodz
Łódź, Poland
edyta.pawlak@im.pcz.pl, sylwia.lara@im.pcz.pl, grzegorz.biernat@im.pcz.pl
magdalena_wozniakowska@wp.pl
Abstract. In the paper a nontrivial example of non-Keller mapping is considered. It is shown that the Jacobian of rare mapping, having one zero at infinity, being constant must vanish.
Keywords: Jacobian, zero at infinity, rare mappings, Keller mappings
1. Introduction
In this paper we consider the rare polynomial
mappings of two complex
variables. We study the mappings having one zero at infinity [1-3]. We prove
that if the Jacobian of this mapping is constant, it must be zero. The work
concerns the problems related to the Keller mappings [4-6]. Recall that the
Keller mapping
is a polynomial mapping ![]() satisfies the condition
satisfies the condition ![]() .
In this work, non-Keller
mapping are those whose the Jacobian being constant must vanish.
.
In this work, non-Keller
mapping are those whose the Jacobian being constant must vanish.
2. The rare mappings
Let ![]() be the complex polynomials of degrees 2k + 1
and 2k,
consequently, and having one zero at infinity. We
consider the rare mappings, i.e. the mappings, whose number of zero forms
following the leading form is not more than k – 1.
In our case, the mapping has exactly k – 1 zero
forms.
be the complex polynomials of degrees 2k + 1
and 2k,
consequently, and having one zero at infinity. We
consider the rare mappings, i.e. the mappings, whose number of zero forms
following the leading form is not more than k – 1.
In our case, the mapping has exactly k – 1 zero
forms.
Therefore, we can write
| (1) |
and
| (2) |
where ![]() and
and ![]() are the forms indicated degrees.
are the forms indicated degrees.
3. Basic lemma
At the beginning let us provide the following property:
Property. If ![]() , then
, then
![]() .
.
Proof.
Must be
| (3) |
Therefore
| (4) |
and since ![]() , so
, so ![]()
We assume
| (5) |
Let’s prove that ![]()
Lemma. Really,
with the given assumptions, we have ![]()
Proof. Let
 | (6) |
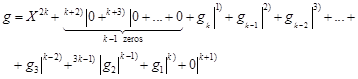 | (7) |
Since the Jacobian is constant, we have in sequence
| (8) |
so
| (9) |
and next
| (10) |
therefore
| (11) |
and
| (12) |
however
| (13) |
etc.
Finally in the step k) we have
| (14) |
so
| (15) |
Now, an important step
| (16) |
where according to the formula (9) we have
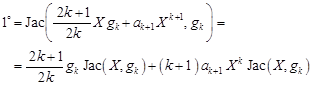 | (17) |
Returning to the formula (16) we obtain
| (18) |
then
| (19) |
This means that
| (20) |
so, according to the Property, we obtain
| (21) |
and reusing the formula (19) we have
| (22) |
In the next step we receive
| (23) |
where according to the formulas (21) and (11) we get
| (24) |
and
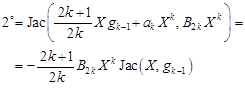 | (25) |
Returning to the formula (23) we have
| (26) |
Let’s
| (27) |
We consider two cases:
(I)
![]()
Then
| (28) |
In the next steps we receive in sequence
| (29) |
so
| (30) |
etc.
Finally, in the step 2k) we have
| (31) |
Thus, according to the formula (22) we obtain
| (32) |
what concludes the proof in the first case.
(II)
![]()
Then in the step k + 3) we get
| (33) |
So using the formulas (11), (13), (21) and (28) we have
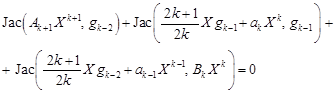 | (34) |
hence
| (35) |
and
| (36) |
therefore
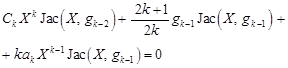 | (37) |
Because Ck = 0, then
| (38) |
Consequently
| (39) |
In the following steps, depending on the obtained values of the coefficients (non-zero or zero), we obtain the successive values of the forms
| (40) |
When all the subsequent coefficients are zero, in step 3k – 1) we have
| (41) |
Thus, according to the formula (22) we obtain
| (42) |
which ends the proof in the second case.
4. Conclusion
In this article we consider the “frontier” case of rare and non-Keller mapping. Increasing the number of zeros trivializes the calculation and the reduction significantly complicates them. Even so, we believe that we can reduce the number of zeros.
Algorithms reducing the number of zeros seem to be difficult, as we mentioned earlier. It is sufficient to consider the case when the number of zeros equals k – 2. The algorithms reducing the number of zeros will be presented in future articles.
References
[1] Griffiths P., Harris J., Principles of Algebraic Geometry, New York 1978.
[2] Mumford D., Algebraic Geometry I: Complex Projective Varieties, Springer-Verlag, New York 1975.
[3] Shafarevich I.R., Basic Algebraic Geometry, Springer-Verlag, Berlin, New York 1974.
[4] Wright D., On the Jacobian conjecture, Illinois J. Math. 1981, 25, 3, 423-440.
[5] Van den Essen A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathe- matics 190, Birkhäuser Verlag, Basel 2000.
[6] Bass H., Connell E.H., Wright D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, American Mathematical Society. Bulletin. New Series 1982, 7(2), 287-330.

