Certain inequalities connected with the golden ratio and the Fibonacci numbers
Marcin Adam
,Bożena Piątek
,Mariusz Pleszczyński
,Barbara Smoleń
,Roman Wituła
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
CERTAIN INEQUALITIES CONNECTED WITH THE GOLDEN RATIO AND THE FIBONACCI NUMBERS
Marcin Adam, Bożena Piątek, Mariusz Pleszczyński, Barbara Smoleń[*], Roman Wituła
Institute of Mathematics, Silesian
University of Technology
Gliwice, Poland
marcin.adam@polsl.pl, bozena.piatek@polsl.pl, mariusz.pleszczynski@polsl.pl, roman.witula@polsl.pl
Abstract. In the present paper we give some condensation type inequalities connected with Fibonacci numbers. Certain analytic type inequalities related to the golden ratio are also presented. All results are new and seem to be an original and attractive subject also for future research.
Keywords: Fibonacci numbers, golden ratio, Perrin constant
1. Introduction
The notion of Fibonacci numbers and the golden ratio may be found in many branches of mathematics, including number theory, geometry, algebra, matrix theory, numerical methods, classical analysis, dynamical systems, and even spectral analysis or music (see monographs [1-3], and selective papers [4-7]). Despite such a large spread occurrence of Fibonacci numbers and the golden ratio in mathematics, still some areas of mathematics tend to be poorly represented by these objects. In our opinion, a good example of such a niche (considered also in this paper) is the area of analytic inequalities. We believe this paper opens up a new stage of discoveries, and the inequalities presented here will be classical ones in the considered area of mathematics.
The main results of the paper are presented in two sections. In the first one we investigated the condensation type inequalities associated with the Fibonacci numbers. In the second one we discuss several analytic type inequalities related to the golden ratio and Perrin constant.
2. Condensation type inequalities connected with Fibonacci numbers
We begin with the following inequality based on basic properties of the Fibonacci numbers. Let us recall that the Fibonacci numbers are defined by the following linear recurrence relation
with ![]() . As a
result of the definition we get
. As a
result of the definition we get ![]() .
.
Theorem 1. Let
![]() and
and ![]() be a finite sequence of real numbers such that two inequalities
are satisfied:
be a finite sequence of real numbers such that two inequalities
are satisfied:
1.
| (1) |
2.
| (2) |
Then there is an index ![]() such
that
such
that
Proof. We prove this by contradiction. Let us suppose that for each index ![]() we have
we have
| (3) |
which immediately leads to the following inequality
| (4) |
that can be easily shown by induction. Indeed, from (3) we have
for the initial step and
for the inductive one.
From (4), on account of (1) we obtain
Next, let us denote ![]() where
where ![]() Then the
left-hand side of the previous inequality is equal to the following:
Then the
left-hand side of the previous inequality is equal to the following:
Now from (2) it follows directly that ![]() for all
for all ![]() Indeed,
Indeed, ![]() and since
and since
![]() , there is
, there is
![]() So
finally we obtain
So
finally we obtain
which contradicts to (4). This completes the proof.
As a direct conclusion of this result we obtain the following generalization:
Corollary 2. Let ![]() and
and ![]() be a finite sequence of
real numbers satisfying condition 1 of the
previous theorem. If, additionally,
be a finite sequence of
real numbers satisfying condition 1 of the
previous theorem. If, additionally,
for some ![]() then
there is an index
then
there is an index ![]() such
that
such
that
Remark 3. For the inequality (2) see also Chern and Cui paper [8].
3. Inequalities connected with the golden ratio
Let ![]() denote
the golden ratio, i.e.
denote
the golden ratio, i.e. ![]() and let
and let ![]()
![]() .
.
Theorem 4. The following golden ratio type inequalities hold:
1.
for ![]() ; the
equality sign is attained for
; the
equality sign is attained for ![]() only. The
function
only. The
function ![]() is
increasing on interval
is
increasing on interval ![]() and
decreasing on each of the intervals
and
decreasing on each of the intervals ![]() and
and ![]() , where
, where ![]() (see Fig.
1). We note that
(see Fig.
1). We note that
2. The function
is increasing on each
of the intervals ![]() and
and ![]() , and decreasing on
interval
, and decreasing on
interval ![]() , where
, where ![]() . We note
that
. We note
that ![]() and
and
3. The function
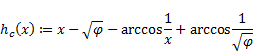 |
is decreasing on ![]() and
increasing on
and
increasing on ![]() .
.
Moreover, we have ![]() .
.
4. Let us set
for ![]() , and
, and
for ![]() . Then the
function
. Then the
function ![]() is
increasing on each of
intervals
is
increasing on each of
intervals ![]() and
and ![]() , and decreasing on interval
, and decreasing on interval ![]() . On the
other hand, the function
. On the
other hand, the function ![]() is
increasing on each of the intervals
is
increasing on each of the intervals ![]() and
and ![]() , and decreasing
on
, and decreasing
on ![]() Furthermore
we obtain
Furthermore
we obtain
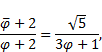 |
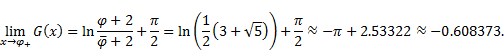 |
Moreover, if ![]() then (see
Figs. 2-4)
then (see
Figs. 2-4)
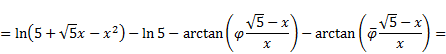 |
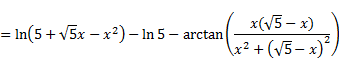 |
and the minimum of this function is attained in ![]() , we have
, we have
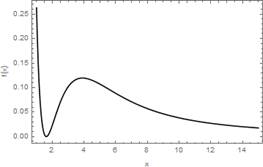
Fig. 1. Plot of the function ![]()
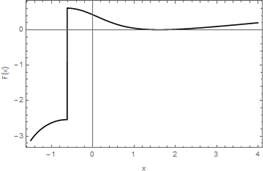
Fig. 2. Plot of the function ![]()
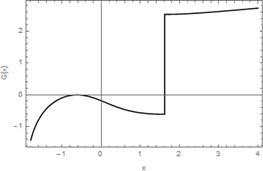
Fig. 3. Plot of the function ![]()
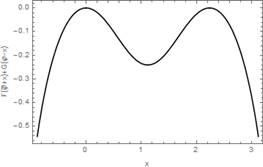
Fig. 4. Plot of the function ![]() in the
interval
in the
interval ![]() (the domain of this one is equal to
(the domain of this one is equal to ![]()
Proof. We consider the following functions:
Computing derivatives of these functions we obtain
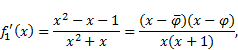 |
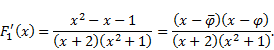 |
Moreover,
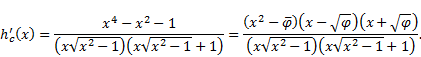 |
It is easy to check that the function ![]() is
decreasing on
is
decreasing on ![]() and is
increasing on
and is
increasing on ![]() , so we
have
, so we
have ![]() for
for ![]() which is equivalent to the inequality
which is equivalent to the inequality ![]() for
for ![]() (the equality sign is attained here only for
(the equality sign is attained here only for ![]() ).
By numerical calculations, we proved that the function
).
By numerical calculations, we proved that the function ![]() is increasing on interval
is increasing on interval ![]() and
decreasing on intervals
and
decreasing on intervals ![]() and
and ![]() , where
, where ![]() .
.
Similarly as ![]() , also
, also ![]() is
decreasing on
is
decreasing on ![]() and is
increasing on
and is
increasing on ![]() , so we
obtain
, so we
obtain
i.e.
We have ![]() . By
numerical calculations we proved that the function
. By
numerical calculations we proved that the function ![]() is
increasing on intervals
is
increasing on intervals ![]() and
and ![]() , and decreasing on interval
, and decreasing on interval ![]() . The
function
. The
function ![]() is
decreasing on
is
decreasing on ![]() ) and
increasing on
) and
increasing on ![]() . Hence,
function
. Hence,
function ![]() has a
local minimum at the point
has a
local minimum at the point ![]() which is
equal to
which is
equal to ![]() .
.
Corollary 5. By item 1, the following inequality holds
In equivalent form, we obtain
| (5) |
Proof. We have
i.e.
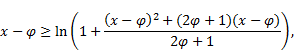 |
which implies (5) for ![]() since
since ![]() and
and ![]() .
.
Corollary 6. By item 2, the following inequality holds
Corollary 7. By item 3, the following inequality holds
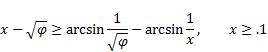 |
More precisely, the function
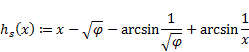 |
is decreasing on interval ![]() and
increasing on interval
and
increasing on interval ![]() .
.
Remark 8. Closely
connected to the golden ratio is the so-called Perrin constant ![]() defined
to be the only real zero of the so-called Perrin polynomial (see [9-11])
defined
to be the only real zero of the so-called Perrin polynomial (see [9-11])
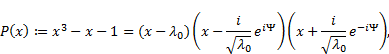 |
where
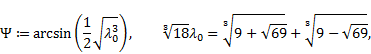 |
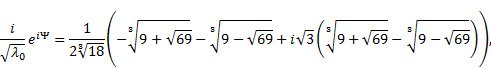 |
and ![]() .
.
In relation to inequalities
and
from point 4 of Theorem 4, we are interested in
the equivalent of these inequalities for the Perrin constant ![]() , i.e. the
inequalities of the type
, i.e. the
inequalities of the type
where
Since we have
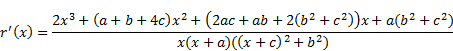 |
so we are interested when the following system of equations hold:
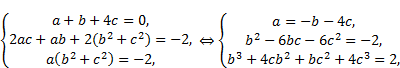 | (6) |
which implies that ![]() is a real solution of the following equation
is a real solution of the following equation
i.e.
Finally, by numerical calculations we get precisely two triplets of real numbers being the solution of system (6):
1) ![]() ,
,
2) ![]() .
.
For these solutions we can deduce the following inequalities:
A) the first collection of five inequalities for the first triple (a, b, c) of solutions (see Fig. 5)
where
and
| Λ |
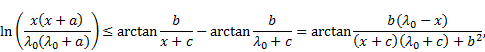 |
for ![]() and
where the equality sign is taken only for
and
where the equality sign is taken only for ![]() .
.
The function
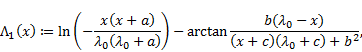 |
is increasing on ![]() ,
, ![]() .
Moreover,
.
Moreover, ![]() is
decreasing on two intervals
is
decreasing on two intervals ![]() and
and ![]() , and
, and
B) for the second triple (a, b, c) of solutions similar inequalities can be obtained, however, due to the volume of the paper, they will be omitted.
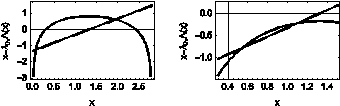
Fig. 5. Plot of
the functions ![]() and
and ![]() for the
first triple
for the
first triple ![]() - on the
left,
and for the second triple
- on the
left,
and for the second triple ![]() - on the
right
- on the
right
4. Conclusions
In the paper certain inequalities connected with the golden ratio and the Fibonacci numbers are discussed. We were able to accomplish the intended overall goal of the paper, even with some excess (see in particular the results of point 4 of Theorem 4). Generalization from Remark 8 connected with the Perrin’s polynomial and constant is quite natural and in fact well-defined, but did not completely fulfill our expectations of aesthetic nature. We believe that the research subject matter indicated in this paper is still open and can encourage (especially Fibomaniacs) for active reflection.
References
[1] Dunlop R., The Golden Ratio and Fibonacci Numbers, World Scientific, Singapore 2006.
[2] Vajda S., Fibonacci and Lucas Numbers, and the Golden Section Theory and Applications, Dover Publications Inc., New York 2008.
[3] Hoggatt V.E., Fibonacci and Lucas Numbers, The Fibonacci Association, Santa Clara 1979.
[4] Mongoven C., Sonification of multiple Fibonacci-related sequences, Annales Mathematicae et Informaticae 2013, 41, 175-192.
[5] Wituła R., Słota D., Hetmaniok E., Bridges between different known integer sequences, Annales Mathematicae et Informaticae 2013, 41, 255-263.
[6] Słanina P., Generalizations of Fibonacci polynomials and free linear groups, Linear and Multilinear Algebra, DOI: 10.1080/03081087.2015.1031073.
[7] Herz-Fischler R., A “very pleasant” theorem, College Mathematics Journal 1993, 24, 4, 318-324.
[8] Chern S., Cui A., Fibonacci numbers close to a power of 2, The Fibonacci Quarterly 2014, 52, 4, 344-348.
[9] Hetmaniok E., Wituła R., Lorenc P., Pleszczyński M., On an improvement of the numerical application for Cardano’s formulae in Mathematica software (in review).
[10] Wituła R., Lorenc P., Różański M., Szweda M., Sums of the rational powers of roots of cubic polynomials, Zeszyty Naukowe Politechniki Śląskiej, Seria Matematyka Stosowana 2014, 4, 17-34.
[11] Dubickas A., Hare K.G., Jankauskas J., There are no two nonreal conjugates of a Pisot number with the same imaginary part, arXiv:1410.1600v1 [math.NT].
[*] Currently, the fourth author, Barbara Smoleń, is a student of mathematics and this paper is a part of her Bachelor's thesis written under the supervision of Prof. Roman Wituła.

