Multi-layer neural networks for sales forecasting
Magdalena Scherer
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Scherer_2018,
doi = {10.17512/jamcm.2018.1.06},
url = {https://doi.org/10.17512/jamcm.2018.1.06},
year = 2018,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {17},
number = {1},
pages = {61--68},
author = {Magdalena Scherer},
title = {Multi-layer neural networks for sales forecasting},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2018.1.06 UR - https://doi.org/10.17512/jamcm.2018.1.06 TI - Multi-layer neural networks for sales forecasting T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Scherer, Magdalena PY - 2018 PB - The Publishing Office of Czestochowa University of Technology SP - 61 EP - 68 IS - 1 VL - 17 SN - 2299-9965 SN - 2353-0588 ER -
Scherer, M. (2018). Multi-layer neural networks for sales forecasting. Journal of Applied Mathematics and Computational Mechanics, 17(1), 61-68. doi:10.17512/jamcm.2018.1.06
Scherer, M., 2018. Multi-layer neural networks for sales forecasting. Journal of Applied Mathematics and Computational Mechanics, 17(1), pp.61-68. Available at: https://doi.org/10.17512/jamcm.2018.1.06
[1]M. Scherer, "Multi-layer neural networks for sales forecasting," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 1, pp. 61-68, 2018.
Scherer, Magdalena. "Multi-layer neural networks for sales forecasting." Journal of Applied Mathematics and Computational Mechanics 17.1 (2018): 61-68. CrossRef. Web.
1. Scherer M. Multi-layer neural networks for sales forecasting. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(1):61-68. Available from: https://doi.org/10.17512/jamcm.2018.1.06
Scherer, Magdalena. "Multi-layer neural networks for sales forecasting." Journal of Applied Mathematics and Computational Mechanics 17, no. 1 (2018): 61-68. doi:10.17512/jamcm.2018.1.06
MULTI-LAYER Neural Networks FOR SALES FORECASTING
Magdalena Scherer
Department of Engineering Management,
Czestochowa University of Technology
Czestochowa, Poland
magdalena.scherer@wz.pcz.pl
Received: 5 December 2017;
Accepted: 14 February 2018
Abstract. Predicting business operations on the basis of previous events plays an important role in managing a company. In the paper, we predict monthly sales volume of a textile warehouse by mathematical tools. To this end we use a feedforward artificial neural network trained on past data. The network predicted the volume with high accuracy. For the examined company, such prediction is very important as nearly the entire range of products is imported from different countries and the goods have to be ordered in advance.
MSC 2010: 68T05, 60G25
Keywords: data forecasting, machine learning, artificial neural networks
1. Introduction
Forecasting and the ability to assess future events play a key role in business operations. The uncertainty of the future and the time interval, from the moment of the decision to its result, makes it necessary to find appropriate prognostic methods, which are burdened with the smallest error and are simple and inexpensive to use. With increasingly accurate forecasting, decision making becomes much easier, making enterprise management easier. Forecasts should be the basis for creating business action plans. Still, new methods of forecasting are being sought, where the results will be as accurate as possible, and the methods will be relatively simple and cheap to use. Forecast-based management is applied in companies to manage production [1], sales or reverse logistics [2]. Moreover, it is used to credit risk management in banks [3], predicting the success of bank’s direct marketing [4], analyzing consumer loyalty [5], sport [6], medicine [7] and many other areas. Prediction can be performed by various tools such as learning vector quantization [8], neuro-fuzzy systems [9], data stream classifiers [10], energy-associated tuning [11] or deep neural networks [12]. In the case where part of data is missing we can use rough set-based systems [13]. The data used for the forecast have been made available by one of the companies that imports and sell textiles. The sales forecast is particularly important for this company because most materials are imported and orders are placed well in advance.
2. Methodology of the research
To predict the sale volume, we use artificial neural networks, which are mathematical structures and their software or hardware models. The inspiration for their construction was the natural neurons connected by synapses and the entire nervous system, and in particular its central point - the brain. Artificial neural networks can be used in a broad spectrum of data processing issues, such as pattern classification, prediction, denoising, compression and image and sound recognition, or automation.
Neural networks have the ability to process incomplete data and to provide approximate results. They enable fast and efficient processing of large amounts of data. They are resistant to errors and damage.

Fig. 1. Artificial neuron model
The basic element of the neural network is
the neuron [14]. Figure 1 shows
the neuron model, where ![]() is the number of inputs to the
neuron,
is the number of inputs to the
neuron, ![]() are input signals,
are input signals, ![]() are synaptic weights,
are synaptic weights, ![]() is the output value,
is the output value, ![]() is bias and
is bias and ![]() is the activation function. The operation of the neuron can be
described using
the formula
is the activation function. The operation of the neuron can be
described using
the formula
| (1) |
where
| (2) |
The input
signals ![]() are multiplied by the corresponding weights
are multiplied by the corresponding weights ![]() The resulting values are summed to produce a signal s. The
signal is then subjected to an activation function that is usually nonlinear to
create many layers. There are many models of neural networks. The neural
network division can be made taking into account the following factors:
learning method, direction of signal propagation in the network, type of activation
function, type of input data and method of interconnection between neurons.
The resulting values are summed to produce a signal s. The
signal is then subjected to an activation function that is usually nonlinear to
create many layers. There are many models of neural networks. The neural
network division can be made taking into account the following factors:
learning method, direction of signal propagation in the network, type of activation
function, type of input data and method of interconnection between neurons.
Neural networks consist of interconnected neurons. Depending on how these connections are made, three types of neural networks are distinguished: feedforward, feedback networks, convolutional and cellular networks. In feedforward, one-way networks, the flow of signals is always in one direction, from the input to the output. Neuron outputs from one layer are neuron inputs in the next layer. On feedback networks, also known as recursive, some of the output signals are simultaneously input signals. In networks of this type, the activation of the network by the input signal causes the activation of some or all of the neurons in the, so-called, network relaxation process. Therefore, in order to validate the operation of the network, a stability condition should be added. The stimulated network must reach a stable state where the baseline values of the neurons remain constant. This process should take place at a finite time. On the other hand, in cellular neural networks, each neuron is connected to neighbouring neurons.
Most commonly used neural architecture, both
in research and commercial models, are perceptron networks. These are
unidirectional networks where neurons are grouped in at least two layers. The
first layer is called the input layer and the last layer is the output layer.
There may be one or more hidden layers between these layers. Signals are passed
from the input layer to the output layer, without feedback to the previous
layers. The diagram of the three-layer neural network
is shown in Figure 2, where ![]() denote input signals. In a
general case, we can have more than one output signal,
denote input signals. In a
general case, we can have more than one output signal, ![]() and several layers denoted
by k. The error Q at the network output
is defined by
and several layers denoted
by k. The error Q at the network output
is defined by
| (3) |
where t is the iteration number, d is a desired value, y is the output of ith neuron defined by
| (4) |
where w is a weight. The backpropagation algorithm propagates error toward the network input, thus the error in hidden layers is defined as a sum of error in the next layer’s neurons weighted by corresponding weights
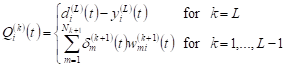 , , | (5) |
where ![]() is defined as multiplication of errors in the next layer and
the derivative of the activation function
is defined as multiplication of errors in the next layer and
the derivative of the activation function
| (6) |
where
| (7) |
Finally, we obtain the formula for weight modification in iteration t
| (8) |
where ![]() is the learning coefficient responsible for the convergence speed.
is the learning coefficient responsible for the convergence speed.
The number of neurons in each layer is important in the operation of the network. Too many neurons increase the learning process. In addition, if the number of learning samples in relation to network size is small, the network can be overtrained and thus lose the ability to generalize knowledge. In this case, the network will learn the learning dataset “by heart” and will probably correctly map only the samples that were included in it. Therefore, after learning the network, we should check the correctness of its operation. For this purpose, a test dataset consisting of samples that were not present in the network learning process is used. Only after testing it is possible to tell whether the network has been properly trained and works properly.
There are two methods of learning neural networks: supervised learning and unsupervised learning. Network learning involves enforcing a specific neural network response to the input signals. That is why a very important moment in research is the right choice of the learning method. Supervised teaching, also called learning with a teacher, involves modifying weights so that the output signals are as close as possible to the desired values. Training data includes both input signal groups and desired values for responding to these signals. A special case of supervised learning is reinforcement learning, where the network is trained not to give exact values of the desired output signals, but only the information or whether it responds correctly. Unattended learning, called non-teacher learning, is a self-parsing study of dependence in a test set by a neural network. During training, the network receives no information about the desired response. Training data contains only a set of input signals. Networks with such action are called self-organizing or self-associative.
Neural networks can learn a broad spectrum of problems on the basis of data. They are better than traditional computer architectures in tasks that people perform naturally, such as image recognition or generalization of knowledge. Advances in computer technology and network learning algorithms have resulted in a steady increase in the complexity of tasks solved by neural networks. New architectures are also emerging, such as convolutional neural networks being able to classify hundreds of image classes.
Neural networks are used to solve different problems [15, 16]. However, every problem requires a proper network adaptation. An appropriate network topology, the number of neurons in layers, and the number of network layers must be selected. Next, we need to prepare a training and testing set. The network must be trained to learn first and then the correct operation of the network must be verified. In the next section we use artificial multilayer perceptron to predict monthly sales volume.
3. Experiments
This paper concerns forecasting sales volume in monthly intervals in a medium Polish company. The data from previous months were used to train a feedforward neural network (full-connected) with the backpropagation algorithm [17] in the Matlab Neural Network Toolbox. We performed experiments with networks of various sizes, i.e. different number of neurons in the hidden layer. Moreover, we experimented with various numbers of past data as the input. It transpired that the three past months are enough to predict the sale with relatively good accuracy. Thus, the network, presented in Figure 2, had three inputs, one hidden layer and one output neuron. During the experiments, we picked the best network to have 15 neurons in the hidden layer and one output neuron. After 40 epochs of training with the backpropagation algorithm we achieved RMSE error 3.34e-11. Figure 3 shows the training data, i.e. monthly sales volume in running meters. Because of the high accuracy achieved, the predicted volume plot coincides with the data thus it is not visible. Figure 4 shows the error plot during training for the best network.
|


Fig. 3. Training data, i.e. monthly sales volume
We achieved good prediction accuracy that allows one to use the outcome to increase the effectiveness of the company management. We predicted the sale volume in the following month on the basis of three previous months using the feedforward neural network trained by the backpropagation algorithm.

Fig. 4. Training error for neural network with 15 hidden neurons
4. Conclusions
The paper concerned forecasting sales volume in monthly intervals in a medium Polish company. The company imports a large amount of fabric monthly from several countries, thus the effectiveness of the logistics is crucial. In the paper, we use mathematical tools to forecast sales volume. The data from previous months were used to train the feedforward neural network (full-connected) with the backpropagation algorithm to predict the volume in the following month. We achieved very good prediction accuracy that allows one to use the outcome to increase the effectiveness of the company management in terms of logistics. The main drawback of the presented method is the lack of the interpretability of the trained neural network as it acts as a black box. One of the possible solutions could be the application of neuro-fuzzy systems [18, 19] which use intelligible fuzzy rules.
References
[1] Tao, R., Yuan, D.C., & Hu, G.H. (2014). BP neural network based animation production prediction. Applied Mechanics and Materials, 539, 475-478.
[2] Scherer, M. (2017). Waste flows management by their prediction in a production company. Journal of Applied Mathematics and Computational Mechanics, 16, 2, 135-144.
[3] Konovalova, N., Kristovska, I., & Kudinska, M. (2016). Credit risk management in commercial banks. Polish Journal of Management Studies, 13, 2, 90-100.
[4] Scherer, M., Smoląg, J., & Gawęda, A. (2016). Predicting Success of Bank Direct Marketing by Neuro-fuzzy Systems. 15th International Conference on Artificial Intelligence and Soft Computing. Part II (ICAISC 2016), Cham: Springer International Publishing, 570-576.
[5] Deliana, Y., & Rum, I.A. (2017). Understanding consumer loyalty using neural network. Polish Journal of Management Studies, 16, 2, 51-61.
[6] Surujlal, J., & Dhurup, M. (2017). Antecedents predicting coaches’ intentions to remain in sport organisations. Polish Journal of Management Studies, 16, 1, 234-247.
[7] Szarek, A., Korytkowski, M., Rutkowski, L., Scherer, R., & Szyprowski, J. (2012). Application of neural networks in assessing changes around implant after total hip arthroplasty. In International Conference on Artificial Intelligence and Soft Computing, Berlin: Springer, 335-340.
[8] Villmann, T., Bohnsack, A., & Kaden, M. (2017). Can learning vector quantization be an alternative to svm and deep learning? - Recent trends and advanced variants of learning vector quantization for classification learning. Journal of Artificial Intelligence and Soft Computing Research, 7, 1, 65-81.
[9] Scherer, R. (2009). Neuro-fuzzy relational systems for nonlinear approximation and prediction. Nonlinear Analysis, 71, e1420-e1425.
[10] Nikulin, V. (2016). Prediction of the shoppers loyalty with aggregated data streams. Journal of Artificial Intelligence and Soft Computing Research, 6, 2, 69-79.
[11] Rivero, C.R., Pucheta, J., Laboret, S., Sauchelli, V., & Patińo, D. (2017). Energy associated tuning method for short-term series forecasting by complete and incomplete datasets. Journal of Artificial Intelligence and Soft Computing Research, 7, 1, 5-16.
[12] Chang, O., Constante, P., Gordon, A., & Singana, M. (2017). A novel deep neural network that uses space-time features for tracking and recognizing a moving object. Journal of Artificial Intelligence and Soft Computing Research, 7, 2, 125-136.
[13] Korytkowski, M., Nowicki, R., Rutkowski, L., & Scherer, R. (2011). AdaBoost Ensemble of DCOG Rough-Neuro-Fuzzy Systems, In Computational Collective Intelligence, Technologies and Applications, P. Jedrzejowicz, N. Nguyen, K. Hoang, Eds., Berlin/Heidelberg: Springer, 62-71.
[14] Bishop, Ch.M. (1995). Neural Networks for Pattern Recognition. Oxford University Press.
[15] Ke, Y., & Hagiwara, M. (2017). An English neural network that learns texts, finds hidden knowledge, and answers questions. Journal of Artificial Intelligence and Soft Computing Research, 7, 4, 229-242.
[16] Bologna, G., & Hayashi, Y. (2017). Characterization of symbolic rules embedded in deep DIMLP networks: a challenge to transparency of deep learning. Journal of Artificial Intelligence and Soft Computing Research, 7, 4, 265-286.
[17] Rumelhart, D.E., Hinton, G.E., & Williams, R.J. (1986). Learning representations by back-pro- pagating errors, Nature. 323, 6088, October, 533-536.
[18] Scherer, R. (2012). Multiple Fuzzy Classification Systems. Springer.
[19] Scherer, R, & Rutkowski, L. (2002), Neuro-Fuzzy Relational Systems. International Conference on Fuzzy Systems and Knowledge Discovery, Singapore, 44-48.


