Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method
Alicja Piasecka Belkhayat
,Anna Korczak
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Belkhayat_2017,
doi = {10.17512/jamcm.2017.4.06},
url = {https://doi.org/10.17512/jamcm.2017.4.06},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {4},
pages = {57--65},
author = {Alicja Piasecka Belkhayat and Anna Korczak},
title = {Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.4.06 UR - https://doi.org/10.17512/jamcm.2017.4.06 TI - Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Belkhayat, Alicja Piasecka AU - Korczak, Anna PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 57 EP - 65 IS - 4 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Belkhayat, A., & Korczak, A. (2017). Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method. Journal of Applied Mathematics and Computational Mechanics, 16(4), 57-65. doi:10.17512/jamcm.2017.4.06
Belkhayat, A. & Korczak, A., 2017. Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method. Journal of Applied Mathematics and Computational Mechanics, 16(4), pp.57-65. Available at: https://doi.org/10.17512/jamcm.2017.4.06
[1]A. Belkhayat and A. Korczak, "Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 4, pp. 57-65, 2017.
Belkhayat, Alicja Piasecka, and Anna Korczak. "Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method." Journal of Applied Mathematics and Computational Mechanics 16.4 (2017): 57-65. CrossRef. Web.
1. Belkhayat A, Korczak A. Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(4):57-65. Available from: https://doi.org/10.17512/jamcm.2017.4.06
Belkhayat, Alicja Piasecka, and Anna Korczak. "Modelling of transient heat transport in two-layered crystalline solid films using the interval lattice Boltzmann method." Journal of Applied Mathematics and Computational Mechanics 16, no. 4 (2017): 57-65. doi:10.17512/jamcm.2017.4.06
MODELLING OF TRANSIENT HEAT TRANSPORT IN TWO-LAYERED CRYSTALLINE SOLID FILMS USING THE INTERVAL LATTICE BOLTZMANN METHOD
Alicja Piasecka Belkhayat, Anna Korczak
Institute of Computational Mechanics and Engineering, Silesian University of Technology
Gliwice, Poland
alicja.piasecka@polsl.pl, anna.korczak@polsl.pl
Received: 6 December 2017;
Accepted: 28 December 2017
Abstract. In the paper, the numerical modelling of heat transfer in one-dimensional crystalline solid films is considered. A generalized two-layer problem is described by the Boltz- mann transport equations transformed in the phonon energy density equations supplemented by the adequate boundary-initial conditions. Such an approach in which the parameters appearing in the problem analysed are treated as the constant values is widely used, but in this paper the interval values of relaxation time and the boundary condition for silicon and diamond are taken into account. The problem formulated has been solved by means of the interval lattice Boltzmann method using the rules of directed interval arithmetic. In the final part of the paper the results of numerical computations are presented.
MSC 2010: 65M99, 80A20
Keywords: Boltzmann transport equation, interval lattice Boltzmann method, directed interval arithmetic
1. Introduction
In dielectric materials and semiconductors, the heat transport is mainly realized by a quanta of lattice vibrations called phonons. The phonons represent the conduction of heat and electricity through solids. In non-metals, phonons as heat carriers always “move” from the part with the higher temperature to the part with the lower temperature and, during this move, phonons carry energy. This kind of phenomena can be described by the Boltzmann transport equation (BTE). It should be pointed out that taking into account the extremely short duration and the domain dimensions expressed in nanometers, the macroscopic heat conduction equation based on the Fourier law cannot be used [1, 2]. Such an approach in which the parameters appearing in the mathematical model are treated as the constant values is widely used [3, 4]. Here, the interval values of relaxation times and boundary conditions for successive sub-domains are taken into account. The relaxation time is estimated experimentally, and its actual value is still a subject of discussion [5]. In the paper the heat transport proceeding in a two-layered thin film is considered [6-9]. To solve the problem formulated, the interval version of the lattice Boltzmann method is applied using the rules of directed interval arithmetic [10, 11]. In the final part of the paper the examples of numerical computations are shown.
2. Boltzmann transport equation
The unsteady BTE in a phonon energy density formulation using the simplifying assumptions of the Debye model for one-dimensional two-layered analysis [3, 12] can be written as
where s = 1, 2 corresponds to the successive layers of the thin
film (silicon, diamond), ![]() is the phonon energy density,
is the phonon energy density, ![]() is the equilibrium phonon energy density,
is the equilibrium phonon energy density, ![]() is the frequency-dependent phonon propagation
speed,
is the frequency-dependent phonon propagation
speed, ![]() is the frequency-dependent phonon relaxation time,
t denotes the time and
is the frequency-dependent phonon relaxation time,
t denotes the time and ![]() is the external heat generation rate related to a unit of volume.
is the external heat generation rate related to a unit of volume.
Using the Debye model, the dependence between phonon energy and lattice temperature can be calculated from the following formula
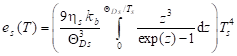 | (2) |
where ![]() is the Debye temperature of the
solid,
is the Debye temperature of the
solid, ![]() is the Boltzmann constant, Ts is the lattice temperature while
is the Boltzmann constant, Ts is the lattice temperature while ![]() is the number density of
oscillators [3].
is the number density of
oscillators [3].
The equations (1) should be supplemented by the boundary and initial conditions.
3. Interval lattice Boltzmann equation
The lattice Boltzmann method (LBM) is a numerical technique for the simulation of heat transfer. The LBM solves a discretized set of the BTE known as the lattice Boltzmann equations. The phonon energy density is defined as the sum
| (3) |
where ![]() is the phonon energy density in the positive x
direction for sth layer while
is the phonon energy density in the positive x
direction for sth layer while ![]() is the phonon energy density in
the negative x direction and d signifies the
lattice direction.
is the phonon energy density in
the negative x direction and d signifies the
lattice direction.
The interval Boltzmann transport equations for the one-dimensional problem take the form [13]
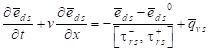 | (4) |
where ![]() is the component of velocity along the x-axis,
is the component of velocity along the x-axis, ![]() is the
lattice distance from site to
site,
is the
lattice distance from site to
site, ![]() is the time step needed for a
phonon to travel from one lattice site to the neighboring lattice site,
is the time step needed for a
phonon to travel from one lattice site to the neighboring lattice site, ![]() is the interval relaxation time and
is the interval relaxation time and ![]() .
.
The set of equations (4) must be supplemented by the boundary-initial conditions [6, 9]
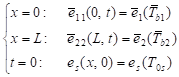 | (5) |
where ![]() and
and ![]() are the interval boundary temperatures and
are the interval boundary temperatures and ![]() is the initial temperature. Between the successive sub-domains the continuity
condition can be taken into account [9]
is the initial temperature. Between the successive sub-domains the continuity
condition can be taken into account [9]
| (6) |
The interval LBM algorithm has been used to solve the problem analysed [6, 10]. The approximate form of the equations (4) is of the following form
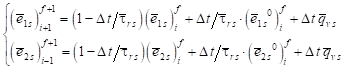 | (7) |
Taking into account the assumption that
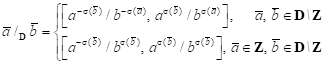 | (8) |
and
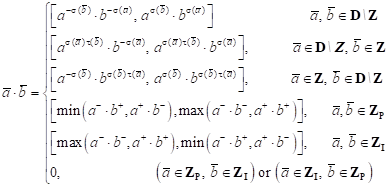 | (9) |
the product ![]() (s = 1, i = 3,
f = 4) is calculated
using the rules of
directed interval arithmetic according to the following
formula
(s = 1, i = 3,
f = 4) is calculated
using the rules of
directed interval arithmetic according to the following
formula
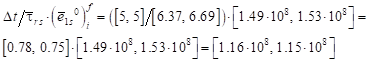 | (10) |
As a result, the interval obtained is improper.
After subsequent computations the interval lattice temperature is determined using the formula (see eq. (2))
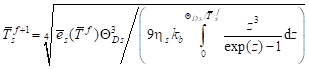 | (11) |
4. Results of computations
As a numerical
example, the heat transport in a silicon-diamond film of the
dimension L = 200 nm has been analysed. The following input data have been
introduced for a silicon-diamond film
respectively: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
Figure 1 illustrates the interval temperature
distribution in the domain considered for the chosen times. Figure 2 presents
the courses of the temperature function at the internal nodes ![]() nm (1) and
nm (1) and ![]() nm (2) for the silicon and
diamond layer respectively.
nm (2) for the silicon and
diamond layer respectively.
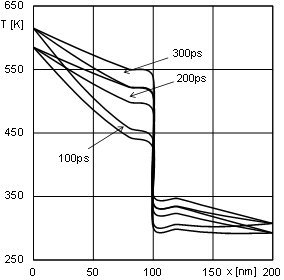
Fig. 1. The interval temperature distribution
In the second analysed example it is assumed
that the external heat
generation rate related to an unit of volume is the
interval number ![]()
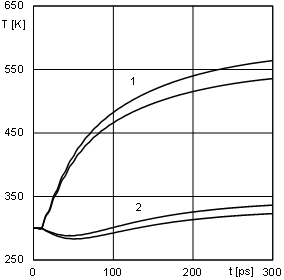
Fig. 2. The interval heating curves at internal nodes
Similar to the previous example, Figure 3 illustrates the interval temperature distribution in the domain considered for the chosen times, and Figure 4 presents the courses of the temperature function at the same internal nodes.
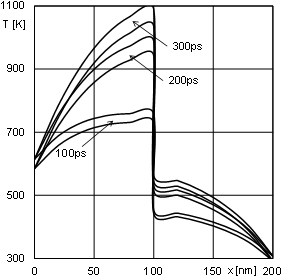
Fig. 3. The interval temperature distribution
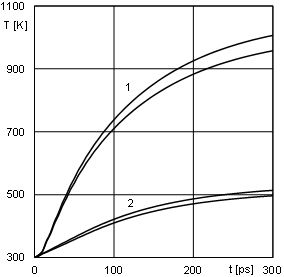
Fig. 4. The interval heating curves at internal nodes
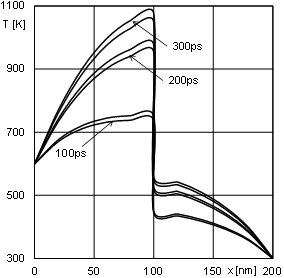
Fig. 5. The interval temperature distribution
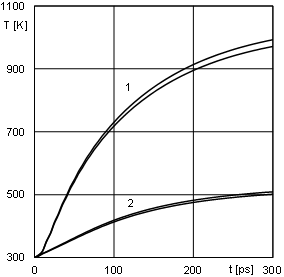
Fig. 6. The interval heating curves at internal nodes
In the last numerical example, accurate boundary
temperatures ![]() and
and ![]() have been introduced. In Figure 5, the interval temperature distribu-
tion in the domain considered for the chosen times are
shown and Figure 6 presents the courses of the temperature function at the same
internal nodes.
have been introduced. In Figure 5, the interval temperature distribu-
tion in the domain considered for the chosen times are
shown and Figure 6 presents the courses of the temperature function at the same
internal nodes.
It should be pointed out, that for each node of the domain considered there are two curves representing the beginning and end of temperatures intervals. The interval solution is illustrated by the area between these two curves.
Additionally one can see, that for longer calculation time, the temperature inter- vals are wider (see Figs. 2, 4 and 6). It is visible that a greater number of operations in the set of interval numbers impacts on the increase of the width of the obtained intervals.
5. Conclusions
In the paper a interval version of the lattice Boltzmann method for solving 1D problems in two-layered crystalline solid films has been presented. A model with interval values of relaxation times, boundary conditions and the external heat generation rate related to a unit of volume for a silicon-diamond film has been proposed.
The generalization of LBM allows one to find the numerical solution in the interval form, and such information may be important, especially for the parameters that are estimated experimentally, for example the relaxation time. The problem analysed can be extended to multi-layered thin films.
References
[1] Chen G., Borca-Tasciuc D., Yang R.G., Nanoscale heat transfer, [in:] Encycl. of Nanoscience and Nanotechnology, CA, American Scientific Publishers, Valencia, 7, 2004, 429-359.
[2] Smith A.N., Norris P.M., in Heat Transfer Handbook, A. Bejan, D. Kraus, Eds. 2003, 1309.
[3] Escobar R.A., Ghai S.S., Jhon M.S., Amon C.H., Multi-length and time scale thermal transport using the lattice Boltzmann method with application to electronics cooling, Journal of Heat and Mass Transfer 2006, 49, 97-107.
[4] Joshi A.A., Majumdar A., Transient ballistic and diffusive phonon heat transport in thin films, Journal of Applied Physics 1993, 74(1), 31-39.
[5] Narumanchi S., Murthy J.Y., Amon C.H., Simulation of unsteady small heat source effects in sub-micron heat conduction, Journal of Heat Transfer 2003, 123, 896-903.
[6] Ghai S.S., Kim W.T., Amon C.H., Jhon M.S., Transient thermal modeling of a nanoscale hot spot in multilayered film, Journal of Applied Physics 2006, 99.
[7] Majchrzak E., Mochnacki B., Suchy J.S., Numerical simulation of thermal processes proceeding in a multi-layered film subjected to ultrafast laser heating, Journal of Theoretical and Applied Mechanics 2009, 47, 2, 383-396.
[8] Majchrzak E., Mochnacki B., Greer A.L., Suchy J.S., Numerical modeling of short pulse laser interactions with multi-layered thin metal films, CMES: Computer Modeling in Engineering and Sciences 2009, 41, 2, 131-146.
[9] Pisipati S., Chen Ch., Geer J., Sammakia B., Murray B.T., Multiscale thermal device modeling using diffusion in the Boltzmann Transport Equation, International Journal of Heat and Mass Transfer 2013, 64, 286-303.
[10] Markov S.M., On directed interval arithmetic and its applications, Journal of Universal Computer Science 1995, 1, 514-526.
[11] Piasecka-Belkhayat A., Interval boundary element method for transient diffusion problem in two layered domain, Journal of Theoretical and Applied Mechanics 2011, 49, 1, 265-276.
[12] Escobar R.A., Smith B., Amon C.H., Lattice Boltzmann modeling of subcontinuum energy transport in crystalline and amorphous microelectronic devices, Journal of Electronic Packaging 2006, 128(2).
[13] Piasecka-Belkhayat A., Korczak A., Modelling of transient heat transport in one-dimensional crystalline solids using the interval lattice Boltzmann method, Recent Advances in Computational Mechanics, Taylor & Francis Group, A Balkema Book, London 2014, 363-368.


