One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer
Sebastian Garus
,Wojciech Sochacki
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Garus_2017,
doi = {10.17512/jamcm.2017.4.02},
url = {https://doi.org/10.17512/jamcm.2017.4.02},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {4},
pages = {17--27},
author = {Sebastian Garus and Wojciech Sochacki},
title = {One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.4.02 UR - https://doi.org/10.17512/jamcm.2017.4.02 TI - One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Garus, Sebastian AU - Sochacki, Wojciech PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 17 EP - 27 IS - 4 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Garus, S., & Sochacki, W. (2017). One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer. Journal of Applied Mathematics and Computational Mechanics, 16(4), 17-27. doi:10.17512/jamcm.2017.4.02
Garus, S. & Sochacki, W., 2017. One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer. Journal of Applied Mathematics and Computational Mechanics, 16(4), pp.17-27. Available at: https://doi.org/10.17512/jamcm.2017.4.02
[1]S. Garus and W. Sochacki, "One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 4, pp. 17-27, 2017.
Garus, Sebastian, and Wojciech Sochacki. "One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer." Journal of Applied Mathematics and Computational Mechanics 16.4 (2017): 17-27. CrossRef. Web.
1. Garus S, Sochacki W. One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(4):17-27. Available from: https://doi.org/10.17512/jamcm.2017.4.02
Garus, Sebastian, and Wojciech Sochacki. "One dimensional phononic FDTD algorithm and transfer matrix method implementation for Severin aperiodic multilayer." Journal of Applied Mathematics and Computational Mechanics 16, no. 4 (2017): 17-27. doi:10.17512/jamcm.2017.4.02
ONE DIMENSIONAL PHONONIC FDTD ALGORITHM AND TRANSFER MATRIX METHOD IMPLEMENTATION FOR SEVERIN APERIODIC MULTILAYER
Sebastian Garus, Wojciech Sochacki
Institute of Mechanics and Machine Design
Fundamentals, Czestochowa University of Technology
Czestochowa, Poland
gari.sg@gmail.com, w.sochacki@imipkm.pcz.pl
Received: 2 November 2017;
Accepted: 13 December 2017
Abstract. In this paper, the power spectrum and phononic properties of the quasi one-dimensional Severin aperiodic multilayer was investigated. Multilayer phononic structures with their phononic band gap properties can be used as filters of mechanical waves. In the paper, the implementation of the Finite Difference Time Domain (FDTD) algorithm with discrete Fourier transform and the Transfer Matrix Method algorithm in the Wolfram Language in Mathematica was made.
MSC 2010: 65M06, 65N06
Keywords: phononic, fdtd, transfer marix, aperiodic, multilayers
1. Introduction
The structure and geometry of amorphous phononic superlattices determines transmission properties of the analyzed structures - forbidden gaps can be observed [1, 2]. The band gap structure allows for the design of acoustic devices which can be used as acoustic/elastic filters, noise control or acoustic waveguides [3-7]. Some structures where the passband occurs into the band gap can be used for demultiplexing or as selective filters of acoustic wave [8, 9].
1.1. Finite Difference Time Domain algorithm
The Finite Difference Time Domain (FDTD) algorithm can be used for acoustic wave simulation [10] and also for electromagnetic simulation [10-12]. In the case considered, it will take into account pressure waves, and will omit elastic waves. Water was chosen as the background medium. The first order acoustic equation is defined as
| (1) |
| (2) |
where:
![]() - pressure
field
- pressure
field ![]() ,
,
![]() - vector
velocity field
- vector
velocity field ![]() ,
,
![]() - mass density
of water
- mass density
of water ![]() ,
,
![]() - relative to
- relative to ![]() mass density of the medium,
mass density of the medium,
![]() - velocity of sound.
- velocity of sound.
Gradient is defined by
| (3) |
Divergence in Cartesian coordinates is
| (4) |
It can be defined compressibility ![]()
![]() as
as
| (5) |
After simple calculations, the equation (1) can be written as
| (6) |
After first-order differencing in space and time, the equation above can be written as
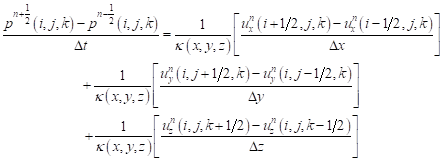 | (7) |
After subsequent conversions, it was obtained
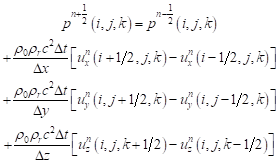 | (8) |
Similar calculations of Eq. (2) allowed one to receive
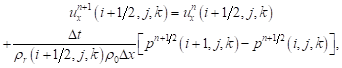 | (9) |
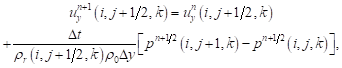 | (10) |
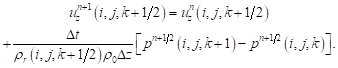 | (11) |
Simplified to a one-dimensional case, it was obtained
| (12) |
| (13) |
where
| (14) |
| (15) |
The Courant equation determined the ![]() and
and ![]() parameters
parameters
| (16) |
![]() is the fastest
velocity of sound in the simulation.
is the fastest
velocity of sound in the simulation.
1.2. Discrete Fourier Transform
All implementation used in the paper was made
in the Wolfram Language in Mathematica. The definition of discrete Fourier
transform ![]() of a list
of a list ![]() of
length
of
length ![]() is described by the equation
is described by the equation
| (17) |
The power spectrum is defined by
| (18) |
and the results are normalized in frequency domain.
1.3. Transfer Matrix Method algorithm
The Transfer Matrix Method (TMM) algorithm can be used to analyze 1D phononic crystal transmission properties for acoustic/elastic waves. The equation (19) describes the pressure of the acoustic wave which is propagating in a multilayer medium from left to right.
| (19) |
Where ![]() is
the acoustic wave phase velocity and the corresponding layer is described by
subscript
is
the acoustic wave phase velocity and the corresponding layer is described by
subscript ![]() . The solution of one-dimensional plane
wave takes the form
. The solution of one-dimensional plane
wave takes the form
| (20) |
The first term on the right side of equation
(20) is the transmitted wave and
the second is reflected one. The ![]() is frequency in the
wave number described as
is frequency in the
wave number described as ![]() .
.
The transmission coefficient is defined as
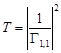 | (21) |
where ![]() is the
characteristic matrix for the multilayer structure described by
is the
characteristic matrix for the multilayer structure described by
| (22) |
![]() is the matrix which
describes the interfaces between the layers and is
defined as
is the matrix which
describes the interfaces between the layers and is
defined as
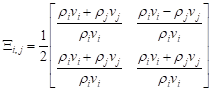 | (23) |
In the equation above, ![]() is mass density of layer
is mass density of layer ![]() . Propagation in layer
. Propagation in layer ![]() is defined by the matrix
is defined by the matrix
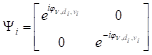 | (24) |
The ![]() function
takes the form
function
takes the form
| (25) |
where ![]() is the thickness of
layer
is the thickness of
layer ![]() .
.
1.4. Severin superlattice
Using the recursive rule of substitution, the
aperiodic Severin structure ![]() [13] can be obtained
[13] can be obtained
| (26) |
![]() is the initial
condition. The generations where L is respectively equal to 3, 4 and 5 in the
Severin superlattice are described by the formula (26) and listed in Table 1.
Initial structural values are defined as:
is the initial
condition. The generations where L is respectively equal to 3, 4 and 5 in the
Severin superlattice are described by the formula (26) and listed in Table 1.
Initial structural values are defined as:
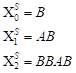 | (27) |
Table 1
Arrangement of the layers structure for L generations of the Severin superlattices
|
|
|
|
3 |
ABABBBAB |
|
4 |
BBABBBABABABBBAB |
|
5 |
ABABBBABABABBBABBBABBBABABABBBAB |
2. Implementation
2.1. TMM initialization
The listing below shows the variable initialization. The lx describes the superlattice structure made from A and B materials types with initial values of properties v1, ro1 and d1. Where v1 is phase velocity of the medium, ro1 is mass density and d1 is thickness of the layer.

The listing below corresponds to equations (21), (22), (23), (24) and (25). The T function returns the transmission coefficient for a given structure and frequency.

2.2. Implementation of FDTD
The sev* variables describes aperiodic Severin superlattice structures which are given in Table 1. In param are the properties of surrounding medium and properties of used materials. The cmax parameter is the maximum velocity in the simulation which is needed to calculate dt from the Courant condition. The freqIn is a frequency and npml is number of PML boundary conditions. The grA and grB are thickness of layers A and B respectively. After that, there are the roStruct and cStruct functions which initialize the material constants of the studied structure. The first two sub-lists in the parameter param define the symbol of the input in and output out material. The structure of the remaining sub-lists is constructed in the following way: the first element is the symbol of a given material, the second is the material density [kg/m3], the third is phase velocity [m/s], and the last is the material name.



In the For loop below, the PML boundary conditions are initialized.

Main loop alternately calculates equations (12) and (13). As can be seen, pulse is soft sinusoidal source with freqIn frequency.

According to Equations (17) and (18), the Discrete Fourier Transform and the power spectrum are designated by
3. Research
In this paper, the properties of aperiodic Severin superlattices were analyzed. Input and output medium was material A which was water with a mass density of 1000 kg/m3 and a phase velocity of 1500 m/s; B material was steel with parameters respectively 7800 kg/m3 and 5900 m/s. Thickness of the single layer A or B was equal 0.1 m. Figure 1 shows TMM results for Severin aperiodic superlattice with generation number L equal to 3, 4 or 5. By analyzing the results, it can be seen that as the complexity of the structure increases and the number of transmission bands increases as well. An interesting result can be observed for frequency f0 on Figure 1d, where L = 3 there is almost no acoustic wave transmission, then for L = 4 there is a transmission peak equal to half of the maximal value, and for L = 5 the peak doubles its intensity.
After passing through the multilayer structure, after multiple reflections within the composite, the superposition of acoustic waves occurs in the output. The output signal can be analyzed using the Discrete Fourier Transforms. Figure 2 shows the power spectrum after t steps of FDTD simulation for each considered L generation of the Severin multilayer. Source frequency was set to 734.88 Hz. As shown in Figure 2, the output signal at the frequency domain shows the presence of peaks. For an 8-layered structure of L = 3 generation (Fig. 2a) there are observed in frequency domain in 3.69 kHz and 3.81 kHz. Below 3 kHz for L equal to 3 and 4 there are no peaks observed. After doubling the complexity of the Severin structure (L = 4, Fig. 2b) maximum function values occurs at 3.69, 3.76 and 3.8 kHz.
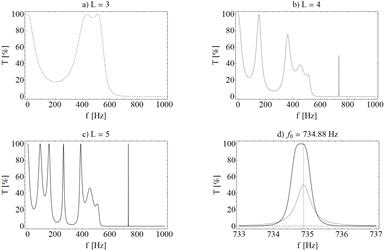
Fig. 1. Transmission maps of Severin superlattices calculated by the TMM algorithm for L generations respectively a) L = 3, b) L = 4, c) L = 5, d) transmission values for f0 frequency are collected in Table 2
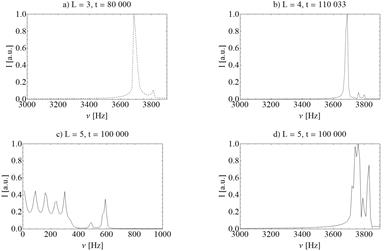
Fig. 2. Power spectrum of Severin superlattices calculated by FDTD with DFT algorithm for source frequency f0 = 734.88 Hz; a) L = 3, b) L = 4, c) L = 5, frequency range up to 1 kHz, d) L = 5, frequency range from 3 to 3.9 kHz
Table 2
Transmission values for generation number L in f0 = 734.88 Hz
|
L |
3 |
4 |
5 |
|
T |
0.24% |
50.1% |
99.35% |
A much more interesting situation occurs for L = 5 (Fig. 2c) where there are components with frequencies below 650 Hz with maxima of 90, 160, 240, 300, 490, 590 Hz. In the range of 3.6¸3.9 kHz, maximum frequencies occur at 3.72, 3.74, 3.76, 3.79 and 3.83 kHz.
4. Conclusions
The transmission properties of the aperiodic filters structure obtained using the TMM algorithm are very important for many types of acoustic devices such as selective filters, wave guides, noise control or demultiplexing. The output signal properties can by studied by FDTD with DFT.
In the paper, transmission properties of an aperiodic Severin multilayer structure was analyzed. The TMM algorithm shows the passband of the investigated filter. The most interesting was the appearance of a narrow band at f0 = 734.88 Hz which can be used as selective filter. The structure of the output signal was analyzed and for L = 5 generation of the filter appeared signal below 650 Hz.
References
[1] Gruszka K., Nabiałek M., Szota M., The influence of fill factor on the phononic crystal eigenfrequencies, Archives of Materials Science and Engineering 2014, 66(2), 74-80.
[2] Gruszka K., Nabiałek M., Szota M., Influence of rod diameter on acoustic band gaps in 2D phononic crystal, Archives of Materials Science and Engineering 2014, 68(1), 24-30.
[3] Qiu C.Y., Liu Z.Y., Jun Z.M., Shi J., Mode-selecting acoustic filter by using resonant tunneling of two-dimensional double phononic crystals, Applied Physics Letters 2005, 87, 104101.
[4] Cicek A., Kaya O.A., Yilmaz M., Ulug B., Slow sound propagation in a sonic crystal linear waveguide, Journal of Applied Physics 2012, 111, 013522.
[5] Zhang M.D., Zhong W., Zhang X.D., Defect-free localized modes and coupled-resonator acoustic waveguides constructed in two-dimensional phononic quasicrystals, Journal of Applied Physics 2012, 111, 104314.
[6] Sánchez-Dehesa J., Garcia-Chocano V.M., Torrent D., Cervera F., Cabrera S., Noise control by sonic crystal barriers made of recycled materials, The Journal of the Acoustical Society of America 2011, 129, 1173.
[7] Wu T.T., Wu L.C., Huang Z.G., Frequency band-gap measurement of two-dimensional air/silicon phononic crystals using layered slanted finger interdigital transducers, Journal of Applied Physics 2005, 97, 094916.
[8] Pennec Y., Djafari-Rouhani B., Vasseur J.O., Khelif A., Deymier P.A., Tunable filtering and demultiplexing in phononic crystals with hollow cylinders, Physical Review E - Statistical, Nonlinear, and Soft Matter Physics 2004, 69, 046608.
[9] Olsson R.H., El-Kady I., Microfabricated phononic crystal devices and applications, Measurement Science and Technology 2009, 20, 012002.
[10] Sullivan D.M., Electromagnetic Simulation Using the FDTD Method, IEEE Press, New York 2000.
[11] Garus S., Garus J., Szlązak K., Nabiałek M., Pietrusiewicz P., Błoch K., Gruszka K., Szota M., The influence of extinction coefficient on transmission in binary multilayer, Journal of Achievements in Materials and Manufacturing Engineering 2013, 61/2, 236-243.
[12] Garus S., Garus J., Szota M., Nabiałek M., Gruszka K., Błoch K., Transmission in combination of structures, Archives of Materials Science and Engineering 2013, 64/2, 110-117.
[13] Severin M., Dulea M., Riklund R., Periodic and quasiperiodic wavefunctions in a class of one dimensional quasicrystals: an analytical treatment, Journal of Physics: Condensed Matter 1989, 1, 8851.


