Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method
Gbeminiyi Sobamowo
,Lawrence Jayesimi
,James Femi-Oyetoro
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Sobamowo_2017,
doi = {10.17512/jamcm.2017.3.08},
url = {https://doi.org/10.17512/jamcm.2017.3.08},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {3},
pages = {85--96},
author = {Gbeminiyi Sobamowo and Lawrence Jayesimi and James Femi-Oyetoro},
title = {Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.3.08 UR - https://doi.org/10.17512/jamcm.2017.3.08 TI - Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Sobamowo, Gbeminiyi AU - Jayesimi, Lawrence AU - Femi-Oyetoro, James PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 85 EP - 96 IS - 3 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Sobamowo, G., Jayesimi, L., & Femi-Oyetoro, J. (2017). Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method. Journal of Applied Mathematics and Computational Mechanics, 16(3), 85-96. doi:10.17512/jamcm.2017.3.08
Sobamowo, G., Jayesimi, L. & Femi-Oyetoro, J., 2017. Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method. Journal of Applied Mathematics and Computational Mechanics, 16(3), pp.85-96. Available at: https://doi.org/10.17512/jamcm.2017.3.08
[1]G. Sobamowo, L. Jayesimi and J. Femi-Oyetoro, "Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 3, pp. 85-96, 2017.
Sobamowo, Gbeminiyi, Lawrence Jayesimi, and James Femi-Oyetoro. "Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method." Journal of Applied Mathematics and Computational Mechanics 16.3 (2017): 85-96. CrossRef. Web.
1. Sobamowo G, Jayesimi L, Femi-Oyetoro J. Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(3):85-96. Available from: https://doi.org/10.17512/jamcm.2017.3.08
Sobamowo, Gbeminiyi, Lawrence Jayesimi, and James Femi-Oyetoro. "Heat transfer study in a convective-radiative fin with temperature-dependent thermal conductivity and magnetic field using variation parameters method." Journal of Applied Mathematics and Computational Mechanics 16, no. 3 (2017): 85-96. doi:10.17512/jamcm.2017.3.08
HEAT TRANSFER STUDY IN A CONVECTIVE-RADIATIVE FIN WITH TEMPERATURE-DEPENDENT THERMAL CONDUCTIVITY AND MAGNETIC FIELD USING VARIATION PARAMETERS METHOD
Gbeminiyi Sobamowo1, Lawrence Jayesimi2, James Femi-Oyetoro3
1Department of Mechanical Engineering,
University of Lagos
2Works and Physical Planning Department, University of Lagos
Akoka, Lagos, Nigeria
3Department of Mechanical Engineering, University of Ibadan
Oyo, Nigeria
mikegbeminiyi@gmail.com, lawrenceunilag@yahoo.com, jamesfemioyetoro@gmail.com
Received: 25 February 2017; Accepted: 25 July 2017
Abstract. In this work, a heat transfer study is carried out in a convective-radiative straight fin with temperature-dependent thermal conductivity and a magnetic field using the variation of parameters method. The developed heat transfer model is used to analyze the thermal performance, establish the optimum thermal design parameters and investigate the effects of thermo-geometric parameters and non-linear thermal conductivity parameters on the thermal performance of the fin. The results obtained are compared with the results in literature and good agreements are found. The analysis can serve as basis for comparison of any other method of analysis of the problem and it also provides a platform for improvement in the design of fin in heat transfer equipment.
MSC 2010: 35A15
Keywords: heat transfer study, convective-radiative fin, variation of parameters method, temperature-dependent thermal conductivity and magnetic field
1. Introduction
The study of heat transfer enhancement in thermal components and devices has been a subject of interest for many years. The nonlinearities in the developed thermal model of the passive devices such as fins and spines for the cooling of thermal systems have attracted a large number of research works. In fact, in the past few decades, different solutions to the nonlinear equations have been developed using different techniques. Aziz and Enamul-Huq [1] applied regular perturbation expansion to study a pure convection fin with temperature dependent thermal conductivity. Aziz [2] extended the previous analysis to include a uniform internal heat generation in the fin. A few years later, Campo and Spaulding [3] applied the method of successive approximation to predict the thermal behaviour of uniform circumferential fins. Chiu and Chen [4] and Arslanturk [5] adopted the Adomian decomposition Method (ADM) to obtain the temperature distribution in a pure convection fin with variable thermal conductivity. The same problem was also solved by Ganji [6] with the aid of the homotopy perturbation method originally proposed by He [7]. Chowdhury and Hashim [8] applied the Adomian decomposition method to evaluate the temperature distribution of the straight rectangular fin with temperature dependent surface flux for all possible types of heat transfer. In the following year, Rajabi [9] employed the homotopy perturbation method (HPM) to calculate the efficiency of straight fins with temperature-dependent thermal conductivity. A year later, Mustapha [10] adopted the homotopy analysis method (HAM) to find the efficiency of straight fins with temperature-dependent thermal conductivity. Also, Coskun and Atay [11] utilized the variational iteration method (VIM) for the analysis of convective straight and radial fins with temperature- -dependent thermal conductivity while Languri et al. [12] applied both variation iteration and homotopy perturbation methods for the evaluation of efficiency of straight fins with temperature-dependent thermal conductivity. Coskun and Atay [13] applied the variational iteration method to analyze the efficiency of convective straight fins with temperature-dependent thermal conductivity. In the same year, Atay and Coskum [14] employed the variation iteration and finite element methods to carry out a comparative analysis of power-law-fin type problems. Domairry and Fazeli [15] used the homotopy analysis method to determine the efficiency of straight fins with temperature-dependent thermal conductivity. Hosseini et al. [16] applied the homotopy analysis method to provide approximate but accurate solution of heat transfer in a fin with temperature-dependent internal heat generation and thermal conductivity. Joneidi et al. [17], Moradi and Ahmadikia [18] Moradi [19], Mosayebidorcheh et al. [20], Ghasemi et al. [21], Sandri et al. [22], Ganji and Dogonchi [23] presented analytical solution for a fin with temperature dependent thermal coefficient using the differential transform method (DTM). Method of weighted residual are applied by Lederi et al. [24] and Sobamowo [25] to the problem.
Variation parameter method (VPM) is an approximate analytical method which has been applied to solve different linear and nonlinear differential equations [21-25]. It is different from variational iteration method (VIM) in many aspects. In VIM, the multiplier used called Lagrange Multiplier can be of different forms. Exact, semi-exact and approximate multipliers are used for the purposed. However, in VPM, there is no concept of exact and approximate multipliers. The multiplier used in VPM is calculated by Wronskian technique. Also, VIM takes into account the complete equation for the solution purposes while VPM gives the solution of the problem without taking highest order term into consideration [26]. Its main advantages is in its ability to solves nonlinear differential and integral equations without linearization, discretization, restrictive assumptions, perturbation, approximations, round-off error, Adomian polynomial and conformity of the solution to the rule of coefficient ergodicity. Moreover, the solutions by most of the previous approximate analytical methods come with large number of terms which are not convenient for use by designers and engineers [27]. However, the solutions of VPM are comparative concise and the results are completely reliable and physically realistic. To the best of the authors’ knowledge, the analysis of heat transfer in a convective-radiative fin subjected to a temperature-dependent thermal conductivity and magnetic field using variation parameter method has not been carried out. Therefore, in this present study, the variation parameters method (VPM) is used to develop approximate analytical solutions for heat transfer in convective-radiative fin with temperature-dependent thermal conductivity and magnetic field. The developed symbolic thermal models were used to investigate the effects of convective, radiative, magnetic parameters on the thermal performance of the fin. The analytical solutions as developed in this work, can serve as a starting point for a better understanding of the relationship between the physical quantities of the problems as it provides continuous physical insight into the problem rather than pure numerical or computation methods.
2. Problem formulation
Consider a
convective-radiative straight fin of temperature-dependent thermal conductivity
k(T), length L and thickness δ that is exposed on
both faces to a convective environment at temperature ![]() and
with heat transfer co-efficient h shown in Figure 1, assuming that the heat flow in the fin and its
temperatures remain constant with time, the temperature of the medium
surrounding the fin is uniform, the fin base temperature is uniform, there is
no contact resistance where the base of the fin joins the prime surface. In
addition, fin thickness is small compared with its width and length, so
temperature gradients across the fin thickness and heat transfer from the edges
of the fin may be neglected. The
dimension x pertains to the length coordinate which has its origin at
the tip of the fin and has a positive orientation from the fin tip to the fin
base. Following the model assumptions, the governing differential equation for
the problem is shown in equation (1).
and
with heat transfer co-efficient h shown in Figure 1, assuming that the heat flow in the fin and its
temperatures remain constant with time, the temperature of the medium
surrounding the fin is uniform, the fin base temperature is uniform, there is
no contact resistance where the base of the fin joins the prime surface. In
addition, fin thickness is small compared with its width and length, so
temperature gradients across the fin thickness and heat transfer from the edges
of the fin may be neglected. The
dimension x pertains to the length coordinate which has its origin at
the tip of the fin and has a positive orientation from the fin tip to the fin
base. Following the model assumptions, the governing differential equation for
the problem is shown in equation (1).
Based on Darcy’s model and following the above assumptions, the thermal energy balance could be expressed
| (1) |
where
| (2) |
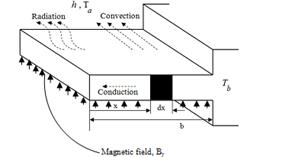
Fig. 1. Schematic of the convective-radiative longitudinal porous fin with magnetic field
As dx→0, Eq. (1) reduces
| (3) |
From Fourier’s law of heat conduction, the rate of heat conduction in the fin is given by
| (4) |
where
Following the Rosseland diffusion approximation, the radiation heat transfer rate is
| (5) |
Therefore, the total rate of heat transfer is given by
| (6) |
Substituting Eq. (6) into Eq. (3), we have
| (7) |
Further simplification of Eq. (10) gives the governing differential equation for the fin as
| (8) |
The boundary conditions are
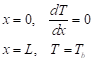 | (9) |
But
| (10) |
After substitution of Eq. (10) into Eq. (8), we arrived at
| (11) |
The case considered in this work is a situation where a small temperature difference exists within the material during the heat flow. This actually necessitated the use of temperature-invariant physical and thermal properties of the fin. Also, it has been established that under such a scenario, the term T4can be expressed as a linear function of temperature. Therefore, we have
| (12) |
Substituting Eq. (12) into Eq. (11), taking the magnetic term as linear function of temperature, we arrived at
| (13) |
| On introducing the following dimensionless parameters in Eq. (14) into Eq. (13), |
| (14) |
we arrived at the dimensionless form of the governing Eq. (13) as
| (15) |
Then
| (16) |
which is the same as
| (17) |
where
| (18) |
and the dimensionless boundary conditions
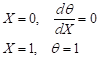 | (19) |
2. Brief introduction of variation of parameters method
The basic concept of VPM for solving differential equations is given in [28-30] as follows: Consider the general second-order boundary value problem
| (20) |
With the boundary conditions
| (21) |
The variation of the parameters method provides the general solution as
| (22) |
where: ![]() is the complementary solution of
Eq. (20),
is the complementary solution of
Eq. (20), ![]() is the function that represent the
governing equation without the highest order term.
is the function that represent the
governing equation without the highest order term.
The
particular solution is obtained by using the variation of parameters method. Replacing
the constants![]() in the complementary solution by parameters,
moving the variable inside the integral sign which was outside in Eq. (22),
imposing the boundary conditions, we have an iterative scheme of the form
in the complementary solution by parameters,
moving the variable inside the integral sign which was outside in Eq. (22),
imposing the boundary conditions, we have an iterative scheme of the form
| (23) |
h(x) is a function of x, consist of the term that arise outside the integral after using the boundary conditions in Eq. (21). Taking h(x) as initial guess, i.e., h(x) = yo(x) and g(x,s) = (x ‒ s), we have
| (24) |
4. Solution procedure using the variation of parameters method
Applying the variation of parameters method to solve Eq. (17) with the associated boundary conditions in Eq. (19), we have
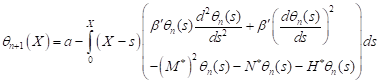 | (25) |
with n = 0,1,2,…,
here ![]() is a constant that represents the tip
dimensionless temperature.
is a constant that represents the tip
dimensionless temperature.
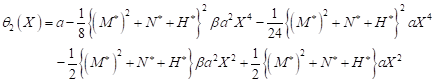 | (27) |
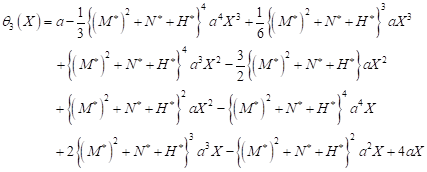 | (28) |
Following the same procedure, we can find the
other approximation for ![]() and the constant
and the constant ![]() can be determined by using the boundary
condition,
can be determined by using the boundary
condition,![]() .
.
5. Results and discussion
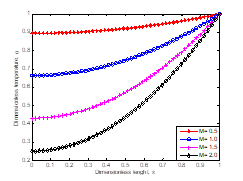
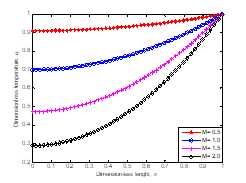
Figures 2 and 3 show the variation of dimensionless temperature with dimensionless length of the fin when the effects of radiation heat transfer and magnetic field are not included or considered. Also, the figures depict the effect of the thermogeometric parameter on the fin. From the figure, as the thermogeometric parameter increases, the rate of convective heat transfer as depicted in the Figures.
|
Fig. 2. Effects of thermogeometric parameter on the temperature distribution in the fin when β = 0.1, N = H = 0 |
Fig. 3. Effects of thermogeometric parameter on the temperature distribution in the fin when β = 0.3, N = H = 0 |
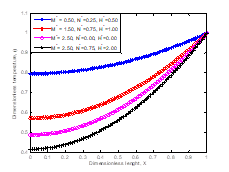
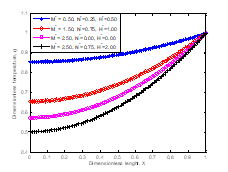
Figures 4 and 5 show the effects the thermo-geometric term, radiation number and magnetic number (Hartmann number) on the dimensionless temperature distribution or the thermal performance of the fin. Also, the figures depict the effects of the nonlinear parameter or temperature-dependent thermal conductivity term on the thermal performance of the fin. From the Figures, it could be deducted that the nonlinear thermal conductivity parameter, thermogeometric term, radiation number and magnetic number (Hartmann number) have direct and significant effects on the rate of heat transfer at the base of the fin. It shows that the rate of heat transfer increases with the radiation and Hartmann number when comparing Figures 2-5.
|
Fig. 4. Effects of radiation and Hartmann numbers on the temperature distribution in the fin when β = 0.5 |
Fig. 5. Effects of radiation and Hartmann numbers on the temperature distribution in the fin when β = 1.5 |
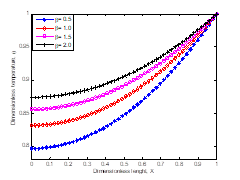
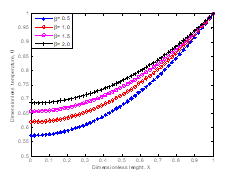
Figures 6 and 7 show the effects of non-linear thermal conductivity on the fin thermal performance under different thermogeometric parameter, radiation number and Hartmann number. The results show that performance of the fin temperature decreases with an increase in the nonlinear term or the thermal conductivity number.
|
Figs. 6. Effects of non-linear parameter on the temperature distribution in the fin when M = 0.50, N = 0.25, H = 0.50 |
Figs. 7. Effects of non-linear parameter on the temperature distribution in the fin when M = 1.50, N = 0.75, H = 1.00 |
Table 1 shows the comparison of past results in literature using other methods with the present study using the variation of the parameter method. From the table, it shows that the variation of the parameter method agree excellently with both the results of exact analytical solutions and the results of the Adomian decomposition method (ADM) and Galerkin’s method of weighted residual (GMWR) as found in literature.
Table 1
Comparison of results when β = 0.00, M = 1.00, N = 0.00, H = 0.00
|
X |
Exact |
ADM [5] |
GMWR [25] |
VPM (The present study) |
|
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 |
0.648054 0. 651297 0.661059 0. 677436 0.700594 0.730763 0.768246 0.813418 0.866731 0. 928718 1.000000 |
0.648054 0.651297 0.661059 0.677436 0.700594 0.730763 0.768246 0.813418 0.866731 0.928718 1.000000 |
0.648054 0.651297 0.661059 0.677436 0.700594 0.730763 0.768246 0.813418 0.866730 0.928718 1.000000 |
0.648054 0.651297 0.661057 0.677436 0.700594 0.730763 0.768246 0.813418 0.866731 0.928718 1.000000 |
6. Conclusion
In this work, heat transfer study in a convective-radiative straight fin with temperature-dependent thermal conductivity and magnetic field has been carried out using the variation of parameters method. The developed heat transfer model was used to analyze the thermal performance, establish the optimum thermal design parameters and investigate the effects of thermogeometric parameters and thermal conductivity (non-linear) parameters on the thermal performance of the fin. The results obtained were compared with the results in literature and good agreements were found. The analysis can serve as a basis for comparison of any other method of analysis of the problem, and they also provide platform for improvement in the design of fin in heat transfer equipment.
Nomenclature
|
L Ac Ap h H k ka
M m2 N P |
length of the fin cross sectional area of the fins profile area of the fins heat transfer coefficient Hartmann number thermal conductivity of the fin material thermal conductivity of the fin material at ambient temperature dimensionless thermogeometric fin parameter thermogeometric fin parameter dimensionless radiation number perimeter of the fin |
T Ta Tb x X
β
δ θ ε σ |
temperature ambient temperature temperature at the base of the fin fin axial distance [m] dimensionless length of the fin Greek symbols thermal conductivity parameter or non- linear parameter thickness of the fin [m] dimensionless temperature emmisivity of the fin Stefan-Boltzmann constant |
References
[1] Aziz A., Enamul-Huq S.M., Perturbation solution for convecting fin with temperature dependent thermal conductivity, J. Heat Transfer 1973, 97, 300-301.
[2] Aziz A., Perturbation solution for convecting fin with internal heat generation and temperature dependent thermal conductivity, Int. J. Heat Mass Transfer 1977, 20, 1253-5.
[3] Campo A., Spaulding R.J., Coupling of the methods of successive approximations and undetermined coefficients for the prediction of the thermal behaviour of uniform circumferential fins, Heat and Mass Transfer 1999, 34, 6, 461-468.
[4] Ching-Huang Chiu, Cha’o-Kuang Chen, A decomposition method for solving the convectice longitudinal fins with variable thermal conductivity, Int. J. Heat and Mass Transfer 2002, 45, 2067-2075.
[5] Arslanturk A., A decomposition method for fin efficiency of convective straight fin with temperature dependent thermal conductivity, Int. Commun. Heat Mass Transfer 2005, 32, 831-841.
[6] Ganji D.D., The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer, Phys. Lett. 2006, A355, 337-341.
[7] He J.H., Homotopy perturbation method, Comp. Methods Appl. Mech. Eng. 1999, 178, 257-262.
[8] Chowdhury M.S.H., Hashim I., Analytical solutions to heat transfer equations by homotopy-perturbation method revisited, Physical Letters 2008, A372, 1240-1243.
[9] Rajabi A., Homotopy perturbation method for fin efficiency of convective straight fins with temperature dependent thermal conductivity, Physics Letters 2007, A364, 33-37.
[10] Mustafa Inc, Application of homotopy analysis method for fin efficiency of convective straight fin with temperature dependent thermal conductivity, Mathematics and Computers Simulation 2008, 79, 189-200.
[11] Coskun S.B., Atay M.T., Analysis of convective straight and radial fins with temperature dependent thermal conductivity using variational iteration method with comparision with respect to finite element analysis, Mathematical Problem in Engineering, vol. 2007, Article ID 42072.
[12] Languri E.M., Ganji D.D., Jamshidi N., Variational iteration and homotopy perturbation methods for fin efficiency of convective straight fins with temperature dependent thermal conductivity, 5th WSEAS Int. Conf. on Fluid Mechanics (fluids 08), Acapulco, Mexico 2008, January 25-27.
[13] Coskun S.B., Atay M.T., Fin efficiency analysis of convective straight fin with temperature dependent thermal conductivity using variational iteration method, Appl. Therm. Eng. 2008, 28, 2345-2352.
[14] Atay M.T., Coskun S.B., Comparative analysis of power-law fin-type problems using variational iteration method and finite element method, Mathematical Problems in Engineering 2008, Article ID 635231.
[15] Domairry G., Fazeli M., Homotopy analysis method to determine the fin efficiency of convective straight fins with temperature dependent thermal conductivity, Communication in Nonlinear Science and Numerical Simulation 2009, 14, 489-499.
[16] Hosseini K., Daneshian B., Amanifard N., Ansari R., Homotopy analysis method for a fin with temperature dependent internal heat generation and thermal conductivity, International Journal of Nonlinear Science 2012, 14, 2, 201-210.
[17] Joneidi A.A., Ganji D.D., Babaelahi M., Differential Transformation Method to determine fin efficiency of convective straight fins with temperature dependent thermal conductivity, International Communication in Heat and Mass Transfer 2009, 36, 757-762.
[18] Moradi A., Ahmadikia H., Analytical solution for different profiles of fin with temperature dependent thermal conductivity, Hindawi Publishing Corporation Mathematical Problem in Engineering, vol. 2010, Article ID 568263, 15.
[19] Moradi A., Ahmadikia H., Investigation of effect thermal conductivity on straight fin performance with DTM, International Journal of Engineering and Applied Sciences (IJEAS) 2011, 1, 42-54.
[20] Mosayebidorcheh S., Ganji D.D., Masoud Farzinpoor, Approximate solution of the nonlinear heat transfer equation of a fin with the power-law temperature-dependent thermal conductivity and heat transfer coefficient, Propulsion and Power Reasearch 2014, 41-47.
[21] Ghasemi S.E., Hatami M., Ganji D.D., Thermal analysis of convective fin with temperature-dependent thermal conductivity and heat generation, Cases Studies in Thermal Engineering 2014, 4, 1-8.
[22] Sadri S., Raveshi M.R., Amiri S., Efficiency analysis of straight fin with variable heat transfer coefficient and thermal conductivity, Journal of Mechanical Science and Technology 2012, 26, 4, 1283-1290.
[23] Ganji D.D., Dogonchi A.S., Analytical investigation of convective heat transfer of a longitudinal fin with temperature-dependent thermal conductivity, heat transfer coefficient and heat generation, International Journal of Physical Sciences 2014, 9(21), 466-474.
[24] Ledari S.T., Mirgolbabaee H., Ganji D.D., Heat transfer analysis of a fin with temperature dependent thermal conductivity and heat transfer coefficient, NTMSCI 2015, 3(2), 55-69.
[25] Sobamowo M.G., Thermal analysis of longitudinal fin with temperature-dependent properties and internal heat generation using Galerkin’s method of weighted residual, Applied Thermal Engineering 2016, 99, 1316-1330.
[26] Fernandez A., On some approximate methods for nonlinear models, Appl. Math. Comput. 2009, 215, 168-174.
[27] Aziz A., Bouaziz M.N., A least squares method for a longitudinal fin with temperature dependent internal heat generation and thermal conductivity, Energy Conversion and Management 2011, 52, 2876-2882.
[28] Mohyud-din S.T., Noor M.A., Waheed A., Variation of parameters method for solving sixth-order boundary value problems commun, Korean Math. Soc. 2009, 24, 4, 605-615.
[29] Mohyud-Din S.T., Noor M.A., Noor K.I., Modified variation of parameters method for solving partial differential equations, Int. J. Mod. Phys. 2009, B.
[30] Mohyud-Din S.T., Noor M.A., Noor K.I., Waheed A., Modified variation of parameters method for solving nonlinear boundary value problems, Int. J. Mod. Phys. 2009, B.


