Properties of entire solutions of some linear PDE's
Andriy Bandura
,Oleh Skaskiv
,Petro Filevych
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Bandura_2017,
doi = {10.17512/jamcm.2017.2.02},
url = {https://doi.org/10.17512/jamcm.2017.2.02},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {2},
pages = {17--28},
author = {Andriy Bandura and Oleh Skaskiv and Petro Filevych},
title = {Properties of entire solutions of some linear PDE's},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.2.02 UR - https://doi.org/10.17512/jamcm.2017.2.02 TI - Properties of entire solutions of some linear PDE's T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Bandura, Andriy AU - Skaskiv, Oleh AU - Filevych, Petro PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 17 EP - 28 IS - 2 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Bandura, A., Skaskiv, O., & Filevych, P. (2017). Properties of entire solutions of some linear PDE's. Journal of Applied Mathematics and Computational Mechanics, 16(2), 17-28. doi:10.17512/jamcm.2017.2.02
Bandura, A., Skaskiv, O. & Filevych, P., 2017. Properties of entire solutions of some linear PDE's. Journal of Applied Mathematics and Computational Mechanics, 16(2), pp.17-28. Available at: https://doi.org/10.17512/jamcm.2017.2.02
[1]A. Bandura, O. Skaskiv and P. Filevych, "Properties of entire solutions of some linear PDE's," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 2, pp. 17-28, 2017.
Bandura, Andriy, Oleh Skaskiv, and Petro Filevych. "Properties of entire solutions of some linear PDE's." Journal of Applied Mathematics and Computational Mechanics 16.2 (2017): 17-28. CrossRef. Web.
1. Bandura A, Skaskiv O, Filevych P. Properties of entire solutions of some linear PDE's. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(2):17-28. Available from: https://doi.org/10.17512/jamcm.2017.2.02
Bandura, Andriy, Oleh Skaskiv, and Petro Filevych. "Properties of entire solutions of some linear PDE's." Journal of Applied Mathematics and Computational Mechanics 16, no. 2 (2017): 17-28. doi:10.17512/jamcm.2017.2.02
PROPERTIES OF ENTIRE SOLUTIONS OF SOME LINEAR PDE'S
Andriy Bandura1, Oleh Skaskiv2, Petro Filevych3
1Department
of Advanced Mathematics, Ivano-Frankivsk National
Technical University of Oil
and Gas, Ivano-Frankivsk, Ukraine
2Department of Function Theory and Theory of Probability, Ivan
Franko National University of Lviv Lviv, Ukraine
3Department of Information Technologies, Vasyl Stephanyk
Precarpathional National University Ivano-Frankivsk, Ukraine
andriykopanytsia@gmail.com, olskask@gmail.com, filevych@mail.ru
Received: 22 April 2017; accepted: 15 May 2017
Abstract. In
this paper, there are improved sufficient conditions of boundedness of the
![]() -index in a direction for entire
solutions of some linear partial differential equations. They are new even for
the one-dimensional case and
-index in a direction for entire
solutions of some linear partial differential equations. They are new even for
the one-dimensional case and ![]() Also, we found a
positive continuous function
Also, we found a
positive continuous function ![]() such that entire
solutions of the homogeneous linear differential equation with arbitrary fast
growth have a bounded
such that entire
solutions of the homogeneous linear differential equation with arbitrary fast
growth have a bounded ![]() -index and estimated its
growth.
-index and estimated its
growth.
MSC 2010: 34M05, 34M10, 35B08, 35B40, 32A15, 32A17
Keywords: linear partial
differential equation, entire function, bounded ![]() -index
in direction, bounded
-index
in direction, bounded ![]() -index, homogeneous linear
differential equation, growth of solutions
-index, homogeneous linear
differential equation, growth of solutions
1. Introduction
Let ![]() be a continuous function. An entire function
be a continuous function. An entire function ![]() ,
, ![]() , is
called [1-4] a function of
bounded
, is
called [1-4] a function of
bounded ![]() -index in a direction
-index in a direction ![]() , if there exists
, if there exists ![]() such that
such that
![]() (1)
(1)
for every ![]() and
every
and
every ![]() , where
, where ![]()
![]()
![]()
![]() The
least such integer
The
least such integer ![]() is called the
is called the ![]() -index in the direction
-index in the direction ![]() of the entire function
of the entire function ![]() and is denoted by
and is denoted by ![]() In the case
In the case ![]()
![]()
![]()
![]() we
obtain the definition of an entire function of one
variable of bounded
we
obtain the definition of an entire function of one
variable of bounded ![]() -index (see [5,
6]). And the value of the
-index (see [5,
6]). And the value of the ![]() -index
is denoted by
-index
is denoted by ![]()
This paper is devoted to three problems in
theory of partial differential equations in ![]() and
differential equations in a complex plane.
and
differential equations in a complex plane.
At first, we consider the partial differential equation
| (2) |
where ![]()
![]() are entire functions in
are entire functions in
![]()
![]() There
are known sufficient conditions [1, 2, 4] of boundedness of the
There
are known sufficient conditions [1, 2, 4] of boundedness of the
![]() -index in the
direction for entire solutions of (2). In particular, some inequalities must be
satisfied outside discs of any radius. Replacing the
universal quantifier by the existential, we relax the
conditions.
-index in the
direction for entire solutions of (2). In particular, some inequalities must be
satisfied outside discs of any radius. Replacing the
universal quantifier by the existential, we relax the
conditions.
Also the ordinary differential equation
| (3) |
is considered. Shah, Fricke,
Sheremeta, Kuzyk [6-8] did not
investigate an index boundedness of the entire solution
of (3) because the right hand side of (3)
is a function of two variables. But now in view of entire function theory
of bounded ![]() -index in direction,
it is natural to pose and to consider the following
question.
-index in direction,
it is natural to pose and to consider the following
question.
Problem 1 [3,
Problem 4]. Let ![]()
![]() be
a function of bounded
be
a function of bounded
![]() -index in directions
-index in directions ![]() and
and ![]() What
is a function
What
is a function ![]() such that an entire solution
such that an entire solution ![]() of equation (3) has a bounded
of equation (3) has a bounded ![]() -index?
-index?
Finally, we consider the linear homogeneous differential equation of the form
| (4) |
which is obtained from (2), if ![]()
![]()
![]()
![]() There is
a known result of Kuzyk and Sheremeta [5] about the growth of the entire
function of the bounded
There is
a known result of Kuzyk and Sheremeta [5] about the growth of the entire
function of the bounded ![]() -index. Later Kuzyk, Sheremeta [6] and Bordulyak [9] investigated the
boundedness of the
-index. Later Kuzyk, Sheremeta [6] and Bordulyak [9] investigated the
boundedness of the ![]() -index of entire solutions of equation
(4) and its growth.
-index of entire solutions of equation
(4) and its growth.
Meanwhile, many mathematicians such as
Kinnunen, Heittokangas, Korhonen, Rättya, Cao, Chen, Yang, Hamani,
Belaїdi [10-14] used the
iterated orders to study the growth of solutions (4). Lin, Tu and Shi [15] proposed a more flexible scale to study the growth of solutions. They
used ![]() -order. But, the
iterated orders and
-order. But, the
iterated orders and ![]() -orders
do not cover arbitrary growth (see example in [16]). There is considered a more general
approach to describe the relations between the growth of entire coefficients
and entire solutions of (4). In view of results from [16], the authors raise the question: what is a positive continuous function
-orders
do not cover arbitrary growth (see example in [16]). There is considered a more general
approach to describe the relations between the growth of entire coefficients
and entire solutions of (4). In view of results from [16], the authors raise the question: what is a positive continuous function ![]() such
that entire solutions of (4) with arbitrary fast growth have bounded
such
that entire solutions of (4) with arbitrary fast growth have bounded ![]() -index? We provide an answer to the question.
-index? We provide an answer to the question.
2. Auxiliary propositions and notations
For ![]()
![]()
![]() and
positive continuous function
and
positive continuous function ![]() we define
we define ![]()
![]() By
By ![]() we
denote a class of functions
we
denote a class of functions ![]() which
satisfiy the condtion
which
satisfiy the condtion ![]()
For simplicity, we also
use a notation ![]() .
.
Theorem A [1, 4]. Let ![]() An entire in
An entire in ![]() function
function ![]() is
of bounded
is
of bounded
![]() -index in direction
-index in direction ![]() if and only if there exist numbers
if and only if there exist numbers ![]() and
and ![]() ,
, ![]() and
and ![]() such
that for all
such
that for all ![]()
Let us to write ![]()
![]() ,
, ![]() - zeros of the function
- zeros of the function ![]() for a given
for a given ![]() If
for all
If
for all ![]()
![]() then
we put
then
we put ![]()
Theorem B [1,
4]. Let ![]() be an entire function of the bounded
be an entire function of the bounded ![]() -index in the
direction
-index in the
direction ![]()
![]() Then
for every
Then
for every ![]() and for every
and for every ![]() there
exists
there
exists ![]() such that for all
such that for all ![]()
![]() .
.
Theorem C [1,
4]. Let ![]() be an entire function in
be an entire function in ![]()
![]() Then
the function
Then
the function ![]() is of bounded
is of bounded ![]() -index
in the direction
-index
in the direction ![]() if and only if the following
conditions hold: 1) for every
if and only if the following
conditions hold: 1) for every ![]() there exists
there exists ![]() such
that for each
such
that for each ![]()
![]() 2) for every
2) for every ![]() there exists
there exists ![]() such that for every
such that for every ![]()
![]()
Theorem D [1,
4]. Let ![]() . An entire function
. An entire function ![]() has a
bounded
has a
bounded
![]() -index in direction
-index in direction ![]() if and only if there exist
if and only if there exist ![]() and
and ![]() such
that
such
that ![]() for each
for each ![]() .
.
Theorem E [17]. Let ![]() be a bounded closed domain in
be a bounded closed domain in ![]()
![]() be
a continuous function,
be
a continuous function, ![]() be an entire
function. Then there exists
be an entire
function. Then there exists ![]() such that for all
such that for all ![]() and for all
and for all ![]()
Theorem F [5]. Let ![]() be a positive continuously
differentiable function
of real
be a positive continuously
differentiable function
of real ![]() Suppose that
Suppose that ![]() as
as
![]() where
where ![]() If
an entire function
If
an entire function ![]() has a
bounded
has a
bounded ![]() -index then
-index then ![]()
3. Boundedness of L-index in direction of entire solutions of some linear partial differential equations
Denote ![]()
![]()
![]()
![]() where
where ![]() is a zero set of the function
is a zero set of the function
![]() The following theorem is valid.
The following theorem is valid.
Theorem 1. Let
![]() , and
, and ![]() be entire
functions of the bounded
be entire
functions of the bounded ![]() -index
in the direction
-index
in the direction ![]() Suppose that there exist
Suppose that there exist ![]() and
and ![]() such
that for each
such
that for each ![]() and
and ![]()
| (5) |
Then an entire
function ![]() satisfying (2) has bounded
satisfying (2) has bounded ![]() -index
in the direction
-index
in the direction ![]()
Proof: Theorem C provides that ![]() and
and ![]() Denote
Denote ![]() Suppose
that
Suppose
that ![]() Theorem B and
inequality (5) imply that there exist
Theorem B and
inequality (5) imply that there exist ![]() and
and ![]() such that for all
such that for all ![]()
By equation (2), we evaluate the derivative in the direction ![]()
The obtained equality implies that for all ![]() :
:
![]() Thus, there exists
Thus, there exists ![]() such that for all
such that for all ![]()
| (6) |
If ![]() then there exists a sequence of points
then there exists a sequence of points ![]() satisfying
(6) and such that
satisfying
(6) and such that ![]() with as
with as ![]() Substituting
Substituting ![]() in
(6) and taking the limit as
in
(6) and taking the limit as ![]() we obtain that this
inequality is valid for all
we obtain that this
inequality is valid for all ![]() If
If ![]() (i.e. all zeros of
(i.e. all zeros of ![]() belong to
belong to ![]() )
then by Theorem D the entire
function satisfying (2) has a bounded
)
then by Theorem D the entire
function satisfying (2) has a bounded ![]() -index in the direction
-index in the direction ![]() Otherwise,
Otherwise, ![]() . Since
. Since ![]() and
and ![]() then there exists
then there exists ![]() such that
such that ![]() Let
Let
![]() be an arbitrary point from
be an arbitrary point from ![]() and
and ![]() Since
the entire functions
Since
the entire functions ![]() have
a bounded
have
a bounded ![]() -index in the
direction
-index in the
direction ![]() by Theorem C the set
by Theorem C the set ![]() contains at most
contains at most ![]() zeros of the functions or
zeros of the functions or ![]() Let
Let ![]() be
zeros of the slice function
be
zeros of the slice function ![]() (i.e.
(i.e. ![]() ) such that
) such that ![]() where
where
![]()
![]() Since
Since
![]() we have
we have ![]() Obviously,
Obviously,
Thus, if ![]() then
(6) holds. Hence, for these points
then
(6) holds. Hence, for these points ![]() the inequality
the inequality ![]() and (6) imply
and (6) imply
| (8) |
where ![]() and
and
![]()
Let ![]() be
the sum of the diameters of
be
the sum of the diameters of ![]() Then
Then ![]() Therefore, there exist numbers
Therefore, there exist numbers ![]() and
and ![]() such
that if
such
that if ![]()
![]() then
then
![]() We choose arbitrary points
We choose arbitrary points ![]() and
and ![]() and
connect them by
a smooth curve
and
connect them by
a smooth curve ![]() such that
such that ![]() and
and ![]() This
curve can be selected such that
This
curve can be selected such that ![]() Then on
Then on ![]() inequality (7) holds. It is easy to prove that the function
inequality (7) holds. It is easy to prove that the function ![]() is continuous on
is continuous on ![]() and continuously differentiable except
a finite number of points. Moreover, for a complex-valued function of real
variable the inequality
and continuously differentiable except
a finite number of points. Moreover, for a complex-valued function of real
variable the inequality ![]() holds except
points, where
holds except
points, where ![]() Then, in view of (7), we have
Then, in view of (7), we have
where ![]() Integrating
over the variable
Integrating
over the variable ![]() we deduce
we deduce
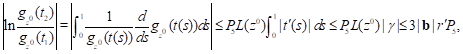 i.e.
i.e. ![]() We
can choose
We
can choose ![]() such that
such that ![]() Hence,
Hence,
| (9) |
Since ![]() and
and
![]() for all
for all ![]() by
Cauchy's inequality in variable
by
Cauchy's inequality in variable ![]() we obtain
we obtain
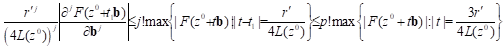 that is
that is ![]() (10)
(10)
Inequalities (9) and (10) imply that
where ![]() Hence,
Hence,
![]() Therefore, by Theorem A, the function
Therefore, by Theorem A, the function ![]() has a bounded
has a bounded ![]() -index
in the direction
-index
in the direction ![]() And by Theorem 3 from [1] the function
And by Theorem 3 from [1] the function ![]() is of the bounded
is of the bounded ![]() -index in the direction
-index in the direction ![]() too.
too.
Remark 1. We
require validity of (5) for
some ![]() but nor for all positive
but nor for all positive ![]() Thus, Theorem 1 improves the
corresponding theorem from [1, 4]. The proposition is new even in the
one-dimensional case (see results for the bounded
Thus, Theorem 1 improves the
corresponding theorem from [1, 4]. The proposition is new even in the
one-dimensional case (see results for the bounded ![]() -index
in [6] and bounded index in [8]).
-index
in [6] and bounded index in [8]).
4. Boundedness of l-index of entire
solutions of the equation ![]()
We denote ![]()
![]()
![]()
Theorem 2. Let ![]()
![]() be
an entire function of bounded
be
an entire function of bounded ![]() -index in the
directions
-index in the
directions ![]() for every
for every ![]() If
there exist
If
there exist ![]() and
and ![]() such
that
such
that
![]() for all
for all ![]() , then any entire solution w(z) of (3) has a bounded l-index.
, then any entire solution w(z) of (3) has a bounded l-index.
Proof: Differentiating (3) in variable ![]() and using Theorem B we obtain that for all
and using Theorem B we obtain that for all ![]()
Hence, ![]() This inequality is
similar to (6). Repeating arguments from Theorem 1, we
deduce that
This inequality is
similar to (6). Repeating arguments from Theorem 1, we
deduce that ![]() has a bounded l-index.
Theorem 2 is proved.
has a bounded l-index.
Theorem 2 is proved.
As application of the theorem we consider the differential equation:
| (11) |
Corollary 1.
Let ![]() be entire function of bounded
be entire function of bounded
![]() -index,
-index, ![]()
![]() Then every entire function satisfying (11)
has
a bounded
Then every entire function satisfying (11)
has
a bounded ![]() -index.
-index.
5. The linear homogeneous differential equation with fast growing coefficients
As in [10], let ![]() be a
strictly increasing positive unbounded function on
be a
strictly increasing positive unbounded function on ![]()
![]() be an inverse function to
be an inverse function to ![]()
![]() We
define the order of the growth of an entire function
We
define the order of the growth of an entire function ![]()
![]() and the function
and the function ![]()
![]() where
where ![]() ,
, ![]() is chosen such that
is chosen such that ![]() And also we need the greater function
And also we need the greater function ![]()
![]() where
where ![]() is chosen such that
is chosen such that ![]() Let
Let ![]() be the class of positive
continuously differentiable on
be the class of positive
continuously differentiable on ![]() functions
functions ![]() such that
such that ![]() as
as ![]() We need the following proposition of
Bordulyak:
We need the following proposition of
Bordulyak:
Theorem G [9]. Let
![]() and entire functions
and entire functions ![]()
![]()
![]() satisfy the condition
satisfy the condition ![]()
![]() for
all
for
all ![]()
![]() If
an entire function
If
an entire function ![]() is a solution of (4) then
is a solution of (4) then ![]() is of the bounded
is of the bounded
![]() -index and
-index and
Theorem 3. Let
![]() be a strictly increasing positive
unbounded function on
be a strictly increasing positive
unbounded function on ![]() If
If ![]()
![]() every entire function
every entire function ![]() has a bounded
has a bounded
![]() -index (
-index (![]() )
then every entire function satisfying (4) has a bounded
)
then every entire function satisfying (4) has a bounded
![]() -index. If, in addition,
-index. If, in addition, ![]()
![]() is a
continuously differentiable function of real variable
is a
continuously differentiable function of real variable ![]() then
then
| (12) |
for every entire transcendental
function ![]() satisfying (4).
satisfying (4).
Proof: Since ![]() , the following inequalities hold
, the following inequalities hold ![]() for
arbitrary
for
arbitrary ![]()
![]() and
and ![]() It means that
It means that ![]() Denote
Denote
![]() Hence, for
Hence, for ![]() one
has
one
has
i.e. (5) is valid for ![]() By Theorems D and 1 entire solutions of (4) have
a bounded
By Theorems D and 1 entire solutions of (4) have
a bounded ![]() -index. It is easy to prove
that for all
-index. It is easy to prove
that for all ![]()
![]() Thus,
by Theorem 3 from [1], an entire function
Thus,
by Theorem 3 from [1], an entire function ![]() satisfying (4) is of the
bounded
satisfying (4) is of the
bounded
![]() -index, too. The
function
-index, too. The
function ![]() is a strictly increasing and continuously differentiable function of a real
variable. Then
is a strictly increasing and continuously differentiable function of a real
variable. Then ![]() Furthermore,
Furthermore, ![]() as
as ![]() Using
Theorem F we obtain (12).
Using
Theorem F we obtain (12).
Theorem 4. Let
![]() be a strictly increasing positive
unbounded and continuously differentiable function on
be a strictly increasing positive
unbounded and continuously differentiable function on ![]() If
If
![]()
![]()
![]() as
as ![]() then
every entire function satisfying (4) has a bounded
then
every entire function satisfying (4) has a bounded
![]() -index and
-index and
Proof: At first, we prove that ![]() Indeed,
Indeed,
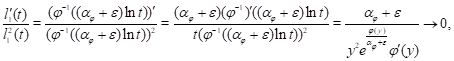 |
where ![]() as
as ![]() As
above, one has
As
above, one has ![]() Hence,
Hence, ![]() Thus,
Thus,
![]() and
and ![]() satisfy
conditions of Theorem G with
satisfy
conditions of Theorem G with ![]() Therefore, every entire function
satisfying (4) has a bounded
Therefore, every entire function
satisfying (4) has a bounded ![]() -index.
-index.
These theorems are a refinement of results of
M. Bordulyak, A. Kuzyk and
M. Sheremeta [6, 9]. Unlike these authors, we define the specific function ![]() such that entire solutions have a bounded
such that entire solutions have a bounded ![]() -index.
But the function
-index.
But the function ![]() depends of the function
depends of the function ![]() Below, we will
construct functions
Below, we will
construct functions ![]() and
and ![]() for the entire transcendental function
for the entire transcendental function ![]() of infinite order.
of infinite order.
Theorem 5. For
an arbitrary continuous right differentiable on ![]() function
function
![]() such that
such that ![]() there
exists a convex on
there
exists a convex on ![]() function
function ![]() with the properties (i)
with the properties (i) ![]() ,
, ![]() ; (ii)
; (ii) ![]() for
an unbounded from above set of values
for
an unbounded from above set of values ![]() .
.
Proof: For a given ![]() we
put
we
put ![]() and
and ![]() Clearly, the function
Clearly, the function ![]() is continuous on
is continuous on ![]() and
and ![]() is fully
contained in a range of this function. For every
is fully
contained in a range of this function. For every ![]() there exists
there exists ![]() such
that
such
that ![]() and
and ![]() for
all
for
all ![]() . Given the above, it is easy to justify
the existence of increasing to
. Given the above, it is easy to justify
the existence of increasing to ![]() sequence
sequence ![]() , for which: 1)
, for which: 1) ![]() ; 2) a sequence
; 2) a sequence ![]() is increasing to
is increasing to ![]() , where
, where ![]() for
every
for
every ![]() ; 3)
; 3) ![]() for all
for all ![]() and
every
and
every ![]() .
.
Let ![]() and
and ![]() for
for ![]() .
Clearly, that
.
Clearly, that ![]() is a nondecreasing on
is a nondecreasing on ![]() function. Hence, a function
function. Hence, a function ![]() is convex on
is convex on ![]() . For this function
we have
. For this function
we have ![]() and for every
and for every ![]()
![]()
![]()
![]()
i.e. (ii) holds. If ![]() for
some
for
some ![]() , then we obtain
(i):
, then we obtain
(i):
This follows from Theorem 5 that ![]() ,
, ![]() .
.
Theorem 6. For
an arbitrary entire transcendental function ![]() of
infinite order there exists a convex on
of
infinite order there exists a convex on ![]() function
function
![]() such that 1)
such that 1) ![]()
![]() 2)
2) ![]() for
an unbounded from the above set of values
for
an unbounded from the above set of values ![]() 3)
3) ![]()
![]()
Proof: We put ![]() ,
, ![]() .
Since
.
Since ![]() is of infinite order, it follows
is of infinite order, it follows ![]() .
Let
.
Let ![]() be a function constructed for the
function
be a function constructed for the
function ![]() in Theorem 5. Denote
in Theorem 5. Denote ![]()
![]() . Then
. Then ![]()
![]() . It means that
the function
. It means that
the function ![]() is a convex increasing on half-bounded interval
is a convex increasing on half-bounded interval
![]() , where
, where ![]() . We
put
. We
put ![]() for
for ![]() and
and ![]() for
for ![]() . By Theorem 5
assumptions 1) and 2) hold. We also obtain
. By Theorem 5
assumptions 1) and 2) hold. We also obtain![]()
![]() . Therefore, 3) is true.
. Therefore, 3) is true.
Let ![]() where
where ![]() is chosen such that
is chosen such that ![]()
Theorem 7. For
an arbitrary entire transcendental function ![]() of
infinite order there exists a strictly increasing positive unbounded and
continuously differentiable function
of
infinite order there exists a strictly increasing positive unbounded and
continuously differentiable function ![]() on
on ![]() with
with ![]() And
if
And
if ![]() where
where ![]() then
then ![]()
Proof: In view of Theorem 6
we choose ![]() where
where ![]() is
an inverse function to
is
an inverse function to ![]() Then
Then ![]() It is obvious that the function
It is obvious that the function ![]() is a strictly increasing positive unbounded and
is a strictly increasing positive unbounded and ![]() Besides,
Besides, ![]() is a
continuously differentiable function except for the
points of discontinuity of
is a
continuously differentiable function except for the
points of discontinuity of ![]() We
estimate a logarithmic derivative of
We
estimate a logarithmic derivative of ![]() :
:
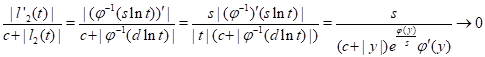 |
where ![]() as
as ![]() It implies that
It implies that
![]() .
.
6. Conclusions
Note that a concept of the bounded ![]() -index in a direction has a few
advantages in the comparison with traditional approaches to study the
properties of entire solutions of differential equations. In particular, if an
entire solution has a bounded index, then it immediately yields its growth
estimates, a uniform in a some sense distribution of its zeros, a certain
regular behavior of the solution, etc.
-index in a direction has a few
advantages in the comparison with traditional approaches to study the
properties of entire solutions of differential equations. In particular, if an
entire solution has a bounded index, then it immediately yields its growth
estimates, a uniform in a some sense distribution of its zeros, a certain
regular behavior of the solution, etc.
References
[1]
Bandura A.I., Skaskiv O.B., Entire functions of
bounded ![]() -index in direction, Mat. Stud. 2007, 27,
1, 30-52 (in Ukrainian).
-index in direction, Mat. Stud. 2007, 27,
1, 30-52 (in Ukrainian).
[2]
Bandura A.I., Skaskiv O.B., Sufficient sets for
boundedness ![]() -index in direction for entire
functions, Mat. Stud. 2007, 30, 2, 30-52.
-index in direction for entire
functions, Mat. Stud. 2007, 30, 2, 30-52.
[3] Bandura A.I., Skaskiv O.B., Open problems for entire functions of bounded index in direction, Mat. Stud. 2015, 43, 1, 103-109. dx.doi.org/10.15330/ms.43.1.103-109.
[4] Bandura A., Skaskiv O., Entire functions of several variables of bounded index, Lviv, Chyslo, Publisher I.E. Chyzhykov 2016, 128 p.
[5]
Kuzyk A.D., Sheremeta M.M., Entire functions of
bounded ![]() -distribution of values, Math. Notes
1986, 39, 1, 3-8.
-distribution of values, Math. Notes
1986, 39, 1, 3-8.
[6] Kuzyk A.D., Sheremeta M.N., On entire functions, satisfying linear differential equations, Diff. Equations 1990, 26, 10, 1716-1722. (in Russian).
[7] Fricke G.H., Shah S.M., Entire functions satisfying a linear differential equation, Indag. Math. 1975, 37, 39-41.
[8] Fricke G.H., Shah S.M., On bounded value distribution and bounded index Nonlinear Anal. 1978, 2, 4, 423-435.
[9] Bordulyak M.T., On the growth of entire solutions of linear differential equations, Mat. Stud. 2000, 13, 2, 219-223.
[10] Cao T.-B., Complex oscillation of entire solutions of higher-order linear differential equations, Electronic Journal of Differential Equations 2006, 81, 1-8.
[11] Chen Z.X., Yang C.C., Quantitative estimations on the zeros and growth of entire solutions of linear differential equations, Complex Variables 2000, 42, 119-133.
[12] Hamani K., Belaїdi B., Growth of solutions of complex linear differential equations with entire coefficients of finite iterated order, Acta Universitatis Apulensis 2011, 27, 203-216.
[13] Heittokangas J., Korhonen R., Rattyä J., Growth estimates for analytic solutions of complex linear differential equations, Ann. Acad. Sci. Fenn. Math. 2004, 29, 233-246.
[14] Kinnunen L., Linear differential equations with solutions of finite iterated order, Southeast Asian Bull. Math. 1998, 22, 385-405.
[15] Lin J., Tu J., Shi L.Z., Linear differential equations with entire
coefficients of ![]() -order in the complex plane,
J. Math. Anal. Appl. 2010, 372, 55-67.
-order in the complex plane,
J. Math. Anal. Appl. 2010, 372, 55-67.
[16] Chyzhykov I., Semochko N., Fast growing enitre solutions of linear differential equations, Math. Bull. Shevchenko Sci. Soc. 2016, 13, 68-83.
[17] Sheremeta M., Analytic Functions of Bounded Index, VNTL Publishers, Lviv 1999, 142 p.


