Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime
Mikhail Matalytski
,Victor Naumenko
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Matalytski_2017,
doi = {10.17512/jamcm.2017.1.09},
url = {https://doi.org/10.17512/jamcm.2017.1.09},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {1},
pages = {97--108},
author = {Mikhail Matalytski and Victor Naumenko},
title = {Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.1.09 UR - https://doi.org/10.17512/jamcm.2017.1.09 TI - Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Matalytski, Mikhail AU - Naumenko, Victor PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 97 EP - 108 IS - 1 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Matalytski, M., & Naumenko, V. (2017). Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime. Journal of Applied Mathematics and Computational Mechanics, 16(1), 97-108. doi:10.17512/jamcm.2017.1.09
Matalytski, M. & Naumenko, V., 2017. Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime. Journal of Applied Mathematics and Computational Mechanics, 16(1), pp.97-108. Available at: https://doi.org/10.17512/jamcm.2017.1.09
[1]M. Matalytski and V. Naumenko, "Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 1, pp. 97-108, 2017.
Matalytski, Mikhail, and Victor Naumenko. "Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime." Journal of Applied Mathematics and Computational Mechanics 16.1 (2017): 97-108. CrossRef. Web.
1. Matalytski M, Naumenko V. Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(1):97-108. Available from: https://doi.org/10.17512/jamcm.2017.1.09
Matalytski, Mikhail, and Victor Naumenko. "Analysis of the queueing network with a random bounded waiting time of positive and negative customers at a non-stationary regime." Journal of Applied Mathematics and Computational Mechanics 16, no. 1 (2017): 97-108. doi:10.17512/jamcm.2017.1.09
ANALYSIS OF THE QUEUEING NETWORK WITH A RANDOM BOUNDED WAITING TIME OF POSITIVE AND NEGATIVE CUSTOMERS AT A NON-STATIONARY REGIME
Mikhail Matalytski 1, Victor Naumenko 2
1 Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
2 Faculty of Mathematics and Computer
Science, Grodno State University
Grodno, Belarus
m.matalytski@gmail.com, victornn86@gmail.com
Received: 14 October 2016; accepted:
17 November 2016
Abstract. In the first part of the article, an investigation of an open Markov queueing network with positive and negative customers (G-networks) has been carried out. The network receives two exponential arrivals of positive and negative customers. Negative customers do not receive service. The waiting time of customers of both types in each system is bounded by a random variable having an exponential distribution with different parameters. When the waiting time of a negative customer in the queue is over it reduces the number of positive customers per unit if the system has positive customers. The Kolmogorov system of difference-differential equations for non-stationary state probabilities has been derived. The method for finding state probabilities of an investigated network, based on the use of apparatus of multidimensional generating functions has been proposed. Expressions for finding the mean number of positive and negative customers in the network systems have also been found. In the second part the same network has been investigated, but with revenues. The case when revenues from the network transitions between states are random variables with given mean values has been considered. A method for finding expected revenues of the network systems has been proposed. Obtained results may be used for modeling of computer viruses in information systems and networks and also for forecasting of costs, considering the viruses penetration.
MSC 2010: 49K45, 60K20
Keywords: G-network, positive and negative customers, random bounded waiting time of customers, non-stationary regime, generation function, non-stationary state probabilities, expected revenues
1. Introduction
Queueing Networks (QN) with negative customers and other features cause a special interest of researchers. Negative customers differ from ordinary customers in that they require no service and have an impact on the state of the queueing system (QS). They reduce a queue of ordinary customers of a nonempty QS per [1].
In the present article, we consider an open QN, in which two simple streams of positive and negative customers arrive. Services require only positive customers. The waiting time in the queue for positive and negative customers is bounded by the random variables having an exponential distribution with different parameters. A negative customer, by the end of waiting time, reduces the count of positive customers in the system by unity, if there is such a system.
This assumption can find its application in modeling the behavior of information systems and networks. When transferring a query (positive requests) there is often a break or pause established, after which it means that the transfer request does not fit in the planned time interval, after which the request is removed from the queue. Negative customers in the model can describe the viruses in the system, which start acting through a random time and destroy positive customers in the system.
Recently, attention has been paid to the study of Markov chains with revenues (HM-networks), and various features, for example with a bounded waiting time of customers [2], or positive and negative customers [3]. This article discusses a few more of these features. Namely, the presence in a Markov network with revenues of negative customers and a bounded waiting time of positive and negative customers in network systems.
In other words, we investigate the synthesis of QN-HM-networks [4] with positive and negative customers. While waiting time of such customers in each system are bounded by the random variables. We consider the case when the revenue from the network transitions between states are random variables with given mean values.
2. Network description. Problem formulation
Consider an open G-network [1] with ![]() single-queues QS. An independent Poisson flow of positive customers with
rate
single-queues QS. An independent Poisson flow of positive customers with
rate ![]() and a Poisson flow of negative customers with rate
and a Poisson flow of negative customers with rate ![]() arrive to QS
arrive to QS ![]() from
outside (system
from
outside (system ![]() ),
), ![]() All
customer flows arriving to QS are assumed to be independent. A positive
customer arriving to the system increases the count of customers in the system
by unity and requires service. Requests are serviced in the order received.
Service times of
customers in the i-th QS independent, not dependent on the receipt of
the processes and for positive
customers have an exponential distribution with rate
All
customer flows arriving to QS are assumed to be independent. A positive
customer arriving to the system increases the count of customers in the system
by unity and requires service. Requests are serviced in the order received.
Service times of
customers in the i-th QS independent, not dependent on the receipt of
the processes and for positive
customers have an exponential distribution with rate ![]() where ki-count
of positive customers in the i-th QS
where ki-count
of positive customers in the i-th QS ![]() Each
positive customer,
located in the system, has a waiting time bounded exponentially distributed
random variable with rate
Each
positive customer,
located in the system, has a waiting time bounded exponentially distributed
random variable with rate ![]() for
for ![]()
![]() and it does not depend on other
factors for example waiting time of other customers in the queue,
and it does not depend on other
factors for example waiting time of other customers in the queue, ![]()
A negative customer, arriving to QS,
increases the length of the queue of negative customers for one, and requires
no service. Each negative customer, located
in i-th QS, stays in the queue for a random time according to a Poisson
process of rate ![]() for
for ![]() where
li-count of
negative customers in i-th QS,
where
li-count of
negative customers in i-th QS, ![]()
![]() By the end of this time, the negative
customer destroys one positive customer in the QS
By the end of this time, the negative
customer destroys one positive customer in the QS ![]() and
leaves the network. If after this random time in the system there are no
positive customers, then a given negative customer leaves the network, without
exerting any influence on the operation of the network as a whole. Wherein the
probability that in QS
and
leaves the network. If after this random time in the system there are no
positive customers, then a given negative customer leaves the network, without
exerting any influence on the operation of the network as a whole. Wherein the
probability that in QS ![]() a negative customer leaves
the queue during
a negative customer leaves
the queue during ![]() on the condition that, in
this QS at time
on the condition that, in
this QS at time ![]() there are
there are ![]() negative customers, equals
negative customers, equals ![]()
![]()
If at time ![]() positive
customer is located on servicing in the i-th system, then on interval
positive
customer is located on servicing in the i-th system, then on interval ![]() it will finish service with probability
it will finish service with probability
![]()
![]() If on interval
If on interval ![]() the waiting time of customer
in the queue of i-th QS is up, then it leaves the queue with probability
the waiting time of customer
in the queue of i-th QS is up, then it leaves the queue with probability
![]()
![]()
The positive customer gets serviced in ![]() with probability
with probability ![]() move to QS
move to QS ![]() as a
positive customer and with probability
as a
positive customer and with probability ![]() - as
a negative customer and with probability
- as
a negative customer and with probability
![]() come out of the network to the external environ-
ment,
come out of the network to the external environ-
ment, ![]()
A positive customer, waiting time of which in
the queue of i-th QS has expired, move to j-th system with probability
![]() as a positive customers, and with
probabil-
ity
as a positive customers, and with
probabil-
ity ![]() as a negative customer, and with a
probability
as a negative customer, and with a
probability ![]() leave the network.
leave the network.
The network state at time ![]() described by the vector
described by the vector ![]() which forms a homogeneous Markov process with a countable count of
states, where the state
which forms a homogeneous Markov process with a countable count of
states, where the state ![]() means that at time
means that at time ![]() in QS
in QS ![]() there
are
there
are ![]() positive customers and
positive customers and ![]() negative customers,
negative customers, ![]()
In the first part of the article we shall find probabilities of the network states, and the mean number of customers in the systems at the transient regime.
3. The system of the Kolmogorov difference-differential equations for the network state probabilities
We introduce some notations. Let ![]() - vector, which is i-th component equal to 1, all the others are 0,
- vector, which is i-th component equal to 1, all the others are 0, ![]()
![]() - state probability
- state probability ![]() at moment time
at moment time ![]()
![]() - Heaviside function,
- Heaviside function, ![]() .
.
The possible transitions of our Markov
process in the state ![]() during time
during time ![]()
– from
the state ![]() in this case into QS
in this case into QS ![]() for the time
for the time ![]() a
positive customer will arrive with probability
a
positive customer will arrive with probability ![]()
![]()
– from
the state ![]() while to the i-th QS for the
time
while to the i-th QS for the
time ![]() a negative customer will arrive with
probability
a negative customer will arrive with
probability ![]()
![]()
– from
the state ![]() in this case the positive customer
after servicing or at the end of waiting time (timeout) in the i-th QS,
comes out of the network to the external environment with probability
in this case the positive customer
after servicing or at the end of waiting time (timeout) in the i-th QS,
comes out of the network to the external environment with probability ![]()
![]()
– from
the state ![]() in the given case into i-th QS
after timeout
of negative customer it destroys in the QS the positive customer, the
probability of such an event is equal to
in the given case into i-th QS
after timeout
of negative customer it destroys in the QS the positive customer, the
probability of such an event is equal to ![]()
![]()
– from
the state ![]() while in the i-th QS the
residence time in the queue of the negative customer finished, if in time
while in the i-th QS the
residence time in the queue of the negative customer finished, if in time ![]() there were
there were ![]() negative
customers and there were no positive customers; the probability of such
an event is equal to
negative
customers and there were no positive customers; the probability of such
an event is equal to ![]() ,
, ![]()
– from
the state ![]() in a given case after finishing the
service
or timeout of the positive customer in the i-th QS it moves to
the j-th QS again as a positive
customer with probability
in a given case after finishing the
service
or timeout of the positive customer in the i-th QS it moves to
the j-th QS again as a positive
customer with probability ![]()
![]()
– from the state ![]() in this case after finishing the service
or timeout of the positive customer, in i-th QS it moves to the j-th
QS as
a negative customer; the probability of such an event is equal to
in this case after finishing the service
or timeout of the positive customer, in i-th QS it moves to the j-th
QS as
a negative customer; the probability of such an event is equal to ![]()
![]()
– from
the state ![]() while in each i-th QS,
while in each i-th QS, ![]() no positive nor any negative customers
arrive, and in which for the time
no positive nor any negative customers
arrive, and in which for the time ![]() no customer not have
been serviced, no negative customer will come out of the queue; the probability
of such event is equal to
no customer not have
been serviced, no negative customer will come out of the queue; the probability
of such event is equal to
![]()
![]()
– from other states with probability ![]() .
.
We will assume that the service and waiting
time of positive customers in the
i-th QS has an exponential distribution with the rate ![]() and
and ![]() respectively, but the waiting time of negative customers in the i-th QS -
an exponential distribution with the rate
respectively, but the waiting time of negative customers in the i-th QS -
an exponential distribution with the rate ![]() Consequently, in this case
Consequently, in this case ![]()
![]()
![]()
![]() Then, using the formula of
total probability, we can
obtain, as previously for other networks [3], in this case the system of
difference-differential equations for the non-stationary state probabilities of
the considered network:
Then, using the formula of
total probability, we can
obtain, as previously for other networks [3], in this case the system of
difference-differential equations for the non-stationary state probabilities of
the considered network:
![]()
![]()
![]() (1)
(1)
![]()
![]() .
.
4. Finding the state probabilities and the mean number of customers in the queueing system
Denote by ![]() where
where ![]() the generating function of the dimension of
the generating function of the dimension of ![]()
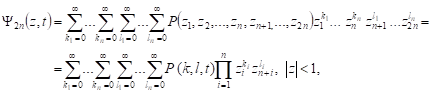 | (2) |
the summation is taking for each ![]()
![]() from
0 to
from
0 to ![]()
![]() We
will assume that
We
will assume that ![]()
![]()
![]()
![]()
Multiplying
each of the equations (1) to ![]() and summing up all possible values
and summing up all possible values ![]() and
and ![]() from
1 to
from
1 to ![]()
![]() Here
the summation for all
Here
the summation for all ![]() and
and ![]() is
taken from 1 to
is
taken from 1 to ![]() i. e. all summands in
(1), for which in the network state
i. e. all summands in
(1), for which in the network state ![]() there are components
there are components ![]() and
and ![]() due to the assumptions put forward above. Because, for
example
due to the assumptions put forward above. Because, for
example ![]()
![]() Then
we obtain
Then
we obtain
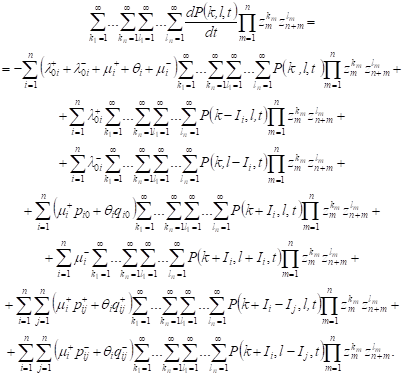 | (3) |
Using (3), we can show that for a multidimensional generating function there is a valid homogeneous linear differential equation, the general solution having the form
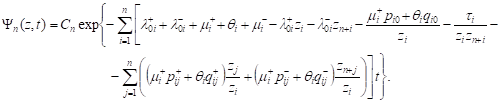 |
Let’s consider, that at the initial moment of
time, the network is in a state ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Then the initial condition for the last equation will be
from which we obtain ![]()
Theorem. If at the initial moment of time the QN is in a state ![]()
![]()
![]()
![]() then
the expression for the generating function
then
the expression for the generating function ![]() taking
into account the expansions appearing in it exponent Maclaurin, has
the form
taking
into account the expansions appearing in it exponent Maclaurin, has
the form
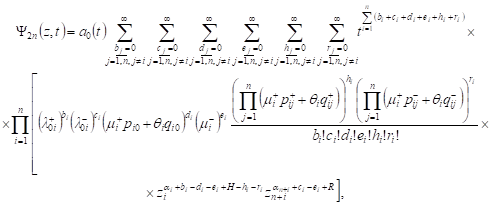 | (4) |
where
The theorem is proved similarly as, for example, in the works [3, 4].
With the obtained
expression for the generating function can be found
state probabilities of the considered network. State probability of ![]() is the coefficient at
is the coefficient at ![]() in
the expansion of (2) in multiple series (4), on condition, that at the initial
time
the network is in a state
in
the expansion of (2) in multiple series (4), on condition, that at the initial
time
the network is in a state ![]()
Remark. If the waiting time of positive customers not to bound by a random variable, then we obtain results similar to those that is in the work [3].
The mean number of the customers in the
network systems can be found, differentiating (4) by ![]() and
suppose
and
suppose ![]() Therefore for the mean number of
positive customers in the network system at time t in the QS with
the number x we will use the relation,
Therefore for the mean number of
positive customers in the network system at time t in the QS with
the number x we will use the relation, ![]()
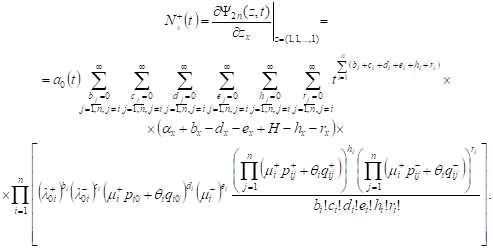 | (5) |
The change of variables will be done in the
expression (5) ![]() and considering, all network QS operating
under heavy-traffic regime, e.g.
and considering, all network QS operating
under heavy-traffic regime, e.g. ![]() and, consequently,
and, consequently, ![]() therefore obtain for all
therefore obtain for all ![]()
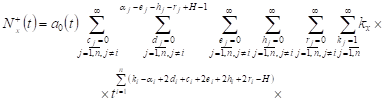 |
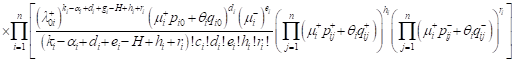 .
.
5. Analysis of the queueing networks with revenues
Let’s find the mean expected revenues, which
make customers of the i-th QS
of service in it. We assume, that service and waiting times of positive
customers
in the i-th QS has an
exponential distribution with rates ![]() and
and ![]() respectively, and waiting times in
the i-th QS of negative customers - an exponential distribution with rate
respectively, and waiting times in
the i-th QS of negative customers - an exponential distribution with rate ![]() In addition also assume, that all systems
operate under heavy-traffic regime, i.e.
In addition also assume, that all systems
operate under heavy-traffic regime, i.e. ![]()
![]()
![]() in this case
in this case ![]()
![]() In the simulation, the effect of the virus penetration into a computer
network or by a computer attacks on it takes place just such a situation. In
this case the busy
period of QS is infinite and, therefore, the stationary distribution does not
exist,
the load factor of QS exceeds unity. However, it should be noted that in these
conditions various real objects may operate on most time intervals.
In the simulation, the effect of the virus penetration into a computer
network or by a computer attacks on it takes place just such a situation. In
this case the busy
period of QS is infinite and, therefore, the stationary distribution does not
exist,
the load factor of QS exceeds unity. However, it should be noted that in these
conditions various real objects may operate on most time intervals.
Consider
the dynamics of revenue changes of the i-th QS, ![]() Let at the ini-
tial moment of time the income of this QS be equal to
Let at the ini-
tial moment of time the income of this QS be equal to ![]()
![]() We are inter-
ested in income
We are inter-
ested in income ![]() at time t. The income
of its QS at moment time
at time t. The income
of its QS at moment time ![]() can be represented
in the form
can be represented
in the form
| (6) |
where ![]() - revenue changes of
the i-th system at the time interval
- revenue changes of
the i-th system at the time interval ![]()
![]() To find the revenues of the i-th
QS we write the conditional probabilities of the events that may occur during
To find the revenues of the i-th
QS we write the conditional probabilities of the events that may occur during ![]()
![]() The
following cases are possible:
The
following cases are possible:
– with
probability ![]() to the i-th QS from the external
environment
a positive customer will arrive, which will bring a revenue in the amount of
to the i-th QS from the external
environment
a positive customer will arrive, which will bring a revenue in the amount of ![]() where
where ![]() - random variable (RV)
with expectation (E) of which equals
- random variable (RV)
with expectation (E) of which equals ![]()
![]()
– with
probability ![]() to the i-th QS from the external
environment
a negative customer will arrive,
to the i-th QS from the external
environment
a negative customer will arrive, ![]() revenue change of
the system in this case does not occur;
revenue change of
the system in this case does not occur;
– with probability ![]() a positive customer after servicing
or at the end of waiting time (timeout) in the i-th QS, comes out
of the network to the external environment, while a revenue of the i-th
QS decreases by
an amount
a positive customer after servicing
or at the end of waiting time (timeout) in the i-th QS, comes out
of the network to the external environment, while a revenue of the i-th
QS decreases by
an amount ![]() where
where ![]() - RV with
- RV with ![]()
![]()
– with
probability ![]() to the i-th QS after timeout of
negative customer it destroys the positive customer in the QS and leaves the
network,
to the i-th QS after timeout of
negative customer it destroys the positive customer in the QS and leaves the
network, ![]() in this case a revenue of the i-th QS decreases by an amount
in this case a revenue of the i-th QS decreases by an amount ![]() where
where ![]()
![]()
– after
finishing the service or timeout of the positive customer in the i-th QS
it moves to the j-th QS again as a positive customer with probability ![]()
![]() by
such a transition a revenue of the i-th QS decreases by an amount
by
such a transition a revenue of the i-th QS decreases by an amount ![]() and revenue of the j-th QS will
increase by this amount, where
and revenue of the j-th QS will
increase by this amount, where ![]()
![]()
– if
in the j-th QS there is a positive customer, service time or waiting
which
ended, then after the termination of it service in the j-th
QS it moves to the i-th QS again as a positive customer with probability ![]() while a revenue of the i-th QS decreases by an amount
while a revenue of the i-th QS decreases by an amount ![]() and revenue of
the j-th QS will increase by this amount, where
and revenue of
the j-th QS will increase by this amount, where ![]()
![]()
– with probability ![]() service time or waiting time of
the positive customer ended in the i-th QS and it, after
finishing the service
in the i-th QS, moves to the j-th QS as a negative customer,
service time or waiting time of
the positive customer ended in the i-th QS and it, after
finishing the service
in the i-th QS, moves to the j-th QS as a negative customer, ![]() by such a transition a revenue of the
i-th QS decreases by an amount
by such a transition a revenue of the
i-th QS decreases by an amount ![]() and revenue of the j-th QS
will not occur, where
and revenue of the j-th QS
will not occur, where ![]()
![]()
– with probability
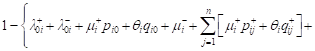
![]()
on the time interval ![]() state
changes of the i-th system will not happen,
in this case a revenue of the i-th system may increase (decrease) by the
value
state
changes of the i-th system will not happen,
in this case a revenue of the i-th system may increase (decrease) by the
value ![]() where
where ![]()
![]()
Then we get, that revenue changes of the i-th
system on the time interval ![]() can be written as
can be written as
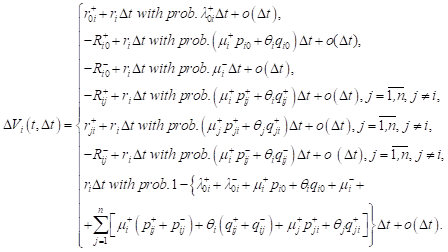 (7)
(7)
For
practical reasons, we may assume that all values ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() are
bounded. Then in view of (6) and (7) for the expectation
can be written:
are
bounded. Then in view of (6) and (7) for the expectation
can be written:
![]()
![]()
![]()
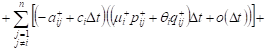
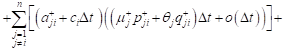
![]()
![]()
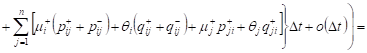
![]()
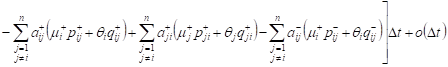 ,
,
i.e. ![]() where
where
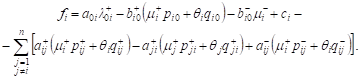 |
We
introduce the notation ![]() From (6) we have
From (6) we have ![]() from where, by going to the limit
from where, by going to the limit ![]() and
setting the initial conditions
and
setting the initial conditions ![]()
![]() we can find the expected revenues of
the network systems. This implies, that expected revenues
we can find the expected revenues of
the network systems. This implies, that expected revenues ![]() are linear functions of time:
are linear functions of time: ![]()
![]()
6. Conclusions
In the paper, the Markov G-network with a random bounded waiting time of positive and negative customers at a transient regime has been investigated. For such a network that operates under heavy-traffic regime, non-stationary state probabilities and relations for the mean number of customers with the help of the apparatus of multivariate generating functions has been founded. And a similar network with revenues has been considered. The expressions for the expected revenues of the network systems has been obtained.
Further investigations in this direction will be associated with obtaining similar results, taking into account falling into the signals (triggers) to the queueing network.
References
[1] Gelenbe E., Product form queueing networks with negative and positive customers, Journal of Applied Probability 1991, 28, 656-663.
[2] Matalytski M., Statkevich S., Stochastic Network with Bounded Waiting Time of Requests and Unreliable Service, GrSU, Grodno 2014.
[3] Matalytski M., Naumenko V., Stochastic Networks with Non-Standard Customers Movement, GrSU, Grodno 2016.
[4] Matalytski M., On some results in analysis and optimization of Markov networks with incomes and their applications, Automation and Remote Control. 2009, 70, 10, 1683-1697.


