Some remarks to the Jacobian Conjecture

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Lara-Dziembek_2017,
   doi = {10.17512/jamcm.2017.1.08},
   url = {https://doi.org/10.17512/jamcm.2017.1.08},
   year = 2017,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {16},
   number = {1},
   pages = {87--96},
   author = {Sylwia Lara-Dziembek and  Grzegorz Biernat and  Edyta Pawlak},
   title = {Some remarks to the Jacobian Conjecture},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2017.1.08
UR  - https://doi.org/10.17512/jamcm.2017.1.08
TI  - Some remarks to the Jacobian Conjecture
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Lara-Dziembek, Sylwia
AU  - Biernat, Grzegorz
AU  - Pawlak, Edyta
PY  - 2017
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 87
EP  - 96
IS  - 1
VL  - 16
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Lara-Dziembek, S., Biernat, G., & Pawlak, E. (2017). Some remarks to the Jacobian Conjecture. Journal of Applied Mathematics and Computational Mechanics, 16(1), 87-96. doi:10.17512/jamcm.2017.1.08

Lara-Dziembek, S., Biernat, G. & Pawlak, E., 2017. Some remarks to the Jacobian Conjecture. Journal of Applied Mathematics and Computational Mechanics, 16(1), pp.87-96. Available at: https://doi.org/10.17512/jamcm.2017.1.08

[1]S. Lara-Dziembek, G. Biernat and E. Pawlak, "Some remarks to the Jacobian Conjecture," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 1, pp. 87-96, 2017.

Lara-Dziembek, Sylwia, Grzegorz Biernat, and Edyta Pawlak. "Some remarks to the Jacobian Conjecture." Journal of Applied Mathematics and Computational Mechanics 16.1 (2017): 87-96. CrossRef. Web.

1. Lara-Dziembek S, Biernat G, Pawlak E. Some remarks to the Jacobian Conjecture. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(1):87-96. Available from: https://doi.org/10.17512/jamcm.2017.1.08

Lara-Dziembek, Sylwia, Grzegorz Biernat, and Edyta Pawlak. "Some remarks to the Jacobian Conjecture." Journal of Applied Mathematics and Computational Mechanics 16, no. 1 (2017): 87-96. doi:10.17512/jamcm.2017.1.08

SOME REMARKS TO THE JACOBIAN CONJECTURE

Sylwia Lara-Dziembek, Grzegorz Biernat, Edyta Pawlak

Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
sylwia.lara@im.pcz.pl, grzegorz.biernat@im.pcz.pl, edyta.pawlak@im.pcz.pl

Received: 11 January 2017; accepted: 9 March 2017

Abstract. This work is related to the Jacobian Conjecture. It contains the formulas concerning algebraic dependence of the polynomial mappings having two zeros at infinity and the constant Jacobian. These relations mean that such mappings are non-invertible. They reduce the Jacobian Conjecture only to the case of mappings having one zero at infinity. This case is already solved by Abhyankar. The formulas presented in the paper were illustrated by the large example.

MSC 2010: 14R15

Keywords: Jacobian, zero at infinity, Jacobian Conjecture

1. Introduction

In the paper [1], Abhyankar proved that the polynomial mapping with a constant non-zero Jacobian has at most two zeros at infinity. This result was generalized in the paper [2]. Moreover, in the same paper [1], Abhyankar also proved that the Jacobian Conjecture [3-7] holds if and only if from the assumption that it follows that the mapping F not has two zeros at infinity.

It is not difficult to indicate an infinite family of polynomial non-invertible mapping having two zeros at infinity. These examples can be generalized. Therefore, in this work, we indicate explicit formulas that give the algebraic dependence of coordinates of polynomial mapping when its Jacobian is constant. We consider two groups of mappings, depending on the form of the leading forms of these mappings. Therefore these formulas adjudicate that there are no polynomial invertible mappings having two zeros at infinity.

2. Algebraic dependence of polynomial mappings

Let f_i, h_j be the complex forms of variables X, Y of degrees i, j respectively and .

Remark 1. Let

(1)

and

(2)

where

If then

(3)

and

(4)

for some constants The form is defined by the formula .

Remark 2. Let

(5)

and

(6)

where (k and l are relativity prim) and .

If then exist the forms for which

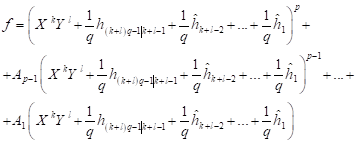(7)

and

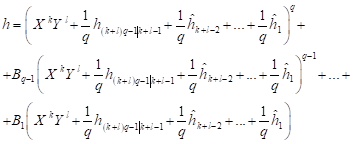(8)

for some constants The form of degree is defined by the formula .

The authors try to place the proofs of the above hypotheses in the next article.

Corollary. Obviously, in all of these possible cases, the polynomials f, h are algebraically dependent and so

The following example is the illustration of remark 2.

Example. Let

(9)

(10)

Since the Jacobian is constant we have consecutively

(11)

(12)

so

(13)

and appears

(14)

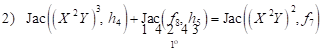(15)

where

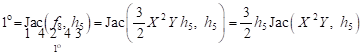(16)

therefore

(17)

and

(18)

Thus divides . We assume further that

(19)

which implies

(20)

returning to equality (18) we obtain

(21)

and occurs

(22)

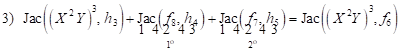(23)

where

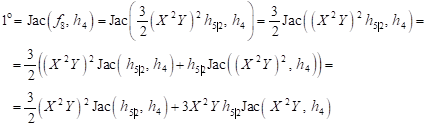(24)

and

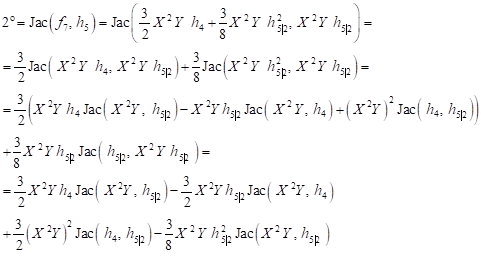
Of the equation (29) results

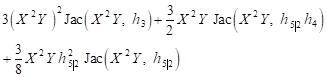(26)

so

(27)

and finally

(28)

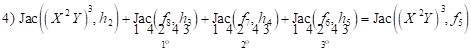(29)

Now we have

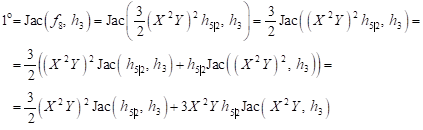(30)

Next

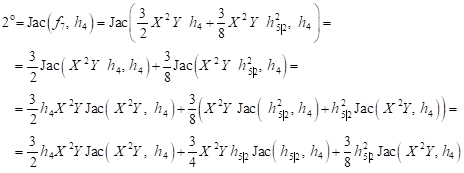(31)

and

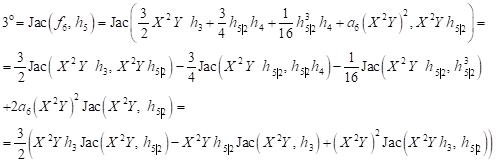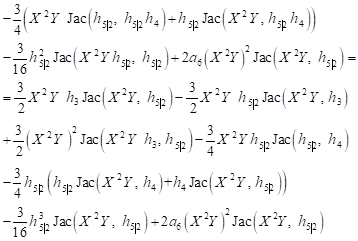(32)

Of the equation (29) results

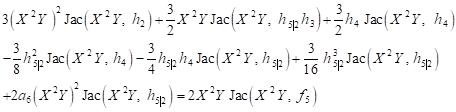(33)

hence

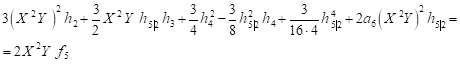(34)

and

(35)

Thus divides We assume again that

(36)

Therefore

(37)

From the equation (35) we obtain

(38)

The equality (36) defines the function which appears in remark 3. This means that the polynomials f and h will be the form

(39)

and

(40)

Consequently

(41)

(42)

and

(43)

Similarly

(44)

(45)

(46)

(47)

(48)

(49)

and

(50)

3. Conclusions

These hypotheses, tested by many examples, allow one to state that the polynomial mapping having two zeros at infinity are non-invertible (in the global sense). Therefore it remains necessary to analyze only the case when the mapping (f, h) has only one zero at infinity and thus takes the form

(51)

and

(52)

where are the forms (of two complex variables) of degrees i, j respectively.

We show that there are non-trivial class of mappings having one zero at infinity with the constant Jacobian, for which that Jacobian vanishes. It appears, therefore, that in the general case, the polynomial mapping having one zero at infinity and the constant Jacobian, must make the Jacobian vanish. This would mean that the Jacobian Conjecture takes place only in the case, when (cf. [1])

(53)

and

(54)

and also in the simplest case

(55)

(56)

The polynomials f, h have in each case one zero at infinity and do not have the constant components as well as .

References

[1] Abhyankar S.S., Expansion Techniques in Algebraic Geometry, Tata Inst. Fundamental Research, Bombay 1977.

[2] Charzyński Z., Chądzyński J., Skibinski P., A Contribution to Keller’s Jacobian Conjecture, Lecture Notes In Math. 1165, Springer-Verlag, Berlin, Heidelberg, New York 1985, 36-51.

[3] Wright D., On the Jacobian conjecture, Illinois J. Math. 1981, 25, 3, 423-440.

[4] Van den Essen A., Polynomial automorphisms and the Jacobian conjecture, Progress in Matematics 190, Birkhäuser Verlag, Basel 2000.

[5] Bass H., Connell E.H., Wright D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, American Mathematical Society. Bulletin. New Series 1982, 7(2), 287-330.

[6] Fulghesu D., An Introduction to the Jacobian Conjecture, Minnesota State University Moorhead, October 12, 2010.

[7] Drużkowski L.M., The Jacobian Conjecture, Uniwersytet Jagielloński, Kraków 1993.