Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method
Bohdan Kopytko
,Zhanneta Tsapovska
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Kopytko_2017,
doi = {10.17512/jamcm.2017.1.05},
url = {https://doi.org/10.17512/jamcm.2017.1.05},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {1},
pages = {51--62},
author = {Bohdan Kopytko and Zhanneta Tsapovska},
title = {Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.1.05 UR - https://doi.org/10.17512/jamcm.2017.1.05 TI - Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Kopytko, Bohdan AU - Tsapovska, Zhanneta PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 51 EP - 62 IS - 1 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Kopytko, B., & Tsapovska, Z. (2017). Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method. Journal of Applied Mathematics and Computational Mechanics, 16(1), 51-62. doi:10.17512/jamcm.2017.1.05
Kopytko, B. & Tsapovska, Z., 2017. Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method. Journal of Applied Mathematics and Computational Mechanics, 16(1), pp.51-62. Available at: https://doi.org/10.17512/jamcm.2017.1.05
[1]B. Kopytko and Z. Tsapovska, "Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 1, pp. 51-62, 2017.
Kopytko, Bohdan, and Zhanneta Tsapovska. "Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method." Journal of Applied Mathematics and Computational Mechanics 16.1 (2017): 51-62. CrossRef. Web.
1. Kopytko B, Tsapovska Z. Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(1):51-62. Available from: https://doi.org/10.17512/jamcm.2017.1.05
Kopytko, Bohdan, and Zhanneta Tsapovska. "Solution of one initial-boundary Wentzel problem for a parabolic equation with discontinuous coefficients by the boundary integral equation method." Journal of Applied Mathematics and Computational Mechanics 16, no. 1 (2017): 51-62. doi:10.17512/jamcm.2017.1.05
SOLUTION OF ONE INITIAL-BOUNDARY WENTZEL PROBLEM FOR A PARABOLIC EQUATION WITH DISCONTINUOUS COEFFICIENTS BY THE BOUNDARY INTEGRAL EQUATION METHOD
Bohdan Kopytko 1, Zhanneta Tsapovska 2
1 Institute
of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
2 Ivan Franko Lviv National University
Lviv, Ukraine
bohdan.kopytko@gmail.com, tzhannet@yahoo.com
Received: 11 January 2017; accepted:
10 March 2017
Abstract. In this article we consider the question of existence in the Holder
class of the solution of the initial-boundary problem for a linear parabolic
second-degree equation with discontinuous coefficients in noncylindrical
domain. This domain is bounded of the smooth elementary surfaces of the Holder
class ![]() .
The boundary conditions and the conjugation condition of the Wentzel type are
given to external and internal boundaries of
a domain respectively. We use the potential method to
solve this problem.
.
The boundary conditions and the conjugation condition of the Wentzel type are
given to external and internal boundaries of
a domain respectively. We use the potential method to
solve this problem.
MSC 2010: 35K20
Keywords: linear parabolic second-degree operator, potential method, conjugation condition of Wentzel type
1. Introduction
The theory of potentials is very important in the study of the Cauchy problem, the boundary-value problem, the conjugation problems for the heat equations and the general second-degree parabolic equations as well. The potential method is used to thoroughly examine the initial-boundary problems for the uniformly parabolic equations when the order of the differential boundary operators is less than the order of the equation in the domain [1-8]. We can encounter the initial-boundary problems which contain derivatives of the second and higher orders. The Wentzel problem is a vivid example of this type [9]. This is the initial-boundary problem for the parabolic equation with the boundary condition which has the form of a parabolic operator on the tangential variables. That problem arises, in particular, into the theory of Markov processes in the construction of a diffusion process in a domain on predetermined the diffusion coefficients and the boundary conditions.
The parabolic initial-boundary Wentzel problem (in a cylindrical domain) was investigated in the works [10-12] by the methods of functional analysis. In the papers [13, 14] (in cylindrical and noncylindrical domains) this problem was studied by the boundary integral equation method using a simple-layer potential. As for the parabolic problem with Wentzel conjugation conditions, this problem, for the case of a cylindrical domain, is studied in the most general formulation in the papers [15, 16].
In this article, we consider one of the problems in the assumption that the boundaries of the domains are the elementary noncylindrical surfaces of the Holder class.
2. Problem statement and its solution
In a
layer ![]() where
where ![]() is fixed,
is fixed, ![]()
![]() is the
is the
![]() -dimensional Euclidian space of the points
-dimensional Euclidian space of the points ![]()
![]() we consider the domain
we consider the domain ![]() with the smooth
boundary
with the smooth
boundary ![]() where
where ![]() ,
, ![]() We
assume, that the surface
We
assume, that the surface ![]() subdivides the
domain
subdivides the
domain ![]() into two domains
into two domains ![]() and
and ![]() with
the boundaries
with
the boundaries ![]()
![]() and
and ![]()
Let ![]()
![]()
![]()
![]()
![]() in particular by
in particular by ![]()
![]() we denote
we denote ![]() at
at ![]() By
By ![]() we denote the
unit normal vector at the point
we denote the
unit normal vector at the point ![]() to the surface
to the surface ![]()
![]() which is in the section
which is in the section ![]() and the vectors
and the vectors ![]() and
and
![]()
![]() directed
inwards to the domains
directed
inwards to the domains ![]() and
and ![]() respectively.
respectively.
![]() is the value of the function
is the value of the function ![]() on the surface
on the surface ![]()
![]() i.e.
i.e. ![]()
The differential operators with respect to ![]() and
and ![]() we denote by
we denote by ![]() and
and ![]()
![]()
![]() (
(![]() ) is a tangent differential operator on
) is a tangent differential operator on ![]()
![]() i.e.
i.e. ![]() where
where
![]()
![]()
![]() is the Kronecker symbol. If
is the Kronecker symbol. If ![]()
![]() then
then ![]()
Let ![]() and
and ![]() be any domains,
be any domains, ![]() and
and ![]() are the closure of them,
are the closure of them, ![]() and
and ![]() are some numbers,
are some numbers, ![]() is an integer and
is an integer and ![]()
Similar to [3, ch. I, § 1] ![]() is the class
surface,
is the class
surface, ![]() and
and ![]() are the
corresponding Holder spaces with the norms
are the
corresponding Holder spaces with the norms ![]() and
and ![]() which are defined on
which are defined on ![]() and
and ![]() respectively.
respectively. ![]() is the subspace
of functions from
is the subspace
of functions from ![]() that together with admissible derivative with respect to the time
variable, vanishes at
that together with admissible derivative with respect to the time
variable, vanishes at ![]()
![]()
![]() are positive constants independent of
are positive constants independent of ![]() We
are not interested in their specific value.
We
are not interested in their specific value.
In a layer ![]() let us consider
two second-order uniformly parabolic equations
let us consider
two second-order uniformly parabolic equations
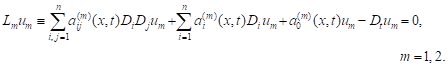 | (1) |
Assume that the coefficients of the operator ![]()
![]() are
defined in
are
defined in ![]() and the following assumptions are true:
and the following assumptions are true:
| (А1) |
Assumptions (A1), (A2) guarantee the
existence of a fundamental solution (f.s.) for each equation from (1) (see [3,
ch. IV, § 11]) which we will denote by ![]() (
(![]()
![]() ),
), ![]()
Let us consider the integrals - the parabolic simple-layer potentials:
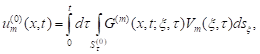 | (2) |
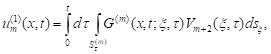 | (3) |
where the functions ![]() and
and ![]()
![]() defined, bounded
and continuous on surfaces
defined, bounded
and continuous on surfaces ![]() and
and ![]() respectively.
respectively.
We note some properties of the potential (2),
(3) (see [1-4]). The functions (2) and (3) satisfy the equation (1) at each point ![]() and
and ![]() respectively,
and they also satisfy the initial condition
respectively,
and they also satisfy the initial condition ![]()
![]()
![]()
![]()
At the points of the surfaces ![]() and
and ![]()
![]() let the conormal vectors
let the conormal vectors ![]()
![]() and
and ![]()
![]() where
where ![]()
![]() be defined. The important property of
the simple-layer potential reflected in the boundary relations for the conormal
derivative of this potential (see [2, ch. V, § 2], [3, ch. IV, § 15], [4, 5]).
be defined. The important property of
the simple-layer potential reflected in the boundary relations for the conormal
derivative of this potential (see [2, ch. V, § 2], [3, ch. IV, § 15], [4, 5]).
Using a f.s. ![]() we can identify
and explore in the unbounded
domain the properties of two integrals connected with the operator
we can identify
and explore in the unbounded
domain the properties of two integrals connected with the operator ![]()
![]()
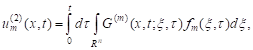 | (4) |
| (5) |
The first integral is called the volumetric
potential and the second one is called the Poisson potential. If specified
functions ![]()
![]()
![]() and
and ![]()
![]()
![]() are bounded and
continuous,
are bounded and
continuous, ![]() satisfies the Holder condition for variable
satisfies the Holder condition for variable ![]() uniformly
relative to
uniformly
relative to ![]() then the function
then the function ![]() satisfies the equation
satisfies the equation
| (6) |
in the
domain ![]() with a zero initial condition
with a zero initial condition ![]()
![]() and the
function
and the
function ![]() satisfies equation (1)
in the same domain with the initial condition
satisfies equation (1)
in the same domain with the initial condition
| (7) |
Considering this, we can give the general
classical solution of the Cauchy problem
(6), (7) as the sum of potentials (4), (5). And
if ![]()
![]() then the potentials (4),
(5) and therefore
the solution of the prob-
lem (6), (7) belongs to the Holder class
then the potentials (4),
(5) and therefore
the solution of the prob-
lem (6), (7) belongs to the Holder class ![]()
We will consider the following conjugation
problem: we have to find the function ![]()
![]()
![]() based on the
conditions
based on the
conditions
| (8) |
| (9) |
| (10) |
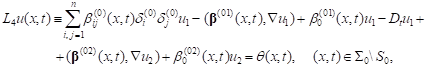 | (11) |
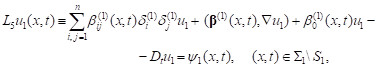 | (12) |
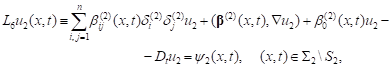 | (13) |
where ![]()
![]()
![]()
We assume
that for the coefficients of the Wentzel type operators ![]()
![]() and
and ![]() the
following conditions hold:
the
following conditions hold:
| (В1) |
| (В2)
|
Also we assume, that
| (14) |
| (15) |
We will assume that for the function ![]()
![]()
![]()
![]()
![]()
![]() from
(8)-(13) the agreement conditions hold at
from
(8)-(13) the agreement conditions hold at ![]() and
these conditions are determined by
a given the boundary conditions (12), (13) and the conjugation condition (11).
and
these conditions are determined by
a given the boundary conditions (12), (13) and the conjugation condition (11).
Then the following statement is true.
Theorem. Let for the coefficients of the
operators ![]()
![]() and
and ![]()
![]()
![]() conditions (А1), (А2) and
(В1), (В2) hold, respectively, for the surfaces
conditions (А1), (А2) and
(В1), (В2) hold, respectively, for the surfaces ![]()
![]() and
the functions
and
the functions ![]()
![]()
![]()
![]()
![]()
![]() from
the right-hand side (8)-(13) the conditions (14) and (15) hold. Then the
problem (8)-(13) has a unique solution
from
the right-hand side (8)-(13) the conditions (14) and (15) hold. Then the
problem (8)-(13) has a unique solution
| (16) |
in the performance the appropriate agreement conditions and the estimation
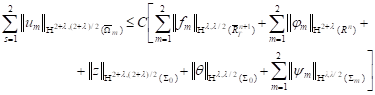 | (17) |
is true.
Proof. We will look for the solution of the problem (8)-(13) in the form
| (18) |
of the sum of the simple-layer potentials (2), (3) with the unknown densities ![]()
![]() and the potentials (4), (5) with the known functions
and the potentials (4), (5) with the known functions ![]()
![]() Using the properties of these potentials, we will find the unknown
functions
Using the properties of these potentials, we will find the unknown
functions ![]() and
and ![]()
![]() so that for
so that for ![]()
![]() the conditions (10)-(13) have been met.
the conditions (10)-(13) have been met.
Let us consider a priori that unknown
densities ![]() and
and ![]()
![]() satisfy the conditions
satisfy the conditions
| (19) |
Now we pass to investigating the conjugation condition by Wentzel type (11). First, we transform this equality by separating its tangential and conormal components in the expressions that contain the derivatives of the first order in space variables using ratio
| (20) |
where ![]()
![]()
![]() is a
tangent differential operator on
is a
tangent differential operator on ![]()
![]()
![]()
Then using (20) and the relationship from the theorem on the jump of the conormal derivative from the simple-layer potential (see [4]), we can write the condition (11) as
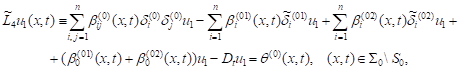 | (21) |
where
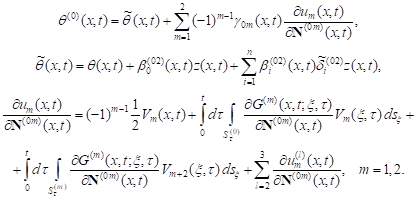 | (22) |
For the kernel ![]()
![]() in the first and second integral from (22)
the estimations (
in the first and second integral from (22)
the estimations (![]()
![]() )
)
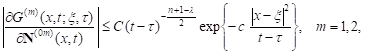 | (23) |
are true.
Now, consider (21) as the autonomic parabolic
equation on ![]() for the function
for the function ![]() For its solution we introduce the
following transformation of the variables:
For its solution we introduce the
following transformation of the variables:
The conjugation condition (21) in new variables will take the form:
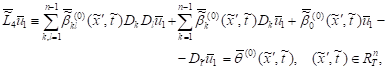 | (24) |
where
|
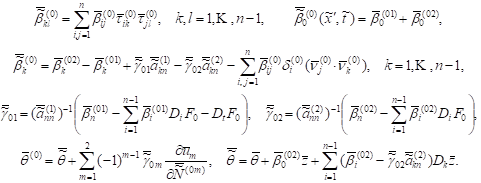
If follows from the conditions of Theorem,
the additional assumption (19), formulae (25) and properties of the potentials
that the coefficients and the function on the right-hand side of this equation
belong to the space ![]() It is known that, the unique
solution
It is known that, the unique
solution ![]() of the equation (24) which satisfies
the initial condition
of the equation (24) which satisfies
the initial condition ![]()
![]() can
be represented by the formula
can
be represented by the formula
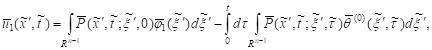 | (26) |
where ![]() (
(![]()
![]() ) is a f.s. of the uniformly para-
bolic equation
) is a f.s. of the uniformly para-
bolic equation ![]() Returning to the variables
Returning to the variables ![]() we can write equality (26) as
we can write equality (26) as
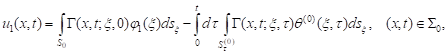 | (27) |
where ![]()
![]()
![]()
![]() The function
The function ![]()
![]() belongs
to class
belongs
to class ![]() as well.
as well.
Thus, we have two representations for values
of function ![]() on
on ![]() relation (18), where one should put
relation (18), where one should put ![]()
![]() and relation
(27). Then, comparing the right-hand sides of equalities (18) and (27) and
taking into account (25), we obtain the first integral equation for the unknown
functions
and relation
(27). Then, comparing the right-hand sides of equalities (18) and (27) and
taking into account (25), we obtain the first integral equation for the unknown
functions ![]() and
and ![]()
![]() Using the
equality (27) and the conjugation condition (10), we find the second equation
for these functions. The third and fourth equations of the required system for
Using the
equality (27) and the conjugation condition (10), we find the second equation
for these functions. The third and fourth equations of the required system for ![]() and
and ![]()
![]() we obtain from
the boundary conditions (12) and (13) similar to the way in which we found the
first equation. After appropriate transformations, an obtained system of four
equations for the unknown functions
we obtain from
the boundary conditions (12) and (13) similar to the way in which we found the
first equation. After appropriate transformations, an obtained system of four
equations for the unknown functions ![]() and
and ![]()
![]() can be represented as
can be represented as
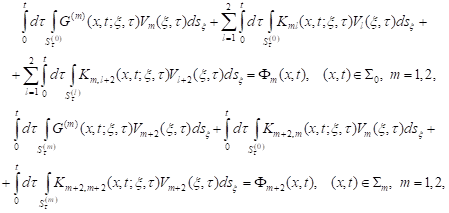 | (28) |
where
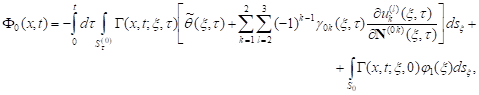 |
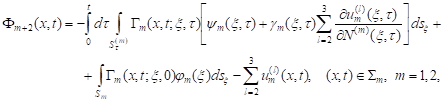 |
![]() and
and ![]() are the f.s. of the parabolic equations
which we obtained after transformation of the boundary conditions (12) and (13)
using the scheme to obtain
the equation (21). The kernels
are the f.s. of the parabolic equations
which we obtained after transformation of the boundary conditions (12) and (13)
using the scheme to obtain
the equation (21). The kernels ![]()
![]()
![]()
![]()
![]()
![]() are expressed by the functions which
have a „weaker” singularity than the function
are expressed by the functions which
have a „weaker” singularity than the function ![]() at
at ![]()
So, we have a system of four integral
Volterra equations of the first kind (28) for ![]() and
and ![]()
![]() The functions
The functions ![]()
![]()
![]() and
and ![]()
![]()
![]() from right-hand side of equations of this system belong to the Holder classes
from right-hand side of equations of this system belong to the Holder classes ![]() and
and ![]() respectively.
In order to transform each of the equations of this
system, we introduce the special integro-differential operators similar to the
operator that was introduced (see [4, 8, 13-16]) in the study of the first
boundary-value parabolic problem by the boundary integral equation method.
respectively.
In order to transform each of the equations of this
system, we introduce the special integro-differential operators similar to the
operator that was introduced (see [4, 8, 13-16]) in the study of the first
boundary-value parabolic problem by the boundary integral equation method.
Let ![]() In
this case, the integro-differential operators (denote them by
In
this case, the integro-differential operators (denote them by ![]()
![]() ) which will be used to transform the first two equations of system
(28), can be defined by the formula
) which will be used to transform the first two equations of system
(28), can be defined by the formula
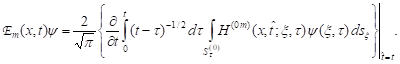 | (29) |
Here the function ![]() (
(![]()
![]()
![]() ),
), ![]() is a f.s. of
the uniformly parabolic operator, which is a trace of the operator
is a f.s. of
the uniformly parabolic operator, which is a trace of the operator ![]()
![]() on
on ![]() To transform the third and fourth
equations of the system (28), we use the integro-differential operators
To transform the third and fourth
equations of the system (28), we use the integro-differential operators ![]()
![]() which are similar to the operator
which are similar to the operator ![]()
![]() from (29). To this end on the right-hand side (29) we should
replace the function
from (29). To this end on the right-hand side (29) we should
replace the function ![]() and integrate over the surface
and integrate over the surface ![]() to the function
to the function
![]() and
integrate over the surface
and
integrate over the surface ![]() respectively. Here
respectively. Here ![]() (
(![]()
![]()
![]() ) is a f.s. of the parabolic operator, which is a trace of the
operator
) is a f.s. of the parabolic operator, which is a trace of the
operator ![]() on
on ![]()
![]()
Applying ![]() and
and ![]()
![]() to both sides of the corresponding
equations of the system (28), we transform this system into the equivalent system of the integral
Volterra equations of the second kind
to both sides of the corresponding
equations of the system (28), we transform this system into the equivalent system of the integral
Volterra equations of the second kind
|
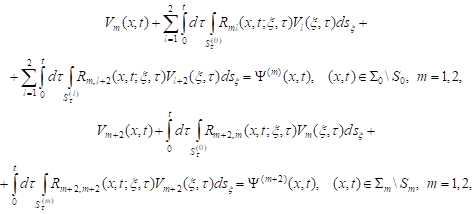
where
And for the kernels ![]()
![]()
![]()
![]()
![]()
![]() the inequality (23) is true.
the inequality (23) is true.
Solving the system of equations (30) by the
method of subsequent approxima-tions, we find ![]()
![]() One can additionally verify that
One can additionally verify that ![]() and
and ![]()
![]() satisfy the condition (19).
satisfy the condition (19).
We obtained the solution of the problem (8)-(13) by formulas (18), (30). To complete the proof of Theorem, we have to only check that this solution satisfies the condition (16) and the estimate (17). We have to also verify the statement of the Theorem on the uniqueness of this solution.
In this regard, we note that the strict proof of these facts practically repeats the similar statements in the papers [13-16]. The theorem is proved.
7. Conclusions
In the article, we investigated the question
of the classic solvability of the parabolic initial-boundary problem with the
boundary conditions and one Wentzel
conjugation condition in the assumption that the boundaries of the domains are
the elementary noncylindrical surfaces of Holder class ![]() The
solution
is obtained by the usual parabolic simple-layer potentials by using the
boundary
integral equation method. The proposed approach can be used to solve a similar
conjugation problem in the noncylindrical domain of the more general type.
The
solution
is obtained by the usual parabolic simple-layer potentials by using the
boundary
integral equation method. The proposed approach can be used to solve a similar
conjugation problem in the noncylindrical domain of the more general type.
References
[1] Pogorzelski W., Etude de la solution fondamentale de l’équation parabolique, Richerce Matem. 1956, 5, 25-57.
[2] Friedman A., Partial Differential Equations of Parabolic Type, Prentice-Hall, Englewood Cliffs 1964, 7.
[3] Ladyzhenskaya O.A., Solonnikov V.A., Ural’tseva N.N., Linear and Quasilinear Equations for Parabolic Type, Nauka, Moskow 1967.
[4] Baderko E.A., Boundary problems for the parabolic equation and boundary integral equations, Differ. Equations. 1992, 28, 1, 17-23.
[5] Kamynin I.I., Application of Pagni parabolic potentials to boundary problems of mathematical physics, I, Differ. Equations 1990, 26, 5, 829-841.
[6] Ivasyshen S.D., Green Matrices of Parabolic Boundary Problem, Vyshcha shkola, Kiev 1990.
[7] Gytarashu N.V., Eydel’man S.D., Parabolic boundary problems, Kyshynev, Shtynitsa 1992.
[8] Cherepova M.F., Solving of the first boundary problem for parabolic equation of the second order in noncylibdrical domain by the potential method, M., Dep. in VINITI 11.01.85, 361-385 Dep.
[9] Dynkin E.B., Markov Processes, Fizmatgiz, Moskow 1963.
[10] Wentzel A.D., On boundary conditions for multidimensional diffusion processes, Probab. Theory Appl. 1959, 4, 2, 172-185.
[11] Apushkinskaya D.E., Nazarov A.I., Initially-boundary problem with limit Ventzel condition for nondivergent parabolic equations, RAN, Algebra and Analysis 1994, 6, 6, 1-29.
[12] Yi Zeng, Yousong Luo, Linear parabolic equations with ventsel initial boundary conditions, Bull. Austral. Math. Soc. 1995, 51, 465-479.
[13] Kopytko B., Tsapovska Zh., The potential method in a parabolic boundary problem with boundary Wentsel condition, Visnyk Lviv Univ., Ser. Mech.-Math. 2000, 56, 106-115.
[14] Kopytko B.I., Tsapovska Zh.Ya., Integral representation of an operator semigroup describing a diffusion in a domain with Wentzel’s boundary condition, Theory of Stochastic Processes 1999, 5(21), 3-4, 105-112.
[15] Kopytko B.I., Mylyo O.Ya., Tsapovska Zh.Ya., A parabolic conjugation problem with general boundary condition and conjugation condition of Wentzel type, Carpatian Mathematical Publications 2010, 2, 2, 55-73.
[16] Kopytko B.I., Tsapovska Zh.Ya.. Initial boundary-value problem with Wentzel-type conjuga-tion condition for a parabolic equation with discontinuous coefficients, Journal of Mathematical Sciences 2009, 160, 3, 283-295.


