Analytical solution of the dual phase lag equation describing the laser heating of thin metal film
Mariusz Ciesielski
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Ciesielski_2017,
doi = {10.17512/jamcm.2017.1.03},
url = {https://doi.org/10.17512/jamcm.2017.1.03},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {1},
pages = {33--40},
author = {Mariusz Ciesielski},
title = {Analytical solution of the dual phase lag equation describing the laser heating of thin metal film},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.1.03 UR - https://doi.org/10.17512/jamcm.2017.1.03 TI - Analytical solution of the dual phase lag equation describing the laser heating of thin metal film T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Ciesielski, Mariusz PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 33 EP - 40 IS - 1 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Ciesielski, M. (2017). Analytical solution of the dual phase lag equation describing the laser heating of thin metal film. Journal of Applied Mathematics and Computational Mechanics, 16(1), 33-40. doi:10.17512/jamcm.2017.1.03
Ciesielski, M., 2017. Analytical solution of the dual phase lag equation describing the laser heating of thin metal film. Journal of Applied Mathematics and Computational Mechanics, 16(1), pp.33-40. Available at: https://doi.org/10.17512/jamcm.2017.1.03
[1]M. Ciesielski, "Analytical solution of the dual phase lag equation describing the laser heating of thin metal film," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 1, pp. 33-40, 2017.
Ciesielski, Mariusz. "Analytical solution of the dual phase lag equation describing the laser heating of thin metal film." Journal of Applied Mathematics and Computational Mechanics 16.1 (2017): 33-40. CrossRef. Web.
1. Ciesielski M. Analytical solution of the dual phase lag equation describing the laser heating of thin metal film. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(1):33-40. Available from: https://doi.org/10.17512/jamcm.2017.1.03
Ciesielski, Mariusz. "Analytical solution of the dual phase lag equation describing the laser heating of thin metal film." Journal of Applied Mathematics and Computational Mechanics 16, no. 1 (2017): 33-40. doi:10.17512/jamcm.2017.1.03
ANALYTICAL SOLUTION OF THE DUAL PHASE LAG EQUATION DESCRIBING THE LASER HEATING OF THIN METAL FILM
Mariusz Ciesielski
Institute of Computer and Information
Sciences, Czestochowa University of Technology
Częstochowa, Poland
mariusz.ciesielski@icis.pcz.pl
Received: 5 January 2017; accepted:
13 March 2017
Abstract. Heat transfer processes occurring in the micro-domains can be described using the dual-phase lag equation (DPLE). This equation can be applied as a model of heating of the thin metal film subjected to the femtosecond laser pulse. In the paper, the 1D dual phase lag equation containing the additional internal heat source resulting from the laser pulse irradiation and supplemented by the appropriate boundary and initial conditions is considered. Appearing in this equation two lag times τq (the phase lag of the heat flux) and τT (the phase lag of the temperature gradient) are taken into account. An analytical solution of this equation under the assumption that τT > τq is presented. The separation of the variables technique and the Green’s function method are used in order to find this solution. In the final part of the paper, the example of computations is presented.
MSC 2010: 65M80, 35L20
Keywords: dual phase lag equation, laser heating process, analytical solution, Green’s function method
1. Introduction
The thermal processes proceeding in the micro-domain of thin metal film subjected to a strong laser pulse are characterized by the extreme temperature gradients, the extremely short duration, and additionally the very small geometrical dimensions. In this case, the application of the classical Fourier heat transfer model is not recommended. The non-Fourier models are proposed as well as the dual phase lag model (DPLM) which is considered in the presented paper. DPLE belongs to the group of the hyperbolic partial differential equations. In this equation, two positive constants τq, τT (the relaxation time and the thermalization time) appear. Nowadays, the problem of heat transfer through the thin metal films subjected to the strong external heat source (e.g. the femtosecond laser pulse) is the subject of many scientific papers [1-8].
In this paper, the considerations concerning the analytical solution of DPLE in the 1D bounded domain are discussed. To obtain this solution, the combination of the variables separation method and the Green’s function is used. The particular solution for the given laser beam profile (as a time dependent function) is presented. In the final part of the paper, the example of computations is shown.
2. Governing equations
The following energy equation corresponding to the DPLM for the domain oriented in the Cartesian co-ordinate system is considered (e.g. [9-11]
| (1) |
where T is a
temperature, c, ρ, λ denote the specific heat, mass
density and thermal conductivity, τq is a relaxation time, while τT is a thermalization time, x, t are the geometrical
co-ordinate and time. The function F is related with the internal heat source ![]() which is generated inside the domain, as the effects of the femto-
second laser pulse irradiation on the metal film
surface (the energy is fed into the domain interior
and its absorption takes place). So
which is generated inside the domain, as the effects of the femto-
second laser pulse irradiation on the metal film
surface (the energy is fed into the domain interior
and its absorption takes place). So
| (2) |
where
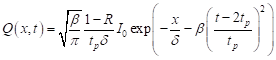 | (3) |
and I0 is a laser intensity, R is a reflectivity of an irradiated surface, δ is an optical penetration depth, β = 4 ln2 and tp is a characteristic time of laser pulse.
On the boundaries of the 1D domain of thickness L, the adiabatic conditions are assumed
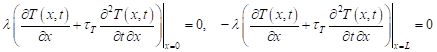 | (4) |
The initial temperature and the initial heating rate are also given
| (5) |
3. Analytical solution
The solution of the 1D hypergeometric partial differential equation (Eq. (1) with the initial conditions (5) and the no-flux boundary conditions (4)) can be found in the general form as [12, 13]
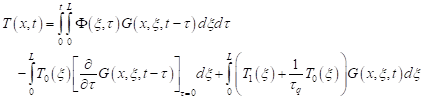 | (6) |
where the Green
function ![]() is determined by solving the
following homogenous equation
is determined by solving the
following homogenous equation
| (7) |
which satisfies the initial conditions
| (8) |
and the homogenous boundary conditions
| (9) |
According to [12], the Green’s function can be expressed as
| (10) |
where functions ![]() and
and ![]() should
be determined. So, the particular solution of Eq. (1) for
should
be determined. So, the particular solution of Eq. (1) for ![]() is the product of the functions
is the product of the functions
| (11) |
Next, introducing Eq.
(11) into Eq. (1) and omitting the term ![]() one obtains the equation
one obtains the equation
| (12) |
After the separation
of variables in above equation, and assuming that both sides
of (12) are equal to the same constant value, i.e. ![]()
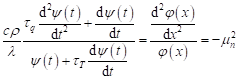 | (13) |
one obtains the following equations
| (14) |
| (15) |
The eigenfunctions and eigenvalues of the Sturm-Liouville problem (14), in which the boundary conditions are determined by the substitution (11) into (4), are the following
| (16) |
and thus
| (17) |
The functions ![]() are
determined by solving Eq. (15) with the initial conditions
are
determined by solving Eq. (15) with the initial conditions ![]() and
and ![]() .
If one assumes that
.
If one assumes that ![]() , then the solution
of the considered initial problem simplifies to the form
, then the solution
of the considered initial problem simplifies to the form
| (18) |
where
| (19) |
Putting Eqs. (16) and (18) into Eq. (10), one finally obtains the Green’s function in the form
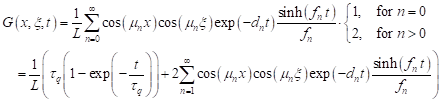 | (20) |
It can be easily checked that the Green’s function (10) satisfies the problem (7)-(9).
The knowledge of the Green’s function and the boundary-initial conditions allows one to use the analytical solution (6) for numerical computations. From a practical point of view, such a form of a solution containing the integrals can be inconvenient. Therefore by using the analytical techniques, the particular terms in Eq. (6) will be simplified. So, the first term (after numerous mathematical transformations) can be written as
| (21) |
where
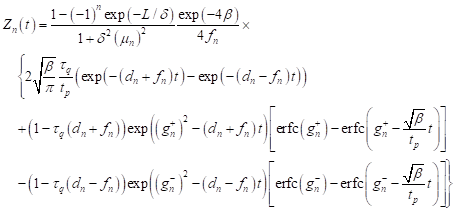 | (22) |
| (23) |
and
| (24) |
It should be pointed out, that the direct computational approach to
the product of the functions ![]() computations, especially for the large arguments, can be inconvenient.
In this place, one can propose using the approximation
methods - see e.g. [14].
computations, especially for the large arguments, can be inconvenient.
In this place, one can propose using the approximation
methods - see e.g. [14].
In the case of ![]() and
and
![]() , the second and third terms in Eq. (6)
are reduced to the form
, the second and third terms in Eq. (6)
are reduced to the form
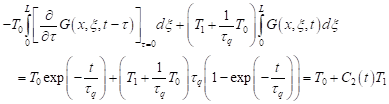 | (25) |
where
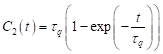 | (26) |
Finally, the analytical solution of the problem (1)-(5) for the constant values appearing in the initial conditions can be written in the form
| (27) |
4. Results of computations
Thermal process proceeding in the thin gold film (L = 100·10–9 m) subjected to the short-pulse laser heating is considered. Thermophysical parameters of the gold are the following: l = 317 W/(mK), c·ρ = 2.4897·106 J/(m3K), tq = 8.5·10–12 s, tT = 90·10–12 s [10]. The parameters of the laser pulse are equal to: I0 = 13.7 W/m2, R = 0.93, d = 15.3·10–12 m, tp = 100·10–15 s. The initial temperature is constant T0 = 20°C and the initial heating rate is equal to T1 = 0 K/s.
In Figure 1, the temperature histories at the
set of selected points in the domain ![]() and the temperature profiles for times
and the temperature profiles for times ![]() are shown.
are shown.


Fig. 1. Temperature histories and temperature profiles
5. Final remarks
The exact analytical solution of the DPLM describing the heat conduction in the 1D domain taking into account the action of the internal heat source is presented. This solution is obtained by combining the methods of variables separation and the Green’s function.
At the stage of mathematical computations, it was assumed that the value of τT is greater than the value of τq (this assumption is quite acceptable in the case of metals). So, the presented solution is only related to the case of τT > τq. In the other cases (the adequate considerations are omitted here), the additional conditions should be taken into account and the solution has a more complicated form. It should be pointed out that the assumption in this solution that τT = 0 (which corresponds to the Cattaneo-Vernotte model) or τT = 0 and τq = 0 (the Fourier model) is not acceptable.
The interesting thing, from a practical point of view, can be the comparison of the results obtained by the different numerical methods used to solve the DPLE with the results of the analytical solution. A disadvantage of the analytical solution proposed is the assumption concerning the constant values of the thermal parameters of the material considered. The numerical solutions allow one, in a simple way, to introduce the temperature-dependent parameters (when the adequate input data data is available).
Acknowledgement
The paper and research are financed within the project 2015/19/B/ST8/01101 sponsored by National Science Centre (Poland).
References
[1] Al-Nimr M.A., Heat transfer mechanism during short duration laser heating in thin metal films, International Journal of Thermophysics 1997, 18(5), 1257-1268.
[2] Tzou D.Y., Chiu K.S., Temperature-dependent thermal lagging in ultrafast laser heating, International Journal of Heat and Mass Transfer 2001, 44, 1725-1734.
[3] Majchrzak E., Mochnacki B., Greer A.L., Suchy J.S., Numerical modeling of short laser pulse interactions with multi-layered thin metal films, Computer Modeling in Engineering and Sciences 2009, 41(2), 131-146.
[4] Majchrzak E, Mochnacki B., Suchy J.S., Numerical simulation of thermal processes proceeding in multi-layered film subjected to ultrafast laser heating, Journal of Theoretical and Applied Mechanics 2009, 47, 2, 383-396.
[5] Belkhayat-Piasecka A., Korczak A., Modeling of transient heat transport in metal films using the interval lattice Boltzmann method, Bulletin of the Polish Academy of Sciences - Technical Sciences 2016, 64(3), 599-505.
[6] Mochnacki B., Ciesielski M., Numerical model of thermal processes in domain of thin film subjected to a cyclic external heat flux, Materials Science Forum 2012, 706-709, 1460-1465.
[7] Majchrzak E., Mochnacki B., Sensitivity analysis of transient temperature field in microdomains with respect to the dual-phase-lag model parameters, International Journal for Multiscale Computational Engineering 2014, 12(1), 65-77.
[8] Majchrzak E., Turchan L., Modeling of phase changes in the metal micro-domains subjected to ultrafast laser heating using dual-phase lag equation, Materialwissenschaft und Werkstofftechnik 2016, 47 (5-6), 409-418.
[9] Tzou D.Y., Macro- to Microscale Heat Transfer. The Lagging Behavior, John Wiley & Sons Ltd, 2015.
[10] Tang D.W., Araki N., Wavy, wavelike, diffusive thermal responses of finite rigid slabs to high-speed heating of laser-pulses, International Journal of Heat and Mass Transfer 1999, 42, 855-860.
[11] Zhang Z.M., Nano/microscale Heat Transfer, McGraw-Hill, New York 2007.
[12] Polyanin A.D., Nazaikinskii V.E., Handbook of Linear Partial Differential Equations for Engineers and Scientists, Second Edition, CRC Press, Boca Raton-London 2016.
[13] Wang L., Zhou X., Wei X., Heat Conduction: Mathematical Models and Analytical Solutions, Springer, Berlin, Heidelberg 2008.
[14] Cody W.J., Rational Chebyshev approximations for the error function, Mathematics of Computation 1969, 23(107), 631-637.


