One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary
Bohdan Kopytko
,Roman Shevchuk
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Kopytko_2016,
doi = {10.17512/jamcm.2016.4.08},
url = {https://doi.org/10.17512/jamcm.2016.4.08},
year = 2016,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {15},
number = {4},
pages = {71--82},
author = {Bohdan Kopytko and Roman Shevchuk},
title = {One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2016.4.08 UR - https://doi.org/10.17512/jamcm.2016.4.08 TI - One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Kopytko, Bohdan AU - Shevchuk, Roman PY - 2016 PB - The Publishing Office of Czestochowa University of Technology SP - 71 EP - 82 IS - 4 VL - 15 SN - 2299-9965 SN - 2353-0588 ER -
Kopytko, B., & Shevchuk, R. (2016). One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary. Journal of Applied Mathematics and Computational Mechanics, 15(4), 71-82. doi:10.17512/jamcm.2016.4.08
Kopytko, B. & Shevchuk, R., 2016. One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary. Journal of Applied Mathematics and Computational Mechanics, 15(4), pp.71-82. Available at: https://doi.org/10.17512/jamcm.2016.4.08
[1]B. Kopytko and R. Shevchuk, "One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 4, pp. 71-82, 2016.
Kopytko, Bohdan, and Roman Shevchuk. "One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary." Journal of Applied Mathematics and Computational Mechanics 15.4 (2016): 71-82. CrossRef. Web.
1. Kopytko B, Shevchuk R. One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(4):71-82. Available from: https://doi.org/10.17512/jamcm.2016.4.08
Kopytko, Bohdan, and Roman Shevchuk. "One-dimensional diffusion processes in half-bounded domains with reflection and a possible jump-like exit from a moving boundary." Journal of Applied Mathematics and Computational Mechanics 15, no. 4 (2016): 71-82. doi:10.17512/jamcm.2016.4.08
ONE-DIMENSIONAL DIFFUSION PROCESSES IN HALF-BOUNDED DOMAINS WITH REFLECTION AND A POSSIBLE JUMP-LIKE EXIT FROM A MOVING BOUNDARY
Bohdan Kopytko 1, Roman Shevchuk 2
1 Institute
of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
2 Vasyl Stefanyk Precarpathian National University
Ivano-Frankivsk, Ukraine
bohdan.kopytko@im.pcz.pl, r.v.shevchuk@gmail.com
Received: 01 August
2016; accepted: 31 August 2016
Abstract. By the method of the classical potential theory, we construct the two-parameter Feller semigroup of operators associated with such a diffusion phenomenon on a half-line with a moving boundary where either a reflection or jump phenomenon occurs at a boundary point.
Keywords: diffusion process, parabolic potential, Feller-Wentzell boundary condition
1. Introduction
In the theory of stochastic processes while studying the diffusion processes in bounded and half-bounded domains, it occurs the situation in which the continuation of motion of a diffusion particle after it reaches the boundary of the domain is performed by jumps. The question on construction of semigroups of operators associated with the diffusion process with the property of a jump-like exit from the boundary of the domain leads to the statement of a boundary-value problem for a linear parabolic equation of the second order with a nonlocal boundary condition. Since the general form of boundary conditions for a one-dimensional (with respect to spatial variable) time-homogeneous diffusion process was established in the works of W. Feller [1] and A.D. Wentzell [2], these conditions were called Feller- -Wentzell boundary conditions.
In the present paper we consider the
one-dimensional parabolic boundary-value problem of Wentzell (with the combination of the derivative with respect
to spatial variable and the nonlocal term) for the case of an inhomogeneous
diffusion process in domain ![]() provided the lateral boundary
provided the lateral boundary ![]() satisfies the Hölder condition
with respect to the time variable with exponent >
satisfies the Hölder condition
with respect to the time variable with exponent > ![]() . This problem is stated
in Section 2 and is solved there by the method of ordinary parabolic
potentials. Using its solution in Section 3, we construct the two-parameter
semigroup
of operators
. This problem is stated
in Section 2 and is solved there by the method of ordinary parabolic
potentials. Using its solution in Section 3, we construct the two-parameter
semigroup
of operators ![]() (
(![]() fixed), associated with an inhomogeneous Feller process on
the closure
fixed), associated with an inhomogeneous Feller process on
the closure ![]() of
of ![]() which
coincides in
which
coincides in ![]() with
the diffusion process given there and its behaviour at point
with
the diffusion process given there and its behaviour at point ![]() is determined
by the Feller-Wentzell boundary condition.
is determined
by the Feller-Wentzell boundary condition.
Note that similar problems were considered earlier in [3, 4] for the case of bounded and half-bounded domains with fixed boundary points. We also mention works [5-7] where the related problems were studied by the methods of stochastic analysis.
2. Parabolic boundary-value problem of Wentzell
Consider on plane ![]() the set
the set
denoting by ![]() the
closure of
the
closure of ![]() . Let in
. Let in ![]() the
parabolic equation
the
parabolic equation
| (1) |
is given. We shall seek a solution ![]() of equation (1) satisfying the
“initial” condition
of equation (1) satisfying the
“initial” condition
| (2) |
and the Feller-Wentzell boundary condition of the form
| (3) |
(![]() ).
).
The main problem is to find the function ![]() which belongs to
which belongs to ![]() and which satisfies the equation (1) in
and which satisfies the equation (1) in
![]() , the “initial” condition (2) and the
boundary condition (3).
, the “initial” condition (2) and the
boundary condition (3).
In the present paper, the following conditions are supposed to be satisfied:
1. The
coefficients ![]() and
and ![]() are bounded on
are bounded on ![]() ,
besides,
there exist positive constants
,
besides,
there exist positive constants ![]() and
and ![]() such that
such that ![]() for
all
for
all ![]() .
.
2. For
all ![]() the next inequalities hold:
the next inequalities hold:
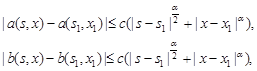
where ![]() and
and ![]() are
positive constants,
are
positive constants, ![]() .
.
3. The
curve ![]() is Hölder
continuous with exponent
is Hölder
continuous with exponent ![]() on
on ![]() .
.
4. ![]() , where
, where ![]() denotes
the Banach space of bounded continuous functions on
denotes
the Banach space of bounded continuous functions on ![]() with
norm
with
norm ![]() .
.
5. The
function ![]() is positive and continuous on
is positive and continuous on ![]() .
.
6. ![]() is the nonnegative measure on
is the nonnegative measure on ![]() such that for any
such that for any ![]()
![]() ,
, ![]() ,
,
where ![]() and these integrals are continuous on
and these integrals are continuous on ![]() as functions of
as functions of ![]()
Denote by ![]() the
fundamental solution of equation (1) (
the
fundamental solution of equation (1) (![]()
![]()
![]() ).
Its existence is assured by 1), 2) (see [5, Ch. II, §2], [8, Ch. IV, §11]).
Recall that function
).
Its existence is assured by 1), 2) (see [5, Ch. II, §2], [8, Ch. IV, §11]).
Recall that function ![]() is nonnegative, jointly
continuous, continuously
differentiable with respect to
is nonnegative, jointly
continuous, continuously
differentiable with respect to ![]() twice continuously differentiable with
respect
to
twice continuously differentiable with
respect
to ![]() and satisfies
the inequality
and satisfies
the inequality
| (4) |
for all ![]()
![]() , where
, where ![]() and
and ![]() are the nonnegative integers such that
are the nonnegative integers such that ![]() ;
; ![]() is
the partial derivative with respect to
is
the partial derivative with respect to ![]() of
order
of
order ![]() ,
, ![]() is
the partial derivative with respect to
is
the partial derivative with respect to ![]() of
order
of
order ![]() ; symbols
; symbols ![]() and
and ![]() denotes (here and in what follows) any
one of various different positive constants.
denotes (here and in what follows) any
one of various different positive constants.
Recall also that
| (5) |
where
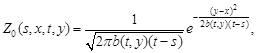 |
and the function ![]() satisfies
inequality
satisfies
inequality
| (6) |
where ![]()
![]() ,
, ![]() ,
, ![]() is the constant in 2.
is the constant in 2.
Having the fundamental solution ![]() we now define
the parabolic potentials that will be used to solve the problem (1)-(3), namely
the Poisson potential
we now define
the parabolic potentials that will be used to solve the problem (1)-(3), namely
the Poisson potential
![]()
where ![]() is the function in
(2), and the simple-layer potential
is the function in
(2), and the simple-layer potential
![]()
with density ![]() which
is continuous in
which
is continuous in ![]() and satisfies the inequality
and satisfies the inequality
![]()
for any ![]() . The
last inequality ensures the validity of the formula on the jump for potential
. The
last inequality ensures the validity of the formula on the jump for potential ![]() (see [9, Ch. V, §§2-4])
(see [9, Ch. V, §§2-4])
| (7) |
where
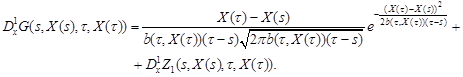
Furthermore, from condition 3 and estimate (6) it follows that
| (8) |
We find the solution of problem (1)-(3) of the form
| (9) |
with the unknown function ![]() to be determined.
to be determined.
If we substitute the expression (9) for ![]() into (3), we obtain, upon using the
relation (7), the following Volterra integral equation of the second kind
into (3), we obtain, upon using the
relation (7), the following Volterra integral equation of the second kind
| (10) |
where
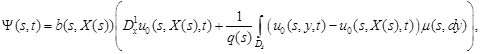
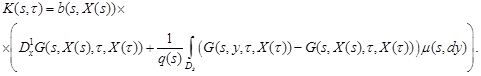
In order to solve this integral equation, we
have to study the behavior of function ![]() and
kernel
and
kernel ![]() . We begin with estimate for
. We begin with estimate for ![]() . Write
. Write ![]() in
the form
in
the form
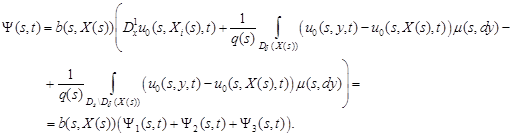
For function ![]() we
have
we
have
| (11) |
To estimate ![]() ,
apply the Lagrange formula to the integrand
,
apply the Lagrange formula to the integrand ![]() in
its expression. We have
in
its expression. We have
![]() ,
,
where ![]() is some real number from interval
is some real number from interval ![]() . Hence
. Hence
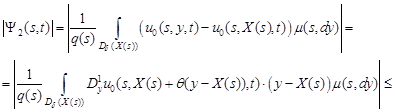
| (12) |
The same estimate is also valid for ![]() . Indeed, using the triangle inequality,
we obtain
. Indeed, using the triangle inequality,
we obtain
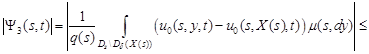
| (13) |
Combining (11), (12) and (13), we conclude that
| (14) |
where ![]() is some positive constant depending on
is some positive constant depending on ![]() .
.
Now consider kernel ![]() .
Write it as follows
.
Write it as follows
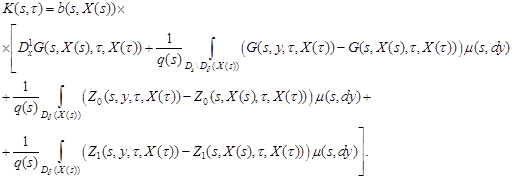
The first term in square brackets in the above expression is already estimated by (8). The absolute values of the second and fourth terms are bounded, respectively, by
![]() and
and ![]()
which becomes clear, respectively, after using
the inequality (4) with
![]() and after applying the Lagrange formula
to difference
and after applying the Lagrange formula
to difference ![]() and using the inequality (6)
with
and using the inequality (6)
with ![]() , successively.
, successively.
It remains to estimate the third term in the
expression for ![]() which we
denote by
which we
denote by ![]() . Write it in the form
. Write it in the form
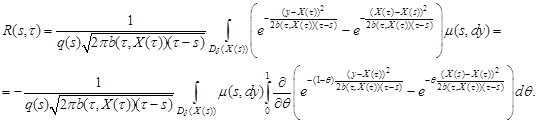
Taking the derivative
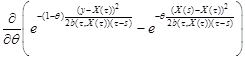 and then using
the equality
and then using
the equality ![]() , we
get
, we
get
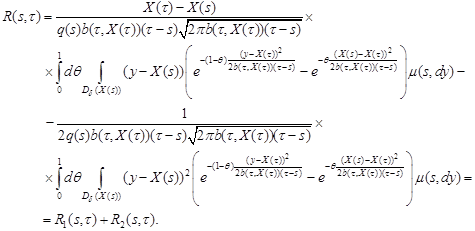
From condition 3 it follows that
![]()
Consider ![]() . Since
. Since
![]()
we have
![]()
![]()
Thus kernel ![]() in (9) has strong singularity which is caused by
in (9) has strong singularity which is caused by ![]() . Therefore we do not know yet
whether a solution of (10) exists. We
shall see
presently that it is nevertheless possible to obtain the solution of (10) by an ordinary method of successive approximations, i.e.,
. Therefore we do not know yet
whether a solution of (10) exists. We
shall see
presently that it is nevertheless possible to obtain the solution of (10) by an ordinary method of successive approximations, i.e.,
| (15) |
where
![]()
![]()
Let us
prove that the integrals on the right side of expression for ![]() exist and the series (15) is convergent in
exist and the series (15) is convergent in ![]() . To
do this, we first break
the expression for
. To
do this, we first break
the expression for ![]() into two terms
into two terms ![]() satisfying the estimate (8) with some positive constant
satisfying the estimate (8) with some positive constant ![]() and
and ![]() having
strong singularity, i.e.,
having
strong singularity, i.e.,
| (16) |
Next, consider ![]() and
represent it as follows
and
represent it as follows
![]()
where
![]()
In view of estimate (8) (with constant ![]() ) for
) for ![]() and
inequality (14), we immediately deduce that
and
inequality (14), we immediately deduce that
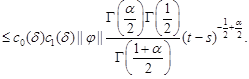 | (17) |
To estimate ![]() ,
write
,
write
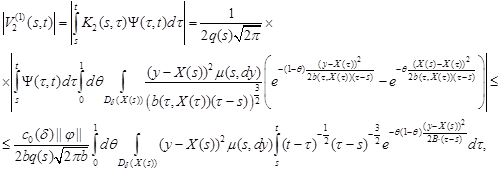
where ![]() and
and ![]() are constants in 1.
are constants in 1.
Denote by ![]() the
inner integral in the last relation. Write it in the form
the
inner integral in the last relation. Write it in the form
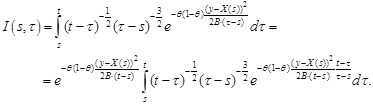
Changing the variable of integration ![]() into
into ![]() , we
obtain
, we
obtain
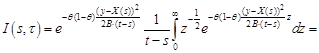
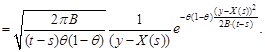 | (18) |
In view of (18), we get
| (19) |
where
Combining (17) and (19), we conclude that
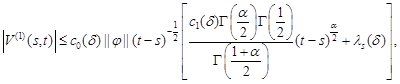 |
Choose ![]() so
small that
so
small that ![]() and denote
and denote
![]()
Proceeding by induction, we derive the
following estimates for terms ![]() of series (15)
of series (15)
| (20) |
where
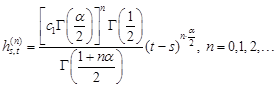
Hence, for ![]() , we
have
, we
have
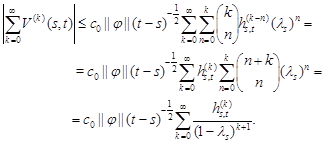
This implies that series (15) is absolutely
convergent in ![]() and therefore the function
and therefore the function ![]() exists and satisfies the inequality
exists and satisfies the inequality
| (21) |
We have thus
constructed a solution ![]() of the boundary-value problem
(1)-(3) of the form (9). From relations (4)-(6) and (21) it follows that
of the boundary-value problem
(1)-(3) of the form (9). From relations (4)-(6) and (21) it follows that
![]()
and
| (22) |
The proof of uniqueness of solution of (1)-(3) is based on the maximum principle for parabolic equations and is a repetition of the proof of the analogous assertion in [3] with obvious changes.
We have proved the following theorem:
Theorem 1. Let
the conditions 1-6 hold. Then the problem (1)-(3) has a
unique
solution ![]() in
in ![]() .
Furthermore, this solution has the form (9) and satisfies the estimate (22).
.
Furthermore, this solution has the form (9) and satisfies the estimate (22).
3. Construction of the Feller semigroup
Consider the following problem: construct the
two-parameter semigroup of
operators ![]() which describes the inhomogeneous Feller process
on
which describes the inhomogeneous Feller process
on ![]() connected with (1)-(3). Such a Feller
process coincides in
connected with (1)-(3). Such a Feller
process coincides in ![]() with the diffusion process
given by (1), (2) (with drift
with the diffusion process
given by (1), (2) (with drift ![]() and diffusion
coefficient
and diffusion
coefficient ![]() ) and its behavior at boundary point
) and its behavior at boundary point ![]() is determined by
the Feller-Wentzell boundary condition (3). Note that the two terms of boundary
condition (3)
is determined by
the Feller-Wentzell boundary condition (3). Note that the two terms of boundary
condition (3)
![]() and
and ![]()
are supposed to correspond to the reflection
phenomenon and the jump phenomenon on the boundary ![]()
We introduce the two-parameter family of
linear operators ![]() acting on the space
acting on the space ![]() by the rule
by the rule
| (23) |
where ![]() is the solution of
problem (1)-(3) defined by formulas (9), (15).
is the solution of
problem (1)-(3) defined by formulas (9), (15).
Let us
show that the family of operators ![]() is the desired semigroup. To do this, we first note that the
operators
is the desired semigroup. To do this, we first note that the
operators ![]() have the following property: if the se-
quence
have the following property: if the se-
quence ![]() is such that
is such that ![]() for all
for all ![]() and
and ![]() then
then
![]() for all
for all ![]() The proof of this property is based on well-known assertions of
calculus on the passage of the limit under the summation and integral signs
(here this concerns series (15) and integrals on the right side of the
expression (9)). This property allows us to prove the next properties of the
operator family
The proof of this property is based on well-known assertions of
calculus on the passage of the limit under the summation and integral signs
(here this concerns series (15) and integrals on the right side of the
expression (9)). This property allows us to prove the next properties of the
operator family ![]() , without loss of generality, under the assumption that the function
, without loss of generality, under the assumption that the function ![]() has a compact support.
has a compact support.
The next lemma asserts that the operators ![]() are positivity
preserving:
are positivity
preserving:
Lemma 1. If ![]() and
and ![]() for all
for all ![]() ,
then
,
then ![]() for all
for all ![]()
Proof. Let ![]() be any nonnegative function in
be any nonnegative function in ![]() having compact support.
Denote by
having compact support.
Denote by ![]() the minimum of
the minimum of ![]() in
in ![]() and
assume that
and
assume that ![]() . From the minimum principle it follows
that there exists
. From the minimum principle it follows
that there exists ![]() such that
such that ![]() . But then the inequalities
. But then the inequalities
![]() and
and ![]()
hold. Furthermore, Theorem 14 in [9, p. 69] assures us that
![]()
Next, since ![]() it
becomes clear that the fulfillment of condition (3) is
impossible. The contradiction we arrived at indicates that
it
becomes clear that the fulfillment of condition (3) is
impossible. The contradiction we arrived at indicates that ![]() This completes
the proof of the lemma.
This completes
the proof of the lemma. ![]()
Another
important property of operators ![]() is that they are contractive,
i.e.,
is that they are contractive,
i.e.,
![]()
This property follows from Lemma 1 together with
the fact that if ![]() 1 then
1 then ![]() for
all
for
all ![]() .
.
Finally, we show that operator family ![]() has the semigroup property
has the semigroup property
![]()
This property is a consequence of the assertion
of uniqueness of the solution
of the problem (1)-(3). Indeed, to
find ![]() when
when ![]() , we can solve the problem (1)-(3) first in the time interval
, we can solve the problem (1)-(3) first in the time interval
![]() with the “initial” function
with the “initial” function ![]() , and then in the time interval
, and then in the time interval ![]() with the “initial” function
with the “initial” function ![]() .
In other words,
.
In other words, ![]()
![]() or
or ![]()
The above properties of operators ![]() imply the following assertion (see [10, Ch. II], §1):
imply the following assertion (see [10, Ch. II], §1):
Theorem 2. Let
the conditions of Theorem 1 hold. Then the two parameter semigroup of operators ![]() defined by (23) describes the inhomoge-
neous Feller process on
defined by (23) describes the inhomoge-
neous Feller process on ![]() which coincides in
which coincides in ![]() with
the diffusion process given by (1),
(2) and its behavior at point
with
the diffusion process given by (1),
(2) and its behavior at point ![]() is determined by the Feller-Wentzell boundary
condition (3).
is determined by the Feller-Wentzell boundary
condition (3).
References
[1] Feller W., The parabolic differential equations and associated semi-groups of transformations, Ann. Math. 1952, 55, 468-518.
[2] Wentzell A.D., Semigroups of operators that correspond to a generalized differential operator of second order, Dokl. AN SSSR 1956, 111(2), 269-272 (in Russian).
[3] Shevchuk R.V., Inhomogeneous diffusion processes on a half-line, generated by the differential operator with Feller-Wentzell boundary condition, Math. Bull. NTSH 2011, 8, 243-257 (in Ukrainian).
[4] Kopytko B.I., Shevchuk R.V., Diffusions in one-dimensional bounded domains with reflection, absorption and jumps at the boundary and at some interior point, Journal of Applied Mathematics and Computational Mechanics 2013, 12(1), 55-68.
[5] Portenko M.I., Diffusion Processes in Media with Membranes, Institute of Mathematics of the NAS of Ukraine, Kyiv 1995 (in Ukrainian).
[6] Pilipenko A.Yu., On the Skorokhod mapping for equations with reflection and possible jump-like exit from a boundary, Ukrainian Math. J. 2012, 63(9), 1415-1432.
[7] Anulova S.V., On stochastic differential equations with boundary conditions in a half-plane, Izv. AN SSSR Ser. Mat. 1981, 45(3), 491-508 (in Russian).
[8] Ladyzhenskaya O.A., Solonnikov V.A., Ural’tseva N.N., Linear and Quasilinear Equations of Parabolic Type, Nauka, Moscow 1967 (in Russian).
[9] Friedman A., Partial Differential Equations of Parabolic Type, Mir, Moscow 1968 (in Russian).
[10] Dynkin E.B., Markov Processes, Fizmatgiz, Moscow 1963 (in Russian).


