Representations of (D,O)-species and flat mixed matrix problems
Nadiya Gubareni
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Gubareni_2016,
doi = {10.17512/jamcm.2016.3.05},
url = {https://doi.org/10.17512/jamcm.2016.3.05},
year = 2016,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {15},
number = {3},
pages = {47--56},
author = {Nadiya Gubareni},
title = {Representations of (D,O)-species and flat mixed matrix problems},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2016.3.05 UR - https://doi.org/10.17512/jamcm.2016.3.05 TI - Representations of (D,O)-species and flat mixed matrix problems T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Gubareni, Nadiya PY - 2016 PB - The Publishing Office of Czestochowa University of Technology SP - 47 EP - 56 IS - 3 VL - 15 SN - 2299-9965 SN - 2353-0588 ER -
Gubareni, N. (2016). Representations of (D,O)-species and flat mixed matrix problems. Journal of Applied Mathematics and Computational Mechanics, 15(3), 47-56. doi:10.17512/jamcm.2016.3.05
Gubareni, N., 2016. Representations of (D,O)-species and flat mixed matrix problems. Journal of Applied Mathematics and Computational Mechanics, 15(3), pp.47-56. Available at: https://doi.org/10.17512/jamcm.2016.3.05
[1]N. Gubareni, "Representations of (D,O)-species and flat mixed matrix problems," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 3, pp. 47-56, 2016.
Gubareni, Nadiya. "Representations of (D,O)-species and flat mixed matrix problems." Journal of Applied Mathematics and Computational Mechanics 15.3 (2016): 47-56. CrossRef. Web.
1. Gubareni N. Representations of (D,O)-species and flat mixed matrix problems. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(3):47-56. Available from: https://doi.org/10.17512/jamcm.2016.3.05
Gubareni, Nadiya. "Representations of (D,O)-species and flat mixed matrix problems." Journal of Applied Mathematics and Computational Mechanics 15, no. 3 (2016): 47-56. doi:10.17512/jamcm.2016.3.05
REPRESENTATIONS OF (D,O)-SPECIES and FLAT MIXED MATRIX PROBLEMS
Nadiya Gubareni
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
nadiya.gubareni@yahoo.com
Abstract. The problem of describing representations of (D,O)-species is reduced to flat mixed matrix problems over discrete valuation rings and their common skew field of fractions.
Keywords: O-species, (D,O)-species, representations of (D,O)-species, (D,O)-species of bounded representation type, flat mixed matrix problem, discrete valuation ring
1. Introduction
We continue the study of (D,O)-species that was started in [1]. These species generalize the notion of species introduced by Gabriel [2] and are the special kind of species considered in [3].
Let {Oi} be a family of
discrete valuation rings (not necessarily commutative) with a common skew field of fractions D. Consider a (D,O)-species W = (Fi, iMj)i,j Î I , where Fi = ![]() for i = 1, 2, ..., k, and Fj = D for j = k +1, ..., n,
moreover iMj
is an (
for i = 1, 2, ..., k, and Fj = D for j = k +1, ..., n,
moreover iMj
is an (![]() ,
,![]() )-bimodule that is finite dimensional
both as the left D-vector
space and as the right D-vector space, where
)-bimodule that is finite dimensional
both as the left D-vector
space and as the right D-vector space, where ![]() is a
classical ring of fractions of Fi for
i = 1, 2, ..., n.
is a
classical ring of fractions of Fi for
i = 1, 2, ..., n.
A (D,O)-species W is called weak if Fi = Oi for all i = 1, 2, ..., k, and moreover, iMj = 0 if Fj = Oj, and iMj = jMi = 0 for i,j ÎI and i ¹ j.
For (D,O)-species the representations of O-species were defined in [1]. A representation V = (Mi, Vr, jji, jyr) of a weak (D,O)-species W = {Fi, iMj}i,jÎI is a family of right Fi-modules Mi (i = 1, 2, ..., k), a set of right D-vector spaces Vr (r = k +1, k +1, ..., n) and D-linear maps:
for each i = 1, 2, ..., k; j = k +1, k +2, ..., n; and
for each r, j = k +1, k +2, ..., n.
A representation V is said to be finite dimensional if all Mi are finitely generated Fi-modules and all Vr are finite dimensional D-vector spaces. A (D,O)-species is of bounded representation type if the dimensions (see (3.13) in [1]) of its indecomposable finite dimensional representations have an upper bound.
In this paper, we show that the description of representations of (D,O)-species can be reduced to some flat mixed matrix problems over discrete valuation rings and their common skew field of fractions. The definition of such matrix problems is given in Section 2. These matrix problems are some sort of generalization of a flat matrix problem considered by Zavadskii and Revitskaya [4]. Earlier such matrix problems were considered by Gubareni [5, 6], and Zavadskii and Kirichenko [7, 8]. Some examples of such flat matrix problems were also considered in [9]. The reduction of the problem of description of (D,O)-species of bounded representation type to some flat mixed matrix problems is given in Section 3.
With each weak (D,O)-species W = (Fi, iMj)i,jÎI we can associate a D-species ![]() , where
, where ![]() In Section 4, we prove that if W is a simply con-
nected weak (D,O)-species of bounded
representation type, then
In Section 4, we prove that if W is a simply con-
nected weak (D,O)-species of bounded
representation type, then ![]() is a D-species
of finite representation type.
is a D-species
of finite representation type.
2. Flat mixed matrix problems
Let O be a discrete valuation ring (DVR) with a classical division ring of fractions D. By left O-elementary transformations of rows of a matrix T with entries in D we mean transformations of two types:
a) multiplying a row on the left by an invertible element of O;
b) adding a row multiplied on the left by an element of O to another row.
In a similar way we can define left D-elementary transformations of rows and, by symmetry, right O-elementary and right D-elementary transformations of columns.
Elementary transformations (a) and (b) can be given by invertible elementary matrices. The automorphism of a finitely generated module P corresponding to an elementary transformation is an elementary automorphism. Multiplications on the left (right) side of a matrix T by elementary matrices correspond to elementary row (column) transformations.
By [10, Proposition 13.1.3], any invertible matrix B over a local ring O can be reduced by O-elementary row (column) transformations on B to the identity matrix. By [10, Corollary 13.1.4], the matrix B can be decomposed into a product of elemen- tary matrices. Moreover, by [10, Theorem 13.1.6] any automorphism of a finitely generated projective module P over a semiperfect ring A can be decomposed into a product of elementary automorphisms.
Let D = {Oi}{i =1, …, k} be a family of discrete valuation rings Oi with a common skew field of fractions D. We define the general flat matrix problem over D and D in the following way.
Let
|
T11 |
… |
T1j |
… |
T1m |
|
… |
… |
… |
… |
… |
|
Ti1 |
… |
Tij |
… |
T1m |
|
… |
… |
… |
… |
… |
|
Tn1 |
… |
Tnj |
… |
Tnm |
be a block rectangular matrix T with entries in D partitioned into n horizontal strips T1, …, Tn and m vertical strips T1, …, Tm so that each block Tij is the intersection of the j-th vertical strip and the i-th horizontal strip; some of these blocks may be empty.
Assume that the ring ![]() Î D È D
corresponds to the i-th horizontal strip Ti and the ring
Î D È D
corresponds to the i-th horizontal strip Ti and the ring ![]() Î D È D
corresponds to the j-th vertical strip Tj.
Î D È D
corresponds to the j-th vertical strip Tj.
The following transformations with the matrix T are admissible:
1. Left ![]() -elementary transformations of rows within the strip Ti.
-elementary transformations of rows within the strip Ti.
2. Right ![]() -elementary transformations of rows within the strip Tj.
-elementary transformations of rows within the strip Tj.
3. Additions of rows in the strip Tj multiplied on the left by elements of FrÎDÈD to rows in the strip Ti.
4. Additions of columns in the strip Ti multiplied on the right by elements of FpÎDÈD to columns in the strip Tj.
Indecomposable matrices and equivalent matrices are defined in a natural way.
A flat matrix problem is said to be of finite type if the number non-equivalent indecomposable matrices is finite.
Definition 2.1. The vector
| d = d(T) = (d1,d2, … , dn; d1, d2, …, dm), | (2.2) |
where di is the number of rows of the i-th horizontal strip of T for i = 1, ..., n and d j is the number of columns of the j-th vertical strip of T for j = 1, ..., m, is called the dimension vector of the partition matrix T. Also set
| dim(T) = | (2.3) |
Definition 2.4.
A flat matrix problem is said to be of bounded representation type if there is a constant C such that dim(X) < C for all indecomposable matrices X. Otherwise it is of unbounded representation type.
3. The main matrix problem
Let W = (Fi, iMj)i,j Î I, where Fi = Oi for i = 1,2, …, k and Fj = D for j = k+1, …, n, be a weak (D,O)-species of bounded representation type.
Suppose that V = (Mi, Vr, jji, jyr) is an indecomposable finite dimensional representation of W. Then Mi is a finitely generated Fi-module for i =1,2, …, k and Vr is a finite dimensional D-vector space for r = k +1, …, n. Since Fi = Oi is a discrete valuation ring, by [3, Proposition 5.4.18], any Oi-module Mi is torsion-free and faithful. Therefore any indecomposable representation of W has the following form:
| V = (Mi, Vr, jji, jyr) | (3.1) |
where Mi is a free Fi-module.
Consider the
category R(W) whose objects
are representations V = (Mi, Vr, jji, jyr), and a morphism from an
object V to an object ![]() is a set of homo-
morphisms (ai, br), in which
is a set of homo-
morphisms (ai, br), in which ![]() is a
homomorphism of Fi -modules,
is a
homomorphism of Fi -modules, ![]() is a homomorphism of D-vector
spaces (r = k +1, …, n), and
the following equalities hold:
is a homomorphism of D-vector
spaces (r = k +1, …, n), and
the following equalities hold:
| (3.2) |
| (3.3) |
Let V be an indecomposable finite
dimensional representation of the
(D,O)-species W. Thus, each Mi is
a finitely generated free Oi -module with basis ![]() (i = 1,2,
…, k); and Vr is
a finite dimensional D-space with basis
(i = 1,2,
…, k); and Vr is
a finite dimensional D-space with basis ![]() (r
= k +1, …, n).
(r
= k +1, …, n).
Suppose
| (3.4) |
| (3.5) |
Then the matrices Aij = (![]() ), Bij = (
), Bij = (![]() ) define the representation V
uniquely up to equivalence.
) define the representation V
uniquely up to equivalence.
Let Ui Î ![]() be the matrix corresponding to the homomorphism ai, and let Wi Î
be the matrix corresponding to the homomorphism ai, and let Wi Î ![]() be the matrices corresponding to the
homomorphisms bi , i Î I.
If
be the matrices corresponding to the
homomorphisms bi , i Î I.
If ![]() ,
, ![]() are the matrices corresponding to
a representation V ¢ then the
equalities (3.2) and (3.3) have the following matrix form:
are the matrices corresponding to
a representation V ¢ then the
equalities (3.2) and (3.3) have the following matrix form:
| Wi Bij = | (3.6) |
| Wj Ajr = | (3.7) |
If representations V and V ¢ are equivalent, then ai, br are isomorphisms. Therefore, the matrices Ui and Wr are invertible and the equalities (3.2) and (3.3) are equivalent to the following equalities:
| Wi
Bij | (3.8) |
| Wj Ajr | (3.9) |
Thus we obtain the following matrix problem for description of indecomposable finite dimensional representations of a (D,O)-species W.
Main mixed matrix problem
Let D = {Oi}i=1,2,…,k be a family of discrete valuation rings Oi with a common skew field of fractions D.
Let T be a block matrix with entries in D partitioned into n horizontal strips {Ti}{i=1,…,n} and m vertical strips {Tj}{j=1,…,m} so that each block Tij is the intersection of j-th vertical strip and i-th horizontal strip, some of these matrices may be empty.
The following transformations with the matrix T are admissible:
1. Left ![]() -elementary transformations of rows within the strip Ti, where
-elementary transformations of rows within the strip Ti, where ![]()
2. Right ![]() -elementary transformations of rows within
the strip Tj, where
-elementary transformations of rows within
the strip Tj, where ![]()
The admissible transformations with the
matrix T can be given in the form
T ® XTY, where X = diag (X1, …, Xn) and Y = diag (Y1, …, Ym), and all Xi and Yj are square invertible matrices. Moreover, Xi Ì ![]() , and Yj Ì
, and Yj Ì ![]() , where
, where ![]()
Clearly, the matrix T is indecomposable if and only if the corresponding representation of W is indecomposable. It is easy to prove the following statement.
Lemma 3.10. A (D,O)-species W is of bounded representation type if and only if the corresponding main matrix problem is of bounded representation type.
4. Weak (D,O)-species of bounded representation type
Let W = (Fi, iMj)i,j Î I be O-species. The quiver G(W) of an O-species W is defined as the directed graph whose vertices are 1, …, n, and there is an arrow from the vertex i to the vertex j if and only if iMj ¹ 0.
An O-species W is called acyclic if its quiver has no oriented cycles, i.e. the indices can be chosen so that iMi = 0 for all i, and iMj = 0 for j £ i.
A vertex i Î I is called marked if Fi = ![]() . Let I1 = {1, 2, ..., k}
be the set
of marked vertices of an O-species W. A marked vertex i Î I1 is called minimal
if iMj = jMi = 0 for all j Î I1. An O-species W is called min-marked
if all its marked vertices are minimal.
. Let I1 = {1, 2, ..., k}
be the set
of marked vertices of an O-species W. A marked vertex i Î I1 is called minimal
if iMj = jMi = 0 for all j Î I1. An O-species W is called min-marked
if all its marked vertices are minimal.
An O-species W is simply connected if the underlying graph of G(W) is a tree.
A (D,O)-species W = (Fi, iMj)i,j Î I is said to be weak if W is min-marked and all Fi, are Oi or D.
For each O-species
W = (Fi, iMj)i,j Î I in [1], the tensor algebra T(W) = ![]() , where T0 =
, where T0 = ![]() , Ti+1 =
Ti ÄB M
and M =
, Ti+1 =
Ti ÄB M
and M = ![]() , was constructed.
, was constructed.
Lemma 4.1. Let W = (Fi, iMj)i,j Î I, where all Fi = D, be a simply connected D-species of finite representation type. Then the tensor algebra T(W) is a hereditary Artinian semidistributive ring.
Proof. Since W is a simply connected species, the tensor algebra T(W) is Morita equivalent to the algebra
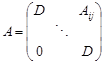 |
where
| Aij = | (4.2) |
Since all iMj are finitely dimensional right and left D-spaces, A is an Artinian ring. From [11, Corollary 2.2.13] it follows that A is a hereditary ring.
Note that the ring
| (4.3) |
where V12 is a (D, D)-bimodule, is of finite representation type if and only if V12 has dimension 1 both as right and as left D-vector space. Since W is a D-species of finite representation type, the tensor algebra T(W) is of finite representation type as well, and so it does not contain a minor that is isomorphic to the ring (4.3). Therefore, A is a semidistributive ring.
Besides
a weak (D,O)-species W = (Fi, iMj)i,j Î I we can also consider a D-species ![]() , where
, where ![]() since each iMj is an (
since each iMj is an (![]() ,
,![]() )-bimodule. Let T(
)-bimodule. Let T(![]() ) be a tensor algebra of D-species
) be a tensor algebra of D-species
![]() . Since T(
. Since T(![]() ) is
an Artinian ring, by [12, 13]
it is of bounded representation type if and only if it is of finite
representation type.
) is
an Artinian ring, by [12, 13]
it is of bounded representation type if and only if it is of finite
representation type.
Proposition 4.4. If
W is a weak simply connected (D,O)-species
of bounded representation type, then ![]() is a D-species of
finite representation type.
is a D-species of
finite representation type.
Proof. Let W be a weak simply connected (D,O)-species with set of marked vertices J = {1,2, ..., k}. Then the tensor algebra A = T(W) is a basic primely triangular ring whose two-sided Peirce decomposition has the following form
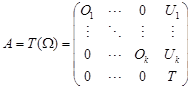 | (4.4) |
where each Ui is a (D,T)-bimodule. Moreover, the ring T is the tensor algebra of a species W1 = (Fi, iMj)i,j Î I \ J, where Fi = D for all i Î I \ J.
Since W is a (D,O)-species of bounded representation type, then the tensor algebra T(W) is also is of bounded representation type by [1, Corollary 3.15]. Then by [1, Corollary 3.16], T is also of bounded representation type. Since W1 is a D-species, T is an Artinian ring and so it is of finite representation type. Since W is simply connected, W1 is also simply connected. By Lemma 4.1, T is an Artinian hereditary semidistributive ring.
Let ![]() be a right
classical ring of fractions of A. We will use the following notation: if
M is a right A-module, then M¢ = M ÄA
be a right
classical ring of fractions of A. We will use the following notation: if
M is a right A-module, then M¢ = M ÄA ![]() ; and if M is a right
; and if M is a right ![]() -module, then M¢ is the
module M considered as an A-module. The length of a composition
series of a right
-module, then M¢ is the
module M considered as an A-module. The length of a composition
series of a right ![]() -module X is denoted by l(X).
-module X is denoted by l(X).
Let us prove that for any right ![]() -module M there is a right
-module M there is a right ![]() -module X such that M¢¢
= M Å X.
-module X such that M¢¢
= M Å X.
We have
| M¢¢
= M¢¢ ÄA |
Taking
into account (4.5), we have that ![]() , where Mi is
an Oi-module
and M0 is a T-module.
Then
, where Mi is
an Oi-module
and M0 is a T-module.
Then
| M ÄA |
| M¢¢
= (M ÄA |
By [14, Lemma 2], there is an injective
torsion-free Oi-module for each i = 1, ..., k. Therefore, the mapping ![]() with
with ![]() for each d Î D is
a monomorphism, i.e. exact sequences of Oi -modules
exist:
for each d Î D is
a monomorphism, i.e. exact sequences of Oi -modules
exist:
| 0 ® |
Since D
is injective, these sequences split, i.e. ![]() for i = 1, ..., k. Therefore,
for i = 1, ..., k. Therefore,
| M¢¢
= |
Now suppose that the ring A is of
bounded representation type and the ring ![]() is of infinite representation type. Then for any N > 0
there is an indecomposable finitely generated
is of infinite representation type. Then for any N > 0
there is an indecomposable finitely generated ![]() -module
M such that l(M) > N.
-module
M such that l(M) > N.
Consider the A-module M¢. It is finitely generated and, by [15, Proposition 1], it decomposes into a direct sum of finitely generated indecomposable A-modules:
| M¢ = N1 Å … Å Nt. |
Then
Since M¢¢ = M Å X, and M¢¢
is a finitely generated module over an Artinian ring ![]() ,
it follows from the uniqueness of the decomposition that there is a number i
such that M is a direct summand of
,
it follows from the uniqueness of the decomposition that there is a number i
such that M is a direct summand of ![]() ,
i.e. there is an
,
i.e. there is an ![]() -module P such that
-module P such that
![]() = M Å P. We have the chain of inequalities
= M Å P. We have the chain of inequalities
| mA(Ni) = |
which contradicts the assumption that A is of bounded representation type.
5. Conclusions
The problem of describing representations of
(D,O)-species has been reduced to some flat matrix problems over
discrete valuation rings with common skew field of fractions. The main matrix
problem for description of (D,O)-species of bounded representation
type is given. We establish the connection of (D,O)-species of
bounded representation type with D-species of finite representation
type. We prove that if W is a weak simply connected (D,O)-species of bounded
representation type, then the corresponding D-species ![]() is of finite representation type.
is of finite representation type.
References
[1] Gubareni N., O-species and tensor algebras, Journal of Applied Mathematics and Computational Mechanics 2016, 2(14).
[2] Gabriel P., Indecomposable representations I, Manuscripta Math. 1972, 6, 71-103.
[3] Drozd Yu.A., The structure of hereditary rings (in Russian), Mat. Sbornik 1980, 113(155), N.1(9), 161-172. English translation: Math. USSR Sbornik 1982, 41(1), 139-148.
[4] Zavadskij A.G., Revitskaya U.S., A matrix problem over a discrete valuation rings, Mat. Sb. 1999, 190(6), 835-858.
[5] Gubareni N.M., Semiperfect right hereditary rings of module representation type, Preprint 78.1, Academy of Sciences of USSR, IM, Kiev 1978 (in Russian).
[6] Gubareni N.M., Right hereditary rings of bounded representation type, Preprint-148 Inst. Electrodynamics Akad. Nauk Ukrain. SSR, Kiev 1977 (in Russian).
[7] Zavadskij A.G., Kirichenko V.V., Torsion-free modules over primary rings, Zap. Nauchn. Sem. LOMI 1976, 57, 100-116 (in Russian). English translation: J. Soviet Math. 1979, 11, 598-612.
[8] Zavadskij A.G., Kirichenko V.V., Semimaximal rings of finite type, Mat. Sb. 1977, 103, 323-345.
[9] Gubareni N., Some mixed matrix problems over several discrete valuation rings, Journal of Applied Mathematics and Computational Mechanics 2013, 4(12), 47-58.
[10] Hazewinkel M., Gubareni N., Kirichenko V.V., Algebras, Rings and Modules. Vol. 1, Mathematics and Its Applications, v.575, Kluwer Academic Publisher, Dordrecht/Boston/London 2004.
[11] Hazewinkel M., Gubareni N., Kirichenko V.V., Algebras, Rings and Modules. Vol. 2, Springer, 2007.
[12] Roiter A.V., Unbounded dimensionality of indecomposable representations of an algebra with an infinite number of indecomposable representations of an algebra with an infinite number of indecomposable representations, Math. USSR Izv. 1968, 2(6), 1223-1230.
[13] Auslander M., Representation theory of Artin algebras II, Comm. Algebra 1974, 1, 269-310.
[14] Gubareni N., Structure of finitely generated modules over right hereditary SPSD-rings, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 45-55.
[15] Rowen L.H., Finitely presented modules over semiperfect rings, Proc. Amer. Math. Soc. 1986, 97(1), 1-7.


